
4.甲、乙、丙三名射箭运动员在某次测试中各射箭20次,三人的测试成绩如下表
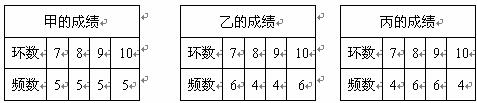
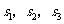 分别表示甲、乙、丙三名运动员这次测试成绩的标准差,则有(
)
分别表示甲、乙、丙三名运动员这次测试成绩的标准差,则有(
)
A.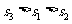 B.
B.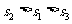 C.
C.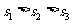 D.
D.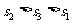
3.一袋中装有大小相同,编号分别为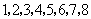 的八个球,从中有放回地每次取一个球,共取2次,则取得两个球的编号和不小于15的概率为( )
的八个球,从中有放回地每次取一个球,共取2次,则取得两个球的编号和不小于15的概率为( )
A.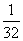 B.
B. C.
C.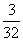 D.
D.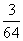
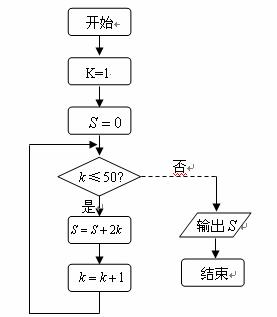
2.如果执行下面的程序框图,那么输出的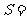 ( )
( )
A.2450 B.2500 C.2550 D.2652
1.命题“若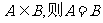 ”与其逆命题、否命题、逆否命题者四个命题中,真命题的个数是
( )
”与其逆命题、否命题、逆否命题者四个命题中,真命题的个数是
( )
A.0 B.2 C.3 D.4
22.(本小题满分12分)
设 图像上任意二点,且
图像上任意二点,且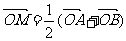 ,已知点M的纵坐标为
,已知点M的纵坐标为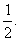
(1)求证:M点的坐标为定值;
(2)定义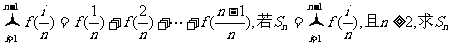 ;
;
(3)若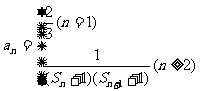 ,是否存在实数λ,对于任意n∈N*,都有
,是否存在实数λ,对于任意n∈N*,都有
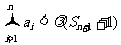 恒成立,若存在求出λ,不存在说明理由.
恒成立,若存在求出λ,不存在说明理由.
21.(本小题满分12分)
已知函数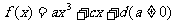 是R上的奇函数,当
是R上的奇函数,当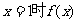 取得极值-2.
取得极值-2.
(1)求f(x)的单调区间和极大值;
(2)证明对任意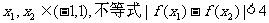 恒成立.
恒成立.
20.(本小题满分12分)
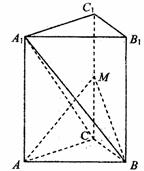 如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,CB=1,
如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,CB=1, 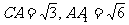 ,M为侧棱CC1上一点,AM⊥BA1.
,M为侧棱CC1上一点,AM⊥BA1.
(1)求证:AM⊥平面A1BC;
(2)求二面角B – AM – C的大小;
(3)求点C到平面ABM的距离.
19.(本小题满分12分)
甲乙两个盒子中装有大小相同的小球,甲盒中有2个黑球和2个红球,乙盒中有2个黑球和3个红球,从甲乙两盒中各任取一球交换.
(1)求交换后甲盒中恰有2个黑球的概率;
(2)求交换后甲盒中的黑球数没有减少的概率.
18.(本小题满分12分)
设不等式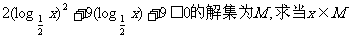 时函数
时函数
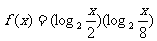 的最大值和最小值.
的最大值和最小值.
17.(本小题满分10分)
已知集合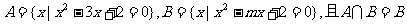 ,求实数m的取值范围.
,求实数m的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com