
4.已知数列{an}满足a1 =0,an+1 = an+2n,那么a2005的值是 ( )
A.2003×2004 B.2004×200 C.20052 D.2005×2006
3.将函数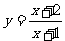 的图象按向量
的图象按向量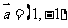 平移后所得图象的函数解析式为 ( )
平移后所得图象的函数解析式为 ( )
A.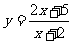 B.
B.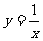 C.
C.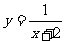 D.
D.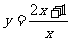
2.函数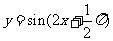 的图像的一条对称轴是
( )
的图像的一条对称轴是
( )
A.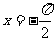 B.
B.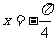 C.
C.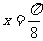 D.
D.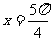
1.下列函数中既是奇函数,又在区间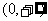 上单调递增的是 ( )
上单调递增的是 ( )
A.y=sinx B. C.
C.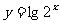 D.
D.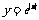
22.已知数列{an},{bn}中,a1=t(t>0且t≠1),a2=t2,且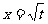 是函数
是函数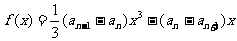 的一个极值点
的一个极值点
(1)求数列{an}的通项公式;
(2)若点Pn的坐标为(1,bn)(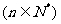 ,过函数
,过函数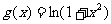 图像上的点
图像上的点
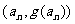 的切线始终与
的切线始终与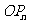 平行(O为原点),求证:当
平行(O为原点),求证:当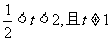 时,不等式
时,不等式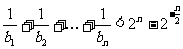 对任意
对任意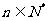 都成立
都成立
21.设a>0,函数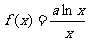
(1)讨论f(x)的单调性;
(2)求f(x)在区间[a,2a]上的最小值.
20.对于某些正整数n,存在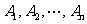 为集合{1,2,……,n}的n个不同子集,满足下列条件:对任意不大于n的正整数i,j,①
为集合{1,2,……,n}的n个不同子集,满足下列条件:对任意不大于n的正整数i,j,①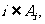 且每个
且每个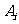 至少含有四个元素;②
至少含有四个元素;②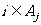 的充要条件是
的充要条件是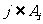 (其中
(其中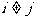 )。为了表示这些子集,作n行n列的数表,规定第i行第j列的数为
)。为了表示这些子集,作n行n列的数表,规定第i行第j列的数为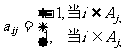
(1)求该数表中每列至多有多少个-1。
(2)用n表示该数表中1的个数,并证明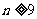
(3)请构造出集合{1,2,……,9}的9个不同子集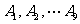 ,使得
,使得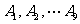 满足题设(写出一种答案即可)。
满足题设(写出一种答案即可)。
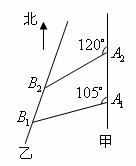
19.如图,甲船以每小时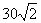 海里的速度向正北方航行,乙船按固定方向匀速直线航行,当甲船位于
海里的速度向正北方航行,乙船按固定方向匀速直线航行,当甲船位于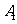 处时,乙船位于甲船的北偏西
处时,乙船位于甲船的北偏西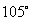 方向的
方向的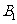 处,此时两船相距
处,此时两船相距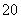 海里,当甲船航行
海里,当甲船航行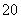 分钟到达
分钟到达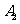 处时,乙船航行到甲船的北偏西
处时,乙船航行到甲船的北偏西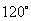 方向的
方向的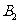 处,此时两船相距
处,此时两船相距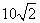 海里,问乙船每小时航行多少海里?
海里,问乙船每小时航行多少海里?
18.(本小题满分12分)在直角坐标系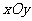 中,以
中,以 为圆心的圆与直线
为圆心的圆与直线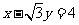 相切.
相切.
(1)求圆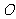 的方程;
的方程;
(2)圆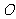 与
与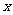 轴相交于
轴相交于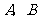 两点,圆内的动点
两点,圆内的动点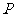 使
使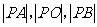 成等比数列,求
成等比数列,求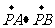 的取值范围.
的取值范围.
17.已知函数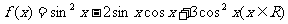
(1)说明函数y=f(x)图像可由y=cos2x的图像经过怎样的变换得到;
(2)当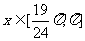 时,求函数f(x)的最大值和最小值
时,求函数f(x)的最大值和最小值
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com