
3.首项为-24的等差数列,从第10项开始为正,则公差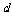 的取值范围是 ( )
的取值范围是 ( )
A.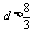 B.
B.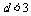 C.
C.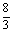 ≤
≤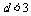 D.
D.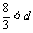 ≤3
≤3
2.已知抛物线y= x2,则它的焦点坐标是 ( )
A.(0,) B.( ,0) C.(,0) D.(0, )
1.已知集合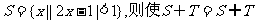 的集合T= ( )
的集合T= ( )
A.{x|0<x<1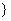 B.
B.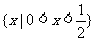 C.
C.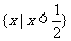 D.
D.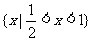
22.(本小题满分12分)
已知椭圆的一个顶点为A(0,-1),焦点在x轴上.若右焦点到直线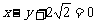 的距离为3.
的距离为3.
(1)求椭圆的方程;
(2)设椭圆与直线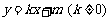 相交于不同的两点M、N.当
相交于不同的两点M、N.当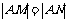 时,求m的取值范围.
时,求m的取值范围.
21.(本小题满分14分)
已知向量i=(1,0),j=(0,1),函数f(x)=ax4+bx2+c(a≠0,a≠c)的图象在y轴上的截距为1,在x=2处切线的方向向量为(a-c)i-12bj,并且函数当x=1时取得极值。
(1)求f(x)的解析式;
(2)求f(x)的单调递增区间和极值.
20.(本小题满分14分)
如图所示,△ABC为正三角形,EC⊥平面ABC,BD∥CE,且CE=CA=2BD=4,
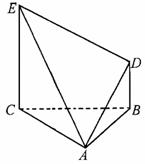
(1)求证:△AED为等腰三角形;
(2)求:异面直线DE与CA所成的角;
(3)求:二面角A-ED-B的大小.
19.(本小题满分12分)
已知点A(2,8),B(x1,y1),C(x2,y2)在抛物线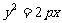 上,△ABC的重心与此抛物线的焦点F重合(如图)
上,△ABC的重心与此抛物线的焦点F重合(如图)
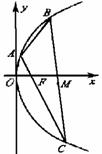
(1)写出该抛物线的方程和焦点F的坐标;
(2)求线段BC中点M的坐标;
(3)求BC所在直线的方程.
18.(本小题满分12分)( 请同学们注意:此题求证方法只能应用几何法推证,不能使用坐标解析法,否则不得分. )
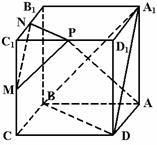
如图所示,在正方体ABCD-A1B1C1D1中,M、N、P分别是C1C、B1C1、C1D1的中点,求证:
(1)AP⊥MN
(2)平面MNP∥平面A1BD.
17.(本小题10分)
已知等差数列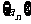 的前n项和为
的前n项和为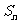 ,公差
,公差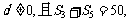
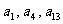 成等比数列。
成等比数列。
(1)求数列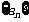 的通项公式;
的通项公式;
(2)若从数列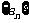 中依次取出第2项、第4项、第8项,
中依次取出第2项、第4项、第8项,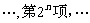 ,按原来顺序组成一个新数列
,按原来顺序组成一个新数列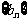 ,且这个数列的前
,且这个数列的前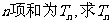 的表达式;
的表达式;
16.已知m、n是直线,α、β、γ是平面,给出下列命题:
①若α⊥β,α∩β=m , n⊥m , 则n⊥α或n⊥β;
②若α∥β,α∩γ=m ,β∩γ=n , 则m∥n ;
③若m不垂直于α,则m不可能垂直于α内的无数条直线 ;
④若α∩β=m , n∥m
, 且n β, n
β, n α,则n∥α且n∥β.
其中正确的命题序号是
.(注:把你认为正确命题的序号都填上)
α,则n∥α且n∥β.
其中正确的命题序号是
.(注:把你认为正确命题的序号都填上)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com