
22.(14分)已知函数
(I)求f(x)在[0,1]上的极值;
(II)若对任意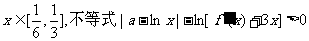 成立,求实数a的取值范围;
成立,求实数a的取值范围;
(III)若关于x的方程 在[0,1]上恰有两个不同的实根,求实数b的取值范围.
在[0,1]上恰有两个不同的实根,求实数b的取值范围.
21.(12分)数列 的前
的前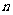 项和记作
项和记作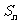 ,满足
,满足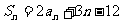 ,
,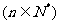
(1)证明数列 为等比数列;并求出数列
为等比数列;并求出数列 的通项公式.
的通项公式.
(2)记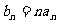 ,数列
,数列 的前
的前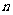 项和为
项和为 ,求
,求 .
.
20.(12分)已知函数 ,
,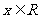 .
. 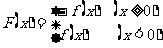
(1)若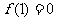 ,且函数
,且函数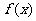 的值域为
的值域为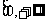 ,求
,求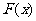 的表达式;
的表达式;
(2)在(1)的条件下,当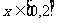 时,
时,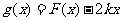 是单调函数,求实数
是单调函数,求实数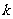 的取值范围.
的取值范围.
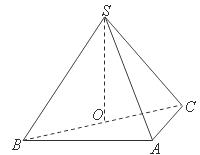
19.(12分) 如图,在三棱锥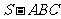 中,侧面
中,侧面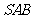 与侧面
与侧面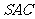 均为等边三角形,
均为等边三角形,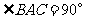 ,
, 为
为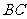 中点.
中点.
(Ⅰ)证明: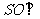 平面
平面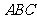 ;
;
(Ⅱ)求二面角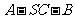 的余弦值.
的余弦值.
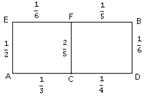
18.(12分)某人居住在A处,准备开车到B处上班.若各路段发生堵车都是相互独立的,同一路段发生堵车最多只有一次,发生堵车的概率如图(例如: 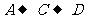 算作两段:路段AC发生堵车的概率为
算作两段:路段AC发生堵车的概率为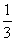 ,
路段CD发生堵车的概率为
,
路段CD发生堵车的概率为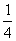 ).
).
(1)请你为其选择一条由A到B的路线,使不堵车的概率最大;
(2)求路线 中遇到堵车次数的期望.
中遇到堵车次数的期望.
17.(12分)已知集合A=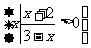 ,B=
,B=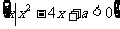 , 若AÇB=B,求a的取值范围.
, 若AÇB=B,求a的取值范围.
16.关于x的方程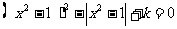 给出下列四个命题:
给出下列四个命题:
①存在实数k,使方程恰好有2个不同的实数根;
②存在实数k,使方程恰好有4个不同的实数根;
③存在实数k,使方程恰好有5个不同的实数根;
④存在实数k,使方程恰好有8个不同的实数根;
其中是真命题的有 .(填序号)
15.已知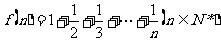 用数学归纳法证明不等式
用数学归纳法证明不等式
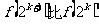 多的项数是
.
多的项数是
.
14.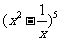 展开式中
展开式中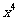 的系数是
.(用数字作答)
的系数是
.(用数字作答)
13.函数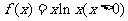 的单调递增区间是 .
的单调递增区间是 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com