
3.(由第一册§2.9练习第3、4题整合改编)一种产品的年产量原来是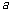 件,计划在今后
件,计划在今后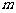 年内,使年产量平均每年比上一年增长
年内,使年产量平均每年比上一年增长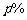 ,在计划内年产量随年数变化的函数关系是( )
,在计划内年产量随年数变化的函数关系是( )
A.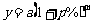 B.
B.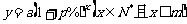
C.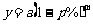 D.
D.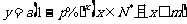
2.(由第一册复习参考题二A组第13(1)题改编)函数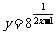 的值域是( )
的值域是( )
A.R B. C.
C.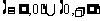 D.
D.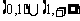
1.(由第一册§1.3例3改编)设集合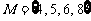 ,
,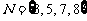 ,
,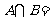 ( )
( )
A.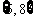 B.
B. C.
C. D.
D.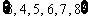
21.(本小题满分18分)
求证:只要二次函数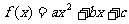 满足条件:①
满足条件:① ;②
;②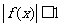 ,
,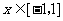 ;③
;③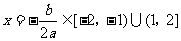 ,就有
,就有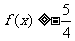 ,
,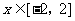 ,并求出这样的二次函数
,并求出这样的二次函数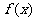 ,使
,使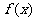 在[-2,2]上的最小值为
在[-2,2]上的最小值为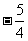 。
。
20.(本小题满分16分)
已知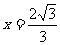 是函数
是函数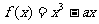 的一个极值点。
的一个极值点。
(1)求实数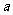 的值;
的值;
(2)若数列{ }满足:
}满足: ,且
,且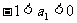 。试问
。试问 与
与 的大小关系是否确定?若是,请加以证明;若不是,说明理由。
的大小关系是否确定?若是,请加以证明;若不是,说明理由。
19.(本小题满分16分)
如下图,在正方体ABCD-A1B1C1D1中,E、F分别是BB1、CD的中点。
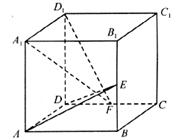
(1)证明:AD⊥D1F;
(2)求AE与D1F所成的角;
(3)证明:平面AED⊥平面A1D1F。
18.(本小题满分16分)
袋子A和B中装有若干个均匀的红球和白球,从A中摸出一个红球的概率是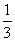 ,从B中摸出一个红球的概率为
,从B中摸出一个红球的概率为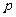 。
。
(1)从A中有放回地摸球,每次摸出一个,有3次摸到红球即停止。
①求恰好摸5次停止的概率;
②记5次之内(含5次)摸到红球的次数为 ,求随机变量
,求随机变量 的分布率及数学期望
的分布率及数学期望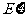 。
。
(2)若A、B两个袋子中的球数之比为1︰2,将A、B中的球装在一起后,从中摸出一个红球的概率是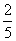 ,求
,求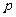 的值。
的值。
17.(本小题满分14分)
将圆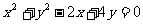 按向量
按向量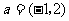 平移后得到⊙O,直线
平移后得到⊙O,直线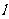 与⊙O相交于A、B两点,若在⊙O上存在一点C,使
与⊙O相交于A、B两点,若在⊙O上存在一点C,使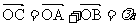 ,求直线
,求直线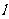 的方程及对应的点C的坐标。
的方程及对应的点C的坐标。
16.设 与
与 ,
,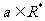 ,是直角坐标平面
,是直角坐标平面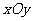 内的点集,则
内的点集,则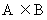 A∈B的充要条件是
A∈B的充要条件是
A. B.
B.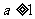 C.
C.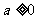 D.
D.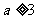
15.已知: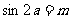 ,
,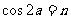 ,
,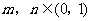 ,则
,则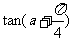 的4个答案:
的4个答案:
①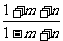 ; ②
; ② ; ③
; ③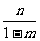 ;④
;④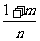 中,正确的个数为
中,正确的个数为
A.0个 B.2个 C.3个 D.4个
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com