
2.若函数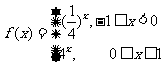 ,则
,则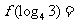 ( )
( )
A.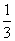 B.
B.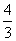 C.
C.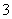 D.
D.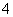
1.已知集合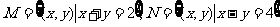 ,那么集合
,那么集合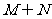 为( )
为( )
A.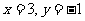 B.
B.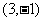 C.
C.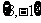 D.
D.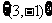
22.(本小题满分14分)
已知椭圆E: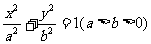 的离心率为
的离心率为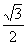 ,双曲线E’:
,双曲线E’: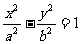 的焦距为
的焦距为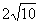 ,直线
,直线 :
: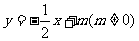 与椭圆E相交于A、B两个不同点.
与椭圆E相交于A、B两个不同点.
(Ⅰ)求椭圆E的方程;
(Ⅱ)求m的取值范围;
(Ⅲ)椭圆E上是否存在这样的点M,使得直线MA、MB与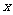 轴始终围成一个底边在
轴始终围成一个底边在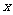 轴上的等腰三角形,若存在,求出所有的M点的坐标;若不存在,说明理由.
轴上的等腰三角形,若存在,求出所有的M点的坐标;若不存在,说明理由.
21.(本小题满分12分)
已知定义在(0,+∞)上的函数 ,
,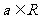 .
.
(Ⅰ)求函数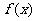 的单调区间;
的单调区间;
(Ⅱ)当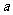 >0时,求函数
>0时,求函数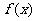 在区间(0,4]上的最小值.
在区间(0,4]上的最小值.
20.(本小题满分12分)
已知数列{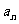 }的前n项和Sn和通项
}的前n项和Sn和通项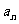 之间满足关系
之间满足关系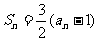 .
.
(Ⅰ)求数列{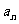 }的通项公式;
}的通项公式;
(Ⅱ)设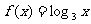 ,
,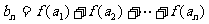 ,
,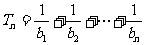 ,求
,求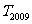 .
.
19.(本小题满分12分)
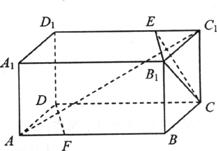
如图,长方体ABCD-AlBlClDl中,AB=2AAl=2AD,点E在ClDl上,点F在AB上,ClE=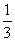 EDl,AF=
EDl,AF=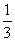 FB.
FB.
(I)证明:DF//平面EB1C;
(II)证明:AC1⊥平面EB1C.
18.(本小题满分12分)
在△ABC中,有sin2C=sin2A+sin2B-sinAsinB.
(Ⅰ)求角C;
(Ⅱ)若△ABC长为y,角B等于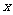 ,AB=3,求函数
,AB=3,求函数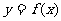 的最大值.
的最大值.
17.(本小题满分l2分)
在甲、乙两个盒子中分别装有编号为l,2,3,4的四个小球,现从甲、乙两个盒子中各取出1个小球,每个小球被取出的可能性相等.
(Ⅰ)求取出的两个球上的编号都为奇数的概率;
(Ⅱ)求取出的两个球上的编号之和为3的倍数的概率;
(Ⅲ)求取出的两个球上的编号之和大于6的概率.
16.已知函数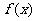 的值域为(0,3],则能使不等式-2+m<
的值域为(0,3],则能使不等式-2+m<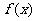 <2+m恒成立的实数m的取值范围是_________.
<2+m恒成立的实数m的取值范围是_________.
15.棱长为2的正四面体的内切球的体积是_________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com