
20.(本题满分16分)
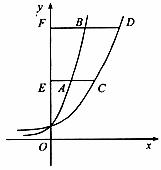
如图,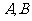 AM是函数
AM是函数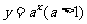 在
在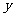 轴右侧图像上的两点,分别过
轴右侧图像上的两点,分别过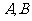 作
作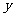 轴的垂线与
轴的垂线与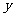 轴交于
轴交于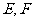 两点,与函数
两点,与函数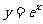 的图像交于
的图像交于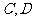 两点,且
两点,且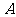 是
是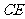 的中点。
的中点。
(I)求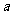 的值;
的值;
(II)当直线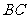 与
与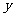 轴平行时,设
轴平行时,设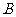 点的横坐标为
点的横坐标为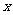 ,四边形
,四边形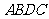 的面积为
的面积为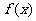 ,求
,求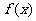 的解析式;
的解析式;
(III)若对任意的正数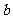 ,关于
,关于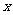 的不等式
的不等式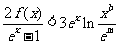 在区间
在区间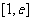 上恒成立,求实数
上恒成立,求实数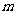 的取值范围。
的取值范围。
19.(本题满分16分)
设函数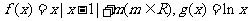
(I)记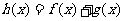 ,求证:
,求证: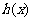 在区间(0,1)上是增函数;
在区间(0,1)上是增函数;
(II)若方程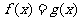 有解,求
有解,求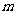 的取值范围。
的取值范围。
18.(本题满分15分)
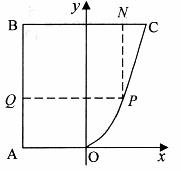
某地方政府为科技兴市,欲将如图所示的一块不规则的非农业用地规划建成一个矩形的高科技工业园区,已知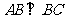 ,
,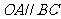 ,且
,且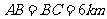 ,
,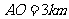 ,曲线段
,曲线段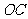 是二次函数
是二次函数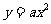 图像的一段,如果要使矩形的相邻两边分别落在
图像的一段,如果要使矩形的相邻两边分别落在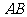 ,
,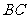 上,且一个顶点落在曲线段
上,且一个顶点落在曲线段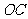 上,问应如何规划才能使矩形工业园区
上,问应如何规划才能使矩形工业园区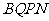 的用地面积最大?并求出最大的用地面积。
的用地面积最大?并求出最大的用地面积。
17.(本题满分15分)
已知函数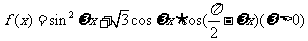 ,其图像相邻两对称轴之间的距离为
,其图像相邻两对称轴之间的距离为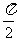
(I)求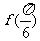 的值;
的值;
(II)若函数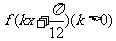 在区间
在区间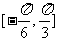 上单调递增,试求
上单调递增,试求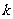 的最大值。
的最大值。
16.(本题满分14分)
已知命题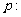 函数
函数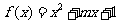 有两个不相同的零点且为负数;命题
有两个不相同的零点且为负数;命题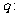 关于
关于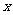 的方程
的方程 没有实数根
没有实数根
(I)求实数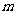 的取值范围,使命题
的取值范围,使命题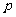 为真命题;
为真命题;
(II)若“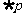 或
或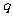 ”为真命题,“
”为真命题,“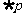 且
且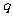 ”为假命题,求实数
”为假命题,求实数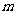 值的集合。
值的集合。
15.(本题满分14分)
已知在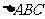 中,
中,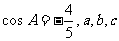 分别是角
分别是角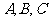 所对的边
所对的边
(I)若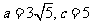 ,求
,求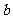 ;
;
(II)若 ,求
,求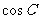 的值。
的值。
14.设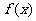 是定于在
是定于在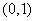 上的函数,且满足:①对任意
上的函数,且满足:①对任意 ,恒有
,恒有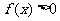 ;②对任意
;②对任意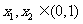 ,恒有
,恒有 ,则关于函数
,则关于函数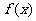 有:
有:
(1)对任意 ,都有
,都有 ;(2)对任意
;(2)对任意 ,都有
,都有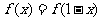 ;
;
(3)对任意 ,恒有
,恒有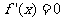 ;(4)当
;(4)当 ,函数
,函数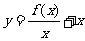 为减函数。
为减函数。
上述四个命题中正确的有________________。
13.函数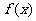 满足
满足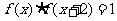 ,若
,若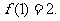 则
则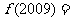 ___________。
___________。
12.已知函数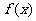 是定义在
是定义在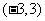 上的奇函数,当
上的奇函数,当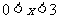 时,
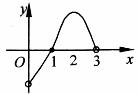
时,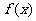 的图象如图所示,则不等式
的图象如图所示,则不等式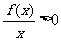 的解集是_________。
的解集是_________。
11.若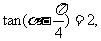 则
则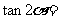 _____________。
_____________。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com