
21.(本题满分12分)
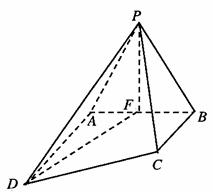
如图,四棱锥P-ABCD中,底面ABCD是直角梯形,∠ABC=90°,AD//BC,CB⊥侧面PAB,△PAB是等边三角形,BC=1,DA=AB=2BC,F是线段AB的中点。
(1)求证:DF⊥PF;
(2)求PC与平面PDF所成的角。
20.(本题满分12分)
双曲线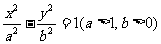 的焦距为2c,直线
的焦距为2c,直线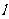 过点(a,0)和(0,b),点(1,0)到直线
过点(a,0)和(0,b),点(1,0)到直线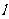 的距离为m,点(-1,0)到直线
的距离为m,点(-1,0)到直线 的距离为n,设m+n的和为s且
的距离为n,设m+n的和为s且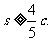
(1)用含有a,b的式子表示s ;
(2)求双曲线的离心率e的取值范围.
19.(本题满分12分)
已知圆的方程x2+y2=25,点A为该圆上的动点,AB与x轴垂直,B为垂足,点P分有向线段BA的比λ=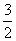 .
.
(1)求点P的轨迹方程并化为标准方程形式;
(2)写出轨迹的焦点坐标和准线方程.
18.(本题满分12分)
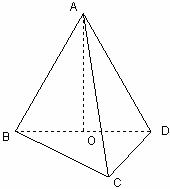
如图,在三棱锥A-BCD中,侧面ABD是边长为1的正三角形,O为BD的中点,底面BCD满足BC=CD,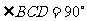 ,且侧面
,且侧面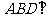 底面
底面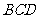
(I)求证: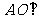 平面
平面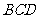 ;
;
(II)求二面角A-BC-D的平面角的正切值;
17.(本题满分10分)
如图,在正三棱柱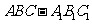 中,
中,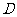 是侧棱
是侧棱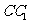 的中点,
的中点,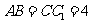
(1)求证: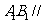 面
面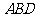 ;
;
(2)求二面角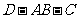 的大小。
的大小。

16.将正方形ABCD沿对角线BD折成直二面角A-BD-C,有如下四个结论:
①AC⊥BD; ②△ACD是等边三角形;
③AB与平面BCD所成的角为60° ④AB与CD所成的角为60°
其中正确结论的序号是 ____________ .(写出所有你认为正确的结论的序号)
15.已知正四棱柱的对角线的长为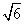 ,且对角线与底面所成角的余弦值为
,且对角线与底面所成角的余弦值为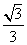 ,则该正四棱柱的体积等于_________.
,则该正四棱柱的体积等于_________.
|
14.已知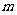 、
、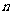 是直线,
是直线,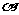 、
、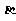 、
、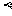 是平面,给出下列命题:
是平面,给出下列命题:
①
若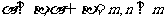 ,则
,则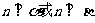 ;
;
②若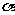 ∥
∥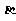 ,
,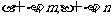 ,则
,则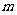 ∥
∥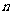 ;
;
③若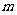 不垂直于
不垂直于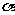 ,则
,则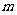 不可能垂直于
不可能垂直于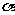 内的无数条直线;
内的无数条直线;
④若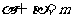 ,
,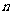 ∥
∥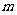 ,且
,且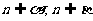 ,则
,则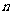 ∥
∥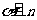 ∥
∥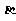 .
.
其中正确的命题的序号是_________________(注:把你认为正确的命题的序号都填上)
13.抛物线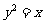 的准线方程是
.
的准线方程是
.
12.若椭圆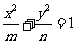 (m>n>0)与双曲线
(m>n>0)与双曲线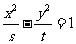 (s>0, t>0)有相同的焦点F1和F2
(s>0, t>0)有相同的焦点F1和F2
(m≠s),P是两曲线的一个公共点,则|PF1|·|PF2|的值是 ( )
A.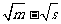 B.m-s C.
B.m-s C.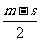 D.
D.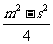
第Ⅱ卷 非选择题(共90分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com