
17.(12分)已知函数f (x) =
2cos2x +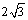 sinxcosx.
sinxcosx.
(1)求函数f
(x)定义在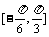 上的值域;
上的值域;
(2)在△ABC中,若f (C) = 2, 2sinB = cos(A – C) – cos(A + C),求tanA的值.
16.(12分)6个大小相同的小球分别标有数字1,1,1,2,2,2,把它们放在一个盒子里,从中任意摸出两个小球,它们所标有的数字分别为x,y,记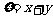 .
.
(1)求随机变量 分布列及数学期望;
分布列及数学期望;
(2)设“函数f
(x)=x2– x–1在区间(2,
3)上有且只有一个零点”为事件A,求事件A发生的概率.
x–1在区间(2,
3)上有且只有一个零点”为事件A,求事件A发生的概率.
14.已知m、n是两条不重合的直线,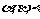 是三个互不重合的平面,给出下列命题
是三个互不重合的平面,给出下列命题
①若m∥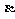 ,n∥
,n∥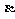 ,m,n
,m,n
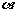 ,则
,则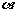 ∥
∥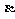
②若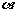 ⊥
⊥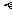 ,
,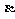 ⊥
⊥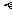 ,
,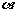 ∩
∩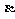 = m,n
= m,n
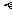 ,则m⊥n
,则m⊥n
③若m⊥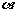 ,
,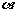 ⊥
⊥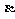 ,m∥n,则n∥
,m∥n,则n∥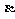
④若n∥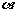 ,n∥
,n∥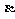 ,
,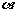 ∩
∩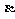 = m,那么m∥n
= m,那么m∥n
其中正确命题的序号是 .
|
|
|
|
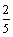 ,出现1的概率为
,出现1的概率为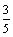 ,记
,记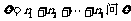 = 4时的概率为 ,
= 4时的概率为 , 的数学期望是 .
的数学期望是 .13.在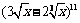 的展开式中任取一项,设所取项为有理项的概率为
的展开式中任取一项,设所取项为有理项的概率为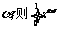 dx = .
dx = .
12.若不等式x2 + |2x – 6|≥a对于一切实数x均成立,则实数a的最大值是 .
11.若关于x,y的不等式组 表示的平面区域是一个三角形,则a的取值范围是 .
表示的平面区域是一个三角形,则a的取值范围是 .
10.正方体ABCD-A1B1C1D1的棱长为1,E是A1B1的中点,则点E到平面ABC1D1的距离是 .
9.直线l1:y = mx + 1,直线l2的方向向量为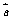 = (1,2),且l1⊥l2,则m
= .
= (1,2),且l1⊥l2,则m
= .
8.设函数y=f(x)是定义域为R的奇函数,且满足f(x–2)=–f(x)对一切x∈R恒成立,当–1≤x≤1时,f(x)=x3,则下列四个命题:①f(x)是以4为周期的周期函数;②f(x)在[1,3]上的解析式为f(x)=(2–x)3;③f(x)在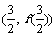 处的切线方程为3x+4y–5=0;④f(x)的图象的对称轴中,有x=±1,其中正确的命题是 ( )
处的切线方程为3x+4y–5=0;④f(x)的图象的对称轴中,有x=±1,其中正确的命题是 ( )
A.①②③ B.②③④ C.①③④ D.①②③④
7.①点P在△ABC所在的平面内,且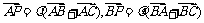 ;②点P为△ABC内的一点,且使得
;②点P为△ABC内的一点,且使得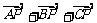 取得最小值;③点P是△ABC所在平面内一点,且
取得最小值;③点P是△ABC所在平面内一点,且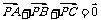 ,上述三个点P中,是△ABC的重心的有 ( )
,上述三个点P中,是△ABC的重心的有 ( )
A.0个 B.1个 C.2个 D.3个
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com