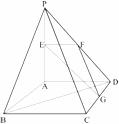
16．(本小题满分12分)如图，，ABCD为正方形，且PA=AD=2，E、F、G分别是线段PA、PD、CD的中点.

　 (1)求异面直线EG与BD所成的角；

　 (2)求A点到平面EFG的距离。

15．已知变量x、y满足约束条件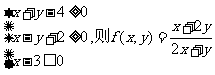的范围是______________.

14．如图，ABCD-A₁B₁C₁D₁为正方体，下面结论中正确的结论是__________________，(把你认为正确的结论都填上。)

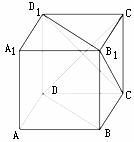
①BD//平面CB₁D₁；　　　　　　 　　　　　　　 ②AC₁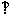平面CB₁D₁；

③AC₁与底面ABCD所成的角的正切值是；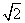

④二面角C-B₁D₁-C₁的正切值是.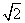

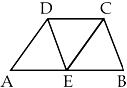
13．如图，在等腰梯形ABCD中，AB＝2DC＝2，DAB=60，E为AB的中点，将△AED与△BEC分别沿ED、EC向上折起，使A、B重合于点P，则三棱锥P-DCE的外接球的体积为：＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿.

12．已知抛物线型拱桥的顶点距离水面2米时，测量水面宽为8米，当水面上升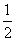米后，水面的宽度是＿＿＿＿＿＿＿＿＿＿＿＿＿＿.

11．设双曲线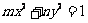的一个焦点与抛物线的焦点相同，离心率为2，则此双曲线的渐近线方程为_______________________________.

10．已知椭圆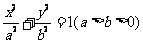和双曲线有相同的焦点F₁、F₂,以线段F₁、F₂为边作正三角形F₁F₂M，若椭圆与双曲线的一个交点P恰好是MF₁的中点，设椭圆和双曲线的离心率分别为e₁和e₂，则e₁·e₂等于(　)

A．5　　　　　　　　　　　　　 B．4　　　 　　　　　　　 C．3　　　　　　　　　　　　　　 D．2

9．经过椭圆的右焦点F任意作弦AB，过A点作椭圆的右准线的垂线AM，垂足为M，则直线BM必经过点(　 　)

　 　A．(2，0)　　　　　　　　 B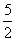．(，0)　　　　　　　 C．(3，0)　　　　　 D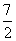．(，0)

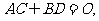
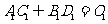8．直四棱柱ABCD-A₁B₁C₁D₁的高为3，底面是边长为4且DAB=60的菱形，，则二面角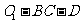的大小为( 　　)

　 　A．60　　　　　　　　　　　　 B．90　　　　　　　　 C．120　　　　　　　 　　　 D．150

7．正方体ABCD-A₁B₁C₁D₁中，O是BD的中点，M是线段AD₁上的一点，则在下列位置关系中，不可能成立的是( 　　)

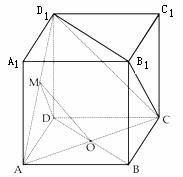
　 　　 A．OM//平面CDD₁C₁　　　　　　　　　　　　　　　 B．OM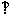BC

C．AD₁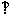平面OMD　　　　　　　　　 　　　　　　　 D．平面OMD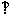平面D₁AC