
18.已知:在函数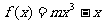 的图象上,以
的图象上,以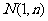 为切点的切线的倾斜角为
为切点的切线的倾斜角为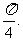
(I)求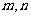 的值;
的值;
(II)是否存在最小的正整数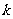 ,使得不等式
,使得不等式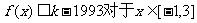 恒成立?如果存在,请求出最小的正整数
恒成立?如果存在,请求出最小的正整数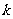 ,如果不存在,请说明理由。
,如果不存在,请说明理由。
解:(1)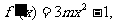
依题意,得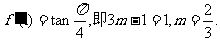
因为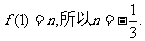 …………6分
…………6分
(II)令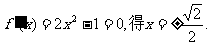 …………8分
…………8分
当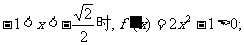
当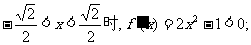
当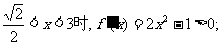
又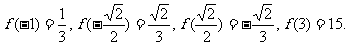
因此, 当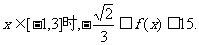 …………12分
…………12分
要使得不等式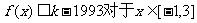 恒成立,则
恒成立,则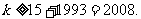
17.(本题满分14分)
已知向量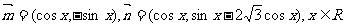 ,令
,令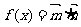 ,
,
(1)求函数f(x)的单调递增区间;
(2)当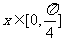 时,求函数f(x)的值域.
时,求函数f(x)的值域.
⒖解:(Ⅰ) 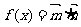
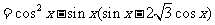
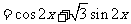
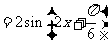 ……(4分)
……(4分)
∵函数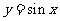 的单调增区间为
的单调增区间为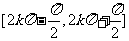 ,
,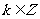
∴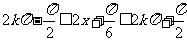 ,∴
,∴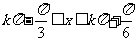 ,
,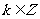
∴函数f(x)的单调递增区间为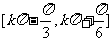 ,
,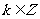 ……(8分)
……(8分)
(Ⅱ)当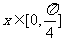 时,
时,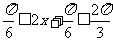 ,∴
,∴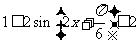
∴函数f(x)的值域为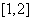 ……(14分)
……(14分)
16. (本题14分)已知函数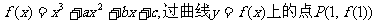 的切线方程为y=3x+1,且函数
的切线方程为y=3x+1,且函数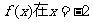 处有极值.
处有极值.
(Ⅰ)求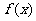 的表达式;(Ⅱ)求函数
的表达式;(Ⅱ)求函数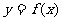 在[-3,1]上的最大值.
在[-3,1]上的最大值.
解:(1)由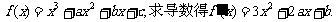
过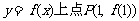 的切线方程为:
的切线方程为:
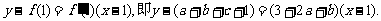 …………2分
…………2分
而过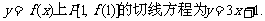
|
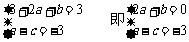 …………4分
…………4分
∵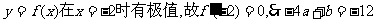 ③
③
由①②③得 a=2,b=-4,c=5.
∴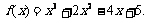
(2)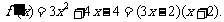
当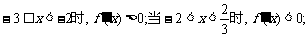
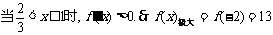
又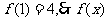 在[-3,1]上最大值是13.
在[-3,1]上最大值是13.
15.(本题14分)已知集合A={x|x2-2x-8≤0,x∈R},B={x|x2-(2m-3)x+m2-3m≤0,x∈R,m∈R }.
(Ⅰ) 若A∩B=[2,4],求实数m的值;
(Ⅱ) 设全集为R,若A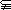 ∁RB,求实数m的取值范围.
∁RB,求实数m的取值范围.
解 由已知得A=[-2,4],B=[m-3,m].
(Ⅰ)∵A∩B=[2,4],∴∴m=5.
(Ⅱ)∵B=[m-3,m],∴∁RB=(-∞,m-3)∪(m,+∞).
∵A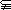 ∁RB,∴m-3>4或m<-2.∴m>7或m<-2.
∁RB,∴m-3>4或m<-2.∴m>7或m<-2.
∴m∈(-∞,-2)∪(7,+∞).
14.设函数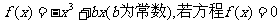 的根都在区间[-2,2]内,且函数
的根都在区间[-2,2]内,且函数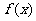 在区间(0,1)上单调递增,则b的取值范围是 [3,4]
在区间(0,1)上单调递增,则b的取值范围是 [3,4]
13.定义在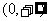 上的函数
上的函数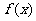 的导函数
的导函数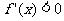 恒成立,且
恒成立,且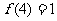 ,若
,若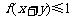 ,则
,则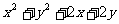 的最小值是
的最小值是 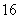
12.已知函数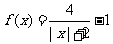 的定义域是
的定义域是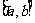 (
(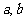 为整数),值域是
为整数),值域是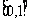 ,则满足条件的整数数对
,则满足条件的整数数对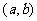 共有_________个.
共有_________个.
答案:5
11.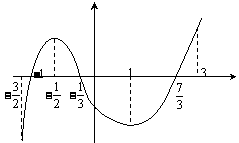 已知函数
已知函数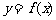 在定义域
在定义域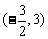 上可导,其图像如图,记
上可导,其图像如图,记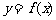 的导函数
的导函数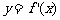 ,则不等式
,则不等式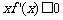 的解集是_______
的解集是_______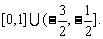 _.
_.
10.设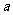 为实数,函数
为实数,函数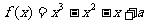 ,当
,当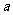 时,曲线
时,曲线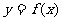 与
与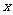 轴仅有一个交点。
轴仅有一个交点。
(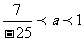 )
)
9.若函数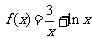 在区间
在区间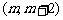 上单调递减,则实数m的范围是____
上单调递减,则实数m的范围是____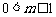 .____.
.____.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com