
例2、已知函数f(x)的定义域是(0,+∞),满足f(4)=1,f(xy)=f(x)+f(y).(1)证明f(1)=0;(2)求f(16);(3)试证f(xn)=nf(x),n∈N*.
思维分析:这显然是一个抽象函数。根据题目给定的三个条件,可以将对数函数y=log4x作为该函数的原型,从而找到问题的解决思路与方法
例1、解关于x的对数不等式;
2 loga (x-4)>loga(x-2).
思维分析:可以去掉对数符号,化为一般的代数不等式求解;同时考虑到底数a的取值范围不确定,故应进行分类讨论。
例4:若方程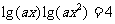 的所有解都大于1,求
的所有解都大于1,求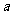 的取值范围。
的取值范围。
分析:由对数函数的性质,方程可变形为关于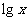 的一元二次方程,化归为一元二次方程解的讨论。
的一元二次方程,化归为一元二次方程解的讨论。
思维点拔:
(1)有关对数方程解的情况讨论,通常是利用换元法,将方程转化为一元一次或一元二次方程解的讨论;如果是方程解的个数问题,又可以用函数的图象求解,如求方程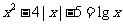 的实根的个数。
的实根的个数。
(2)换元后必须保证新变量与所替换的量的取值范围的一致性。
追踪训练二
1. 已知方程
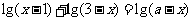
(1)若方程有且只有一个根,求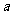 的取值范围 .
的取值范围 .
(2)若方程无实数根,求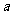 的取值范围 .
的取值范围 .
|
学生质疑 |
|
|
教师释疑 |
|
3.画出函数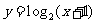 与
与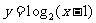 的图象,并指出这两个函数图象之间的关系。
的图象,并指出这两个函数图象之间的关系。
[选修延伸]
例4: 已知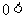
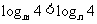 ,比较
,比较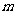 ,
,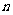 的大小。
的大小。
[分析]:由条件可得:
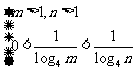 ;
;
所以,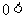
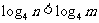 ,则
,则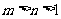 。
。
[变式]:已知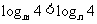 ,则
,则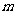 ,
,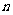 的大小又如何?
的大小又如何?
[解]∵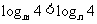 ,
,
∴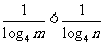 ,
,
当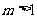 ,
,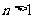 时,得
时,得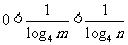 ,
,
∴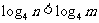 , ∴
, ∴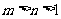 .
.
当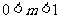 ,
,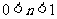 时,得
时,得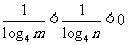 ,
,
∴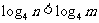 , ∴
, ∴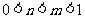 .
.
当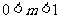 ,
,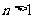 时,得
时,得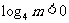 ,
,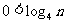 ,
,
∴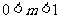 ,
,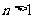 , ∴
, ∴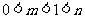 .
.
综上所述,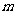 ,
,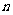 的大小关系为
的大小关系为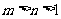 或
或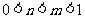 或
或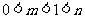
思维点拔:
对于不同底的对数式,一般的方法是转化为同底的对数式,然后再利用对数函数的单调性求解,此类题目也可以用对数函数的图象的分布特征求解。数形结合是解决函数问题的重要思想方法。
追踪训练二
1比较下列各组值的大小.
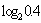 ,
,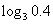 ,
,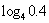
|
学生质疑 |
|
|
教师释疑 |
|
2.解下列不等式:
(1)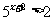 (2)
(2)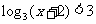
1. 比较下列各组值的大小:
(1)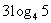 ,
,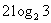 ;
;
(2)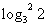 ,
,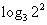 ,
,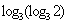 ;
;
4.说明:上述变换称为平移变换。
[精典范例]
例1:说明下列函数的图像与对数函数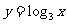 的图像的关系,并画出它们的示意图,由图像写出它的单调区间:
的图像的关系,并画出它们的示意图,由图像写出它的单调区间:
(1)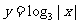 ; (2)
; (2)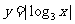 ;
;
(3) 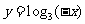 ;(4)
;(4) 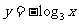
分析:由函数式出发分析它与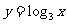 的关系,再由
的关系,再由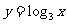 的图象作出相应函数的图象。
的图象作出相应函数的图象。
[解](1)
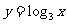
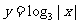
 图象(略)
图象(略)
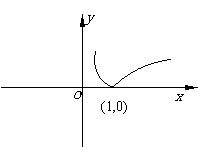
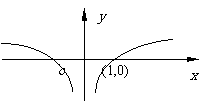
由图象知:单调增区间为 ,单调减区间为
,单调减区间为 。
。
(2)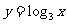
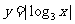
由图象知:单调增区间为 ,单调减区间为
,单调减区间为 。
。
(3)
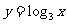
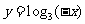
由图象知:单调减区间为 。
。
(4)
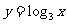
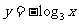
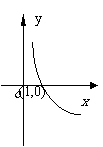
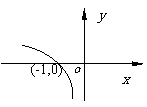 由图象知:单调减区间为
由图象知:单调减区间为 。
。
点评:
(1)上述变换称为对称变换。一般地:
① ;
;
②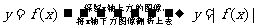 ;
;
③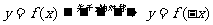 ;
;
④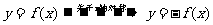
(2)练习:怎样由对数函数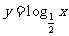 的图像得到下列函数的图像?
的图像得到下列函数的图像?
(1)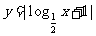 ;
;
(2)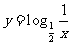 ;
;
答案:(1)由的图象先向2左平移1个单位,保留上方部分的图象,并把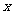 轴下方部分的图象翻折上去得到
轴下方部分的图象翻折上去得到
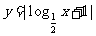 的图象。
的图象。
(2)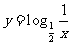 的图象是
的图象是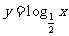 关于
关于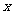 轴对称的图象。
轴对称的图象。
例2:求下列函数的定义域、值域:
(1)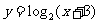 ; (2)
; (2)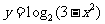 ; (3)
; (3)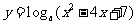 (
(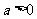 且
且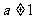 ).
).
分析:这是复合函数的值域问题,复合函数的值域的求法是在定义域的基础上,利用函数的单调性,由内而外,逐层求解。
点评: 求复合函数的值域一定要注意定义域。
例3:设f (x)=lg(ax2-2x+a),
(1) 如果f (x)的定义域是(-∞, +∞),求a的取值范围;
(2) 如果f (x)的值域是(-∞, +∞),求a的取值范围.
追踪训练一
3. 函数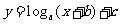 (
(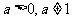 )的图象是由函数
)的图象是由函数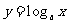 的图象当
的图象当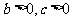 时先向左平移 b个单位,再向上平移c 个单位得到; 当
时先向左平移 b个单位,再向上平移c 个单位得到; 当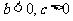 时先向右平移| b|个单位,再向上平移c 个单位得到; 当
时先向右平移| b|个单位,再向上平移c 个单位得到; 当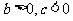 时先向左平移 b个单位,再向下平移|c |个单位得到; 当
时先向左平移 b个单位,再向下平移|c |个单位得到; 当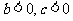 时先向右平移| b|个 单位,再向下平移|c| 个单位得到。
时先向右平移| b|个 单位,再向下平移|c| 个单位得到。
2. 函数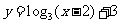 的图象是由函数
的图象是由函数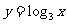 的图象
得到。
的图象
得到。
1.函数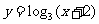 的图象是由函数
的图象是由函数
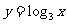 的图象
的图象
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com