
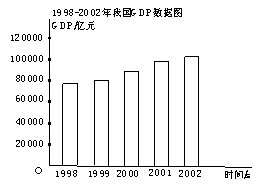
例3:如图,2000年我国国内生产总值(GDP)为89442亿元.如果我国GDP年均增长7.8%左右,按照这个增长速度,在2000年的基础上,经过多少年以后,我国GDP才能实现比2000年翻两番的目标?
[解]
设经过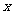 年后我国的GDP实现比2000年翻两番. 则:
年后我国的GDP实现比2000年翻两番. 则:
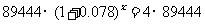
∴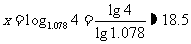
答:约经过19年以后,我国GDP才能实现比2000年番两番.
例4: 要测定古物的年代,可以用放射性碳法:在动植物的体内都含有微量的放射性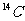 .动植物死亡后,停止了新陈代谢,
.动植物死亡后,停止了新陈代谢,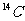 不再产生,且原有的
不再产生,且原有的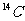 会自动衰变.经过5730年(
会自动衰变.经过5730年(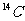 的半衰期),它的残余量只有原始量的一半.我国辽东半岛普兰店附近的泥炭中发掘出的古莲子中
的半衰期),它的残余量只有原始量的一半.我国辽东半岛普兰店附近的泥炭中发掘出的古莲子中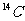 的残余量占原来的87.9%,试推算古莲子的生活年代.
的残余量占原来的87.9%,试推算古莲子的生活年代.
分析:
[解]设经过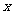 年后的残余量是
年后的残余量是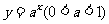 ,由
,由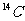 的半衰期是5730年,即
的半衰期是5730年,即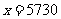 时,
时,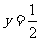 得
得 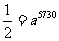 ,
,
∴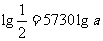 ,
,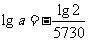 ,∴由
,∴由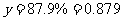 ,知
,知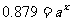
∴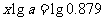 ,∴
,∴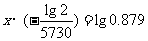
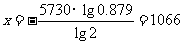
∴古莲子约是1066年前的遗物。
思维点拔:
有关增长率问题,满足关系式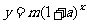 ,其中
,其中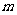 是增长(降低)前的量,
是增长(降低)前的量,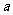 为增长率(降低率),
为增长率(降低率),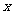 为增长(降低)次数,
为增长(降低)次数,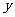 是增长(降低)后的量,要求
是增长(降低)后的量,要求 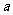 或
或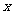 需要对等式两边取对数,选择恰当的底数是关键,在解题过程中,常取常用对数。
需要对等式两边取对数,选择恰当的底数是关键,在解题过程中,常取常用对数。
追踪训练二
1.
2.(法一)由对数定义可知: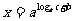
 .
.
(法二)由已知移项可得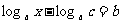 ,
,
即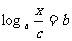 ,由对数定义知:
,由对数定义知: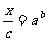 ,
,
∴ 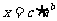 .
.
(法三)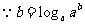 ,
,
∴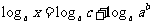
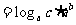 ,
,
∴ 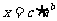 .
.
2.已知: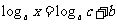 ,求
,求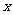
|
学生质疑 |
|
|
教师释疑 |
|
答案:1.∵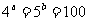
∴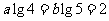 ∴
∴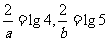
∴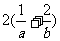
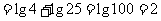
 例5:已知
例5:已知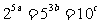 ,求
,求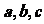 之间的关系。
之间的关系。
分析:由于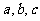 在幂的指数上,所以可考虑用对数式表示出
在幂的指数上,所以可考虑用对数式表示出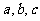 。
。
[解]∵ 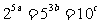 ,∴两边取以10为底的对数得:
,∴两边取以10为底的对数得: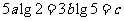
∴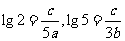 ,∵
,∵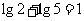
∴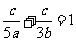
点评:本题要求关于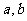 的代数式的值,必须对已知等式两边取对数,恰当的选取对数的底数是十分重要的,同时
的代数式的值,必须对已知等式两边取对数,恰当的选取对数的底数是十分重要的,同时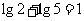 是关键。
是关键。
例6.设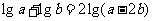 ,
,
求: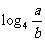 的值
的值
分析:本题只需求出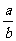 的值,从条件式出发,设法变形为
的值,从条件式出发,设法变形为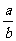 的方程。
的方程。
[解]当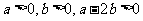 时,原式可化为:
时,原式可化为: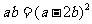 ,即
,即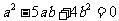
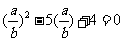 ,∴
,∴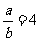 或
或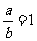 (舍)
(舍)
∴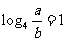
思维点拔:
本题在求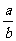 时,不是分别求出
时,不是分别求出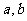 的值,而是把
的值,而是把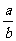 看成一个字母,这种方法称为“整体”思想方法。
看成一个字母,这种方法称为“整体”思想方法。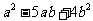 是关于
是关于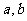 的齐次式,对于齐次式通常都用本题的方法处理。
的齐次式,对于齐次式通常都用本题的方法处理。
对于连比式,通常对等式两边取对数,转化为对数运算,同时化对数的底数相同也是解决对数问题的常用策略.
追踪训练二
1.设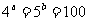 ,求
,求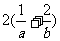 的值。
的值。
例4:计算: ①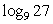 ,②
,② 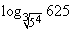 .
.
[解]解:①设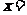
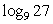 则
则 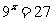 ,
, 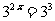 , ∴
, ∴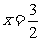 ∴
∴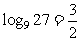
②方法同① 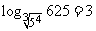
 例5:求 x 的值:
例5:求 x 的值:
①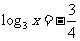 ;
;
②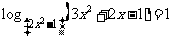 .
.
③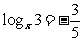
[解]
① 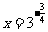
②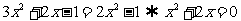
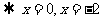 但必须:
但必须: , ∴
, ∴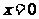 舍去 ,从而
舍去 ,从而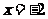 .
.
③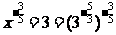 ∴
∴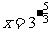 。
。
点评:本题的关键是根据对数的概念,将对数式还原成指数式,但要注意对数式中底数和真数的取值要求。
思维点拔:
要明确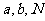 在对数式与指数式中各自的含义,在指数式
在对数式与指数式中各自的含义,在指数式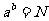 中,
中,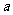 是底数,
是底数,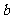 是指数,
是指数,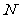 是幂;在对数式
是幂;在对数式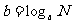 中,
中,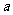 是对数的底数,
是对数的底数,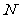 是真数,
是真数,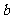 是以
是以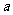 为底
为底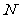 的对数,虽然
的对数,虽然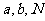 在对数式与指数式中的名称不同,但对数式与指数式有密切的联系:求对数
在对数式与指数式中的名称不同,但对数式与指数式有密切的联系:求对数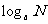 就是求
就是求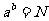 中的指数,也就是确定
中的指数,也就是确定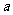 的多少次幂等于
的多少次幂等于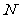 。
。
追踪训练二
求下列各式中的x的值:
⑴logx9=2;⑵lgx2= -2;
⑶log2[log2(log2x)]=0
答案:(1)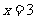 (2)
(2)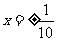
(3)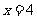
|
学生质疑 |
|
|
教师释疑 |
|
3.已知函数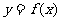 的定义域为[-2,3],则函数
的定义域为[-2,3],则函数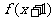 的定义域为[-3,2].
的定义域为[-3,2].
|
学生质疑 |
|
|
教师释疑 |
|
2.函数 的定义域为
的定义域为
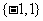 ;
;
例5.求函数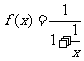 的定义域。
的定义域。
[解]由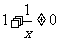 ,得
,得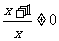 ,∴
,∴ 且
且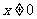 ,即函数的定义域为
,即函数的定义域为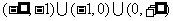 。
。
思维点拨
求函数定义域,不能先化简函数表达式,否则容易出错。如例5,若先化简得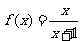 ,此时求得的定义域为
,此时求得的定义域为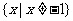 显然是错误的.
显然是错误的.
追踪训练二
1.若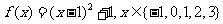 ,则
,则
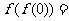 2
;
2
;
例4: 已知函数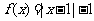 的定义域为
的定义域为
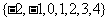 ,求
,求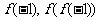 的值.
的值.
分析:求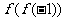 的值,即当
的值,即当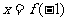 时,求
时,求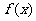 的值。
的值。
[解] ;
;
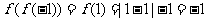
3. 函数f(x)=x-1(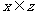 且
且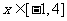 )的值域为
)的值域为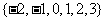 .
.
[选修延伸]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com