
2、求函数y=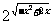 的单调区间.
的单调区间.
答案:利用复合函数单调性的规律,容易得到函数y=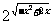 的单调增区间是[0,1],单调减区间是[1,2]。
的单调增区间是[0,1],单调减区间是[1,2]。
例4、已知f(x)=(ex-a)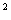 + (e-x-a)
+ (e-x-a)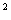 (a
(a 0)。
0)。
(1) f(x)将表示成u= 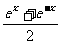 的函数;
的函数;
(2) 求f(x)的最小值
思维分析:平方展开重新配方,就可以得到所求函数的形式;然后根据二次函数的知识确定最值。
[解]:
(1)将f(x) 展开重新配方得,f(x)
=(ex+e-x)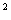 -2a(ex+e-x)+2a
-2a(ex+e-x)+2a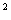 -2
-2
令u= 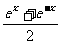 ,得f(x)=4u
,得f(x)=4u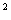 -4au+2 a
-4au+2 a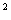 -2(u
-2(u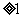 )
)
(2)因为f(u)的对称轴是u=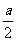 ,又a
,又a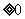
所以当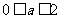 时,则当u=1时,f(u)有最小值,此时f(u)
时,则当u=1时,f(u)有最小值,此时f(u)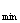 =f(1)=2(a-1)
=f(1)=2(a-1)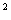 。
。
当a>2时,则当u=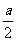 时,f(u)有最小值,此时f(u)
时,f(u)有最小值,此时f(u)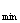 =f (
=f (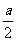 )=a
)=a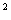 -2.
-2.
所以f(x)的最小值为
f(x)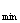 =
=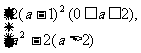
点评:这是复合函数求最值问题,为了求得最值,通过换元转化为二次函数,再由二次函数在区间上的单调性确定最值。
追踪训练
1、求下列函数定义域和值域.
(1)y=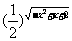 ;
;
(2)y=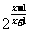
答案:(1)定义域[-1,2];
[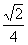 ,1]。
,1]。
(2)定义域{x│x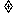 -1}
-1}
值域{y│y>2,或0<y<2}
例3、已知函数f(x)=ax(a>0,且a≠1),根据图象判断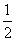 [f(x1)+f(x2)]与f(
[f(x1)+f(x2)]与f(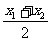 )的大小,并加以证明。
)的大小,并加以证明。
[解]:
由a>1及0<a<1两种情形的指数函数图象可以判断f(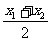 )〈
)〈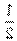 [f(x1)+f(x2)]。
[f(x1)+f(x2)]。
证明如下:f(x1)+f(x2)-2 f(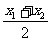 )=
)=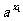 +
+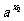 -2a
-2a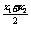 =( a
=( a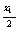 -a
-a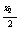 )
)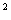 ,由于
,由于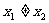 ,所以a
,所以a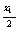 -a
-a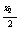
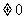 .
.
所以( a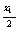 -a
-a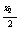 )
)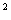 〉0.
〉0.
所以f(x1)+f(x2)-2 f(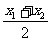 )>0
)>0
即
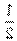 [f(x1)+f(x2)]> f(
[f(x1)+f(x2)]> f(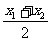 )。
)。
例2、求函数y=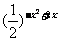 的单调区间。
的单调区间。
[解]:
定义域是R。令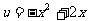 ,则
,则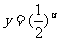 。当
。当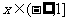 时函数
时函数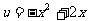 为增函数,
为增函数,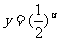 是减函数,所以函数y=
是减函数,所以函数y=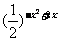 在
在 上是减函数;当
上是减函数;当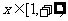 时函数
时函数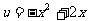 为减函数,
为减函数,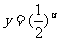 是减函数,所以函数y=
是减函数,所以函数y=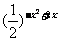 在上
在上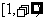 是增函数。
是增函数。
综上,函数y=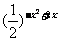 的单调增区间是
的单调增区间是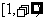 ,单调减区间是
,单调减区间是 。
。
点评:y=a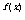 的单调性由a
的单调性由a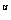 和u=f(x)两函数在相应区间上单调性确定的,遵循“同增异减”法则。
和u=f(x)两函数在相应区间上单调性确定的,遵循“同增异减”法则。
例1、求下列函数的定义域与值域。
(1)y=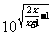 ;
;
(2)y= ;
;
(3)y=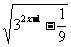
思维分析:y=a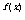 的定义域是f(x)的定义域;对于值域,要先求出f(x)
值域再利用指数函数单调性求解。
的定义域是f(x)的定义域;对于值域,要先求出f(x)
值域再利用指数函数单调性求解。
[解]:
(1)令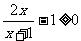 ,得
,得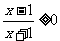 。解得x
。解得x 1,或x<-1。故定义域为
1,或x<-1。故定义域为
{x│x 1,或x<-1}。由于
1,或x<-1}。由于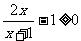 ,且
,且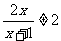 ,所以
,所以
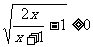 ,
, 
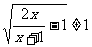
故函数y=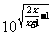 的值域为{y│y
的值域为{y│y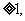 且y
且y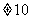 };
};
(2) 定义域为R;由于2x-x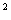 =-(x-1)
=-(x-1)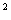 +1
+1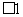 ,所以值域为[
,所以值域为[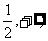 。
。
(3)令3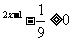 ,所以x
,所以x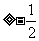 .
.
所以定义域为[-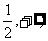 ,值域为[
,值域为[ 。
。
例4: 某工厂今年1月、2月、3月生产某种产品的数量分别是1万件、 万件、
万件、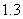 万件,为了估测以后每个月的产量,以这三个月的产品数量为依据.用一个函数模拟该产品的月产量
万件,为了估测以后每个月的产量,以这三个月的产品数量为依据.用一个函数模拟该产品的月产量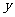 与月份的关系,模拟函数可以选用二次函数或
与月份的关系,模拟函数可以选用二次函数或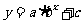 (其中
(其中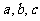 为常数).已知4月份该产品的产量为
为常数).已知4月份该产品的产量为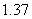 万件,请问用哪个函数作为模拟函数较好并说明理由.
万件,请问用哪个函数作为模拟函数较好并说明理由.
[解]
(1)若选用二次函数,则可设为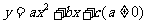
由条件可得:
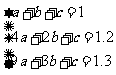 解得:
解得:
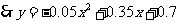
当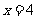 时,
时,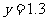 (万件)
(万件)
(2)若选用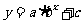
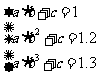 解得
解得
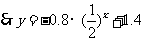
当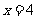 时,
时,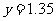 (万件)
(万件)
由(1)(2)可得选用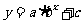 较好.
较好.

追踪训练二
1.某人承包了一片荒山,承包期限为10年,准备栽种5年可成材的树木。该树木从树苗到成材期间每年的木材增长率为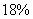 ,以后每年的木材增长率为
,以后每年的木材增长率为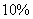 ,树木成材后,既可出售树木,重栽新树苗,也可让其继续生长至承包期满。问:哪一种方案可获得较多的成材木材量?(参考数据:
,树木成材后,既可出售树木,重栽新树苗,也可让其继续生长至承包期满。问:哪一种方案可获得较多的成材木材量?(参考数据: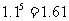 ).
).
解:设新树苗的木材量为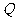 ,
,
①若连续生长10年,木材量为
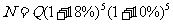 ,
,
②生长5年重栽新树苗,木材量为
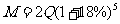 ,
,
则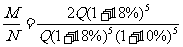
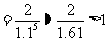 .
.
∴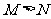 ,
,
生长5年重栽新树苗可获得较大的木材量.
|
学生质疑 |
|
|
教师释疑 |
|
例4: (1)求方程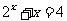 的近似解(精确到
的近似解(精确到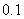 );(2)求不等式
);(2)求不等式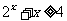 的解集.
的解集.
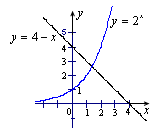 [解]方程
[解]方程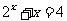 可化为
可化为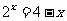 ,
,
分别画出函数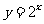 与函数
与函数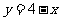 的图象(1)由图象可以知道,方程
的图象(1)由图象可以知道,方程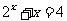 的近似解为
的近似解为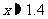 ;(2)不等式
;(2)不等式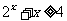 的解集为
的解集为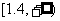 .
.
点评:与指数函数有关的方程与不等式当用代数方法比较困难时,通常将它们拆成两个函数,通过观察函数的图象来求出结果.
追踪训练二
1. 已知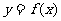 是定义在
是定义在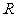 上的奇函数,且
上的奇函数,且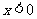 时,
时,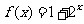 .
.
(1)
求函数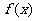 的解析式;(2)画出函数
的解析式;(2)画出函数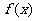 的图象;(3)写出函数
的图象;(3)写出函数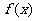 单调区间及值域;(4)求使
单调区间及值域;(4)求使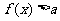 恒成立的实数
恒成立的实数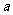 的取值范围.
的取值范围.
解:(1)∵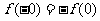 ,∴
,∴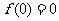 ,
,
又当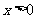 时,
时,
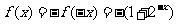 ,
,
∴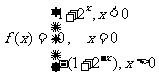 .
.
(2)
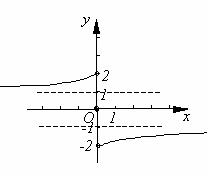 函数
函数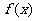 的图象为
的图象为
(3) 根据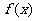 的图象知:
的图象知: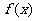 的单调增区间为
的单调增区间为 ,
, ;
;
值域为
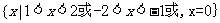 .
.
(4)根据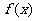 的图象知:使
的图象知:使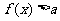 恒成立的实数
恒成立的实数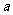 的取值范围为
的取值范围为 .
.
|
学生质疑 |
|
|
教师释疑 |
|
例4: 求函数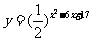 的定义域、值域、单调区间.
的定义域、值域、单调区间.
分析:原函数由函数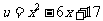 与
与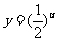 复合而成,求解时要统筹考虑.
复合而成,求解时要统筹考虑.
[解]设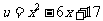 ,则
,则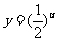 ,由于它们的定义域都是
,由于它们的定义域都是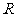 ,所以函数
,所以函数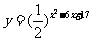 的定义域为
的定义域为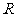 .
.
因为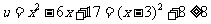 ,
,
所以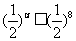 ,又
,又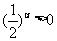 ,
,
函数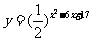 的值域为
的值域为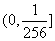 .
.
函数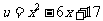 在
在 是增函数,而
是增函数,而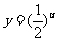 在
在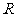 上是减函数,
上是减函数,
所以设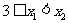 ,则
,则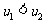 ,
,
从而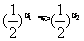 ,即
,即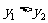 ,
,
函数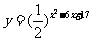 在
在 是增函数,
是增函数,
同理:函数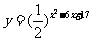 在
在 是减函数,函数
是减函数,函数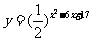 的增区间
的增区间 ,
,
减区间是 .
.
点评:形如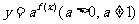 的定义域与
的定义域与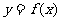 的定义域相同;求值域时要先确定
的定义域相同;求值域时要先确定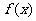 的值域,再根据指数函数的性质确定
的值域,再根据指数函数的性质确定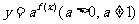 的值域;
的值域;
当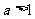 时,
时,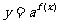 与
与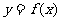 的单调性相同,
的单调性相同,
当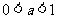 时,
时,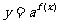 与
与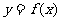 的单调性相反.
的单调性相反.
思维点拔:
(1)比较两个指数式的大小或解指数不等式往往要利用指数函数的性质;(2)与指数函数有关的复合函数的性质既要考虑到指数函数的性质,又要考虑到与之复合的函数性质.
追踪训练二
1.求下列函数的定义域、值域:
(1)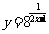 (2)
(2)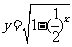
解:(1) ∴
∴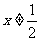
原函数的定义域是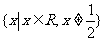 ,
,
令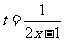 则
则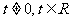
∴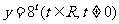 得
得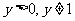 ,
,
所以,原函数的值域是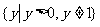 .
.
(2)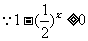 ∴
∴
原函数的定义域是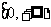 ,
,
令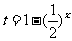
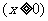 则
则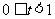 ,
,
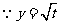 在
在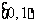 是增函数 ∴
是增函数 ∴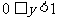 ,
,
所以,原函数的值域是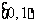 .
.
|
学生质疑 |
|
|
教师释疑 |
|
3.设a>1,b>0,ab+a-b=2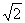 ,则ab-a-b()
,则ab-a-b()
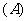
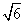
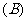
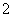 或
或
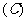

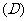
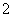
|
学生质疑 |
|
|
教师释疑 |
|
2.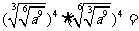 (
(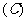 )
)
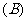
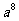
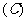
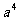
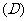
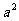
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com