
3.万能公式的推导
1°
2°
3°
[精典范例]
例1已知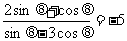 ,求3cos 2q + 4sin 2q 的值.
,求3cos 2q + 4sin 2q 的值.
例2已知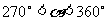 ,化简
,化简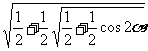 .
.
例3已知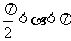 ,
,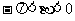 ,tana =
,tana =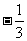 ,tanb =
,tanb =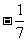 ,求2a + b .
,求2a + b .
 例4已知sina - cosa =
例4已知sina - cosa = 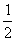 ,
,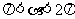 ,求
,求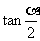 和tana的值.
和tana的值.
例5已知cosa - cos b = 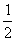 ,sina - sinb =
,sina - sinb = 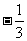 ,求sin(a + b)的值.
,求sin(a + b)的值.
例6已知A、B、C是三角形的内角,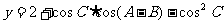 .
.
(1)问任意交换两个角的位置,y的值是否变化?试证明你的结论。
(2)求y 的最大值。
思维点拔:
2.和差化积公式的推导
在上式中若令a + b = q,a - b = φ,则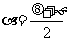 ,
,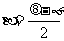 代入得:
代入得:
∴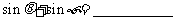
1.积化和差公式的推导
因为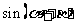 和
和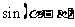 是我们所学习过的知识,因此我们考虑
是我们所学习过的知识,因此我们考虑
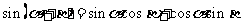 ;
;
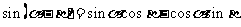 .
.
两式相加得
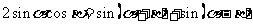 即
即 ;
;
2.注意半角公式的推导与正确使用.
学习重点
几组三角恒等式的应用
学习难点
灵活应用和、差、倍角等公式进行三角式化简、求值、证明恒等式
[自学评价]
1.掌握推导积化和差、和差化积公式、半角公式和万能公式的方法,知道它们的互化关系
6.万能公式
 7.派生公式:
7.派生公式:
(1) (sinα±cosα)2=1±sin2α.
(2)
1+cosα=2cos2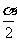 ,
,
(3
)1-cosα=2sin2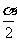 ,
,
(4) asinα+bcosα
=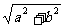 sin(α+φ)
sin(α+φ)
= cos(α-
cos(α-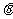 )
)
(5)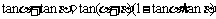
学习要求
5.和差化积公式

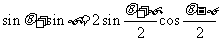
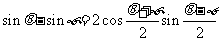

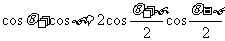

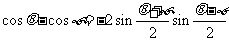

4.积化和差公式
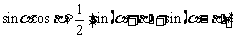
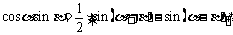
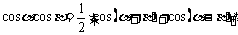
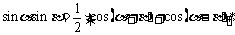
3.半角公式
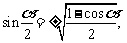
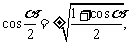
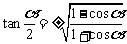
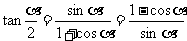
2.倍角降幂公式
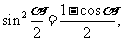
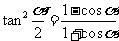
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com