
3.计算:cos65°cos115°-cos25°sin115°
解:原式= cos65°cos115°-sin65°sin115°=cos(65°+115°)=cos180°=-1
4 计算:-cos70°cos20°+sin110°sin20°
计算:-cos70°cos20°+sin110°sin20°
原式=-cos70°cos20°+sin70°sin20°=-cos(70°+20°)=0
2.求cos75°的值
解:cos75°=cos(45°+30°)=cos45°cos30°-sin45°sin30°
=
1.sina-sinb=-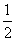 ,cosa-cosb=
,cosa-cosb=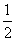 ,aÎ(0,
,aÎ(0, 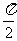 ),bÎ(0,
),bÎ(0, 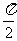 ),求cos(a-b)的值。
),求cos(a-b)的值。
解: ∵sina-sinb=-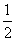 ,cosa-cosb=
,cosa-cosb=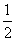 ,aÎ(0,
,aÎ(0, 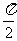 ),bÎ(0,
),bÎ(0, 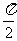 ),
),
∴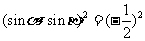 ,
,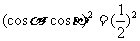
∴2-2 cos(a-b)=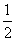 ∴cos(a-b)=
∴cos(a-b)=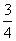
8.探究 cos(a-b)的公式
以-b代b得: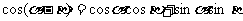
公式记号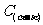
[精典范例]
例1 计算① cos105° ②cos15° ③cos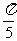 cos
cos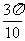 -sin
-sin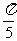 sin
sin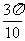
解:①cos105°=cos(60°+45°)=cos60°cos45°-sin60°sin45°
=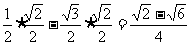
②cos15° =cos(60°-45°)=cos60°cos45°+sin60°sin45°
=
③cos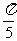 cos
cos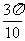 -sin
-sin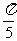 sin
sin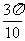 = cos(
= cos(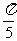 +
+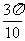 )=cos
)=cos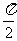 =0
=0
例2已知sina=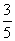 ,cosb=
,cosb=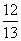 求cos(a-b)的值
求cos(a-b)的值
解:∵sina=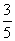 >0,cosb=
>0,cosb=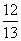 >0
>0
∴a可能在一、二象限,b在一、四象限
若a、b均在第一象限,
则cosa=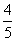 ,sinb=
,sinb=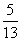 cos(a-b)=
cos(a-b)=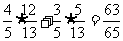
若a在第一象限,b在四象限,
则cosa=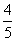 ,sinb=-
,sinb=-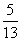 cos(a-b)=
cos(a-b)=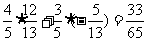
若a在第二象限,b在一象限,
则cosa=-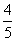 ,sinb=
,sinb=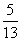 cos(a-b)=
cos(a-b)=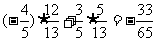
若a在第二象限,b在四象限,
则cosa=-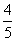 ,sinb=-
,sinb=-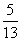 cos(a-b)=
cos(a-b)=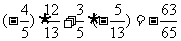
例3已知cos(2α-β)=-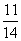 ,sin (α-2β)=
,sin (α-2β)=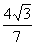 ,且
,且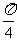 <α<
<α<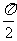 ,0<β<
,0<β<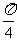 ,
,
求cos(α+β)的值。
分析:已知条件中的角与所求角虽然不同,但它们之间有内在联系,
即(2α-β)-(α-2β)=α+β 由α、β角的取值范围,分别求出2α-β、α-2β角的正弦和余弦值,再利用公式即可求解。
由α、β角的取值范围,分别求出2α-β、α-2β角的正弦和余弦值,再利用公式即可求解。
解:∵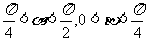 ,
,
∴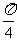 <2α-β<π,-
<2α-β<π,- 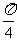 <α-2β<
<α-2β<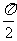 ,
,
由cos(2α-β)=-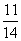 得,sin (2α-β)=
得,sin (2α-β)=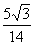 ;
;
由sin
(α-2β)=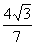 得,cos(α-2β)=
得,cos(α-2β)=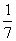 。
。
∴cos(α+β)=cos[(2α-β)-(α-2β)]=cos(2α-β)cos(α-2β)+sin (2α-β)sin (α-2β)=- 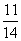 ×
×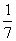 +
+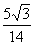 ×
×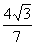 =
=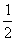 。
。
例4不查表,求下列各式的值.
(1)
(2)
(3)
思维点拔:
在三角变换中,首先应考虑角的变换 如何变换角?一定要根据题目的条件与结论来变,简单地说就是“据果变形”,创造出使用三角公式的条件,以达到求值、化简和证明的目的
如何变换角?一定要根据题目的条件与结论来变,简单地说就是“据果变形”,创造出使用三角公式的条件,以达到求值、化简和证明的目的 常用的变换角的方法有:α=(α+β)-β,α+2β=(α+β)+α,
常用的变换角的方法有:α=(α+β)-β,α+2β=(α+β)+α,
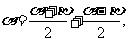
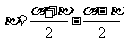 ,…
,…
[追踪训练]:
7.探究 特征
①熟悉公式的结构和特点;
②此公式对任意a、b都适用
③公式记号
6.探究 由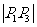 =
=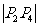 导出公式
导出公式
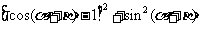

展开并整理得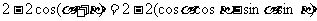
所以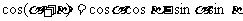 可记为
可记为 
5.计算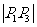 ,
,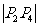
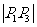 =
=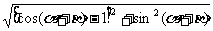
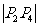 =
=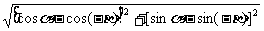
4.探究:写出4个点的坐标
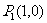 ,
,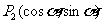
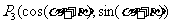 ,
,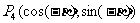 ,
,
3.探究:作单位圆,构造全等三角形
2.探究:在坐标系中a、b角构造a+b角
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com