
3、三角恒等变换具有几何和物理的应用背景。以向量为桥梁将三角恒等变换的算式与直观的几何图形相互沟通和转化,有助于学习和应用三角恒等变换,还能提高学习数学的兴趣,体会数学是一个有机联系的整体,二不是各不相关的内容的堆积。
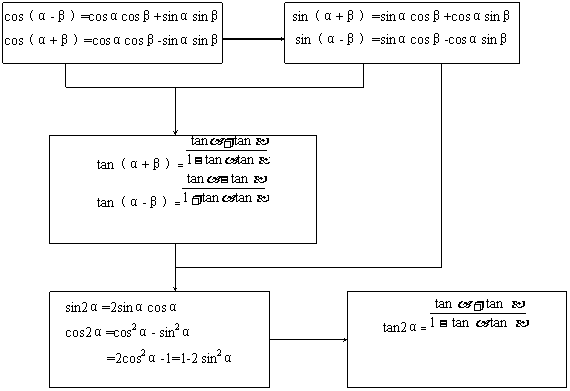 知识网络
知识网络
学习要求
2. 三角恒等变换位于三角函数与数学变换的结合点上。三角恒等变换公式反映了角的相加、相减、二倍角运算引起三角函数值变化的规律,是研究三角函数性质及其应用的一种工具。学习和应用三角恒等变换,有利于发展推理能力和运算能力。
1. 本章利用向量的数量积推导出两角差的余弦公式,并由此公式导出两角和与差的正弦、余弦、正切公式;二倍角的正弦、余弦、正切公式等,以及运用这些公式进行简单的恒等变换。
4.求证:(1)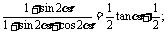
(2)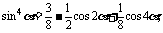
(3)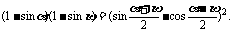
3.求值: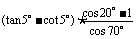 = .
= .
2.已知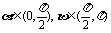 ,且
,且
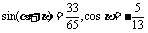 ,则
,则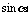 的值等于 ( )
的值等于 ( )
A.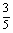 B.
B.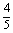 C.
C.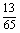 D.
D.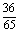
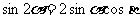 2cos2α=1+cos2α 2sin2α=1-cos2α
2cos2α=1+cos2α 2sin2α=1-cos2α
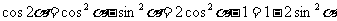
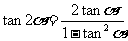
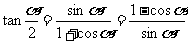

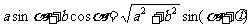
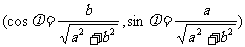
注意:倍角公式揭示了具有倍数关系的两个角的三角函数的运算规律,可实现函数式的降幂的变化。
注: (1)两角和与差的三角函数公式能够解答的三类基本题型:求值题,化简题,证明题。
(2)对公式会“正用”,“逆用”,“变形使用”;
(3)掌握“角的演变”规律,
(4)将公式和其它知识衔接起来使用。
重点难点
重点:几组三角恒等式的应用
难点:灵活应用和、差、倍角等公式进行三角式化简、求值、证明恒等式
[精典范例]
例1 已知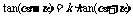
求证: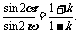
例2 已知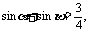 求
求 的取值范围
的取值范围
分析  难以直接用
难以直接用 的式子来表达,因此设
的式子来表达,因此设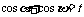 ,并找出
,并找出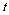 应满足的等式,从而求出
应满足的等式,从而求出 的取值范围.
的取值范围.
例3 求函数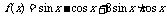 的值域.
的值域.
例4
已知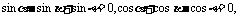
且 、
、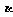 、
、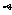 均为钝角,求角
均为钝角,求角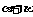 的值.
的值.
分析 仅由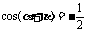 ,不能确定角
,不能确定角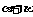 的值,还必须找出角
的值,还必须找出角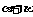 的范围,才能判断
的范围,才能判断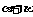 的值. 由单位圆中的余弦线可以看出,若
的值. 由单位圆中的余弦线可以看出,若 使
使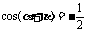 的角为
的角为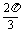 或
或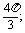 若
若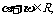 则
则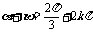 或
或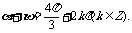
[选修延伸]
例5
已知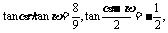
求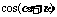 的值.
的值.
例6
已知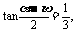 ,
,
求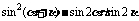 的值.
的值.
例7
已知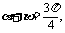
求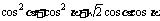 的值.
的值.
例8 求值:(1)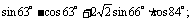 (2)
(2)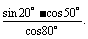
[追踪训练]
1.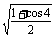 等于 ( )
等于 ( )
A.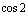 B.
B.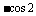 C.
C.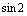 D.
D.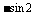
9.求证
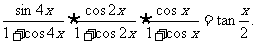
[师生互动]
|
学生质疑 |
|
|
教师释疑 |
|
8.已知cos2θ=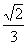 ,求sin4θ+cos4θ的值.
,求sin4θ+cos4θ的值.
7. 设25sin2x+sinx-24=0且x是第二象限角,求tan
设25sin2x+sinx-24=0且x是第二象限角,求tan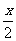 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com