
2.若三条线段的长为5,6,7,则用这三条线段( ) A.能组成直角三角形
B.能组成锐角三角形
C.能组成钝角三角形
D.不能组成三角形
1.在△ABC中,
(1)已知A=60°,b=4,c=7,
求a;
(2)已知a=7,b=5,c=3,求A.
2.利用余弦定理,可以解决以下两类解斜三角形的问题:
(1)_______________________________;
(2)_______________________________.
[精典范例]
[例1]在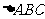 中,
中,
(1)已知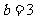 ,
,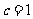 ,
,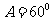 ,求
,求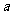 ;
;
(2)已知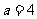 ,
,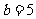 ,
,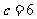 ,求
,求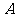 (精确到
(精确到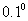 ).
).
[解]
点评: 利用余弦定理,可以解决以下两类解斜三角形的问题:(1)已知三边,求三个角;(2)已知两边和它们的夹角,求第三边和其他两个角.
 [例2]
[例2]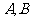 两地之间隔着一个水塘,现选择另一点
两地之间隔着一个水塘,现选择另一点 ,测
,测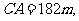
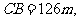
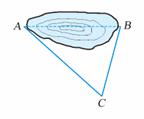
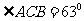 ,求
,求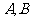 两地之间的距离(精确到
两地之间的距离(精确到 ).
).
[解]
[例3]用余弦定理证明:在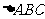 中,当
中,当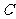 为锐角时,
为锐角时,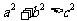 ;当
;当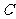 为钝角时,
为钝角时,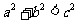 .
.
[证]
点评:余弦定理可以看做是勾股定理的推广.
追踪训练一
1.余弦定理:
(1)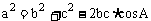 ,______________________,______________________.
,______________________,______________________.
(2) 变形: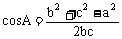 ,___________________,___________________ .
,___________________,___________________ .
3. 能初步运用余弦定理解斜三角形.
[课堂互动]
自学评价
2. 体会向量的工具性;
1. 掌握余弦定理及其证明;
1.2 余弦定理
第1课时
知识网络
三角形中的向量关系→余弦定理
学习要求
6.在△ABC中,
证明: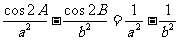 .
.

5.已知△ABC中,sinA∶sinB∶sinC=k∶(1-2k)∶3k(k≠0),则k的取值范围为 ( )
A.(2,+∞) B.(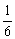 ,
,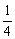 )
)
C.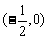 D.
D.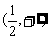
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com