
3.判断△ABC的形状.
[课堂互动]
自学评价
2.熟记正弦定理及其变形形式;
1.掌握正弦定理和三角形面积公式,并能运用这两组公式求解斜三角形;
2.某人站在山顶向下看一列车队向山脚驶来,他看见第一辆车与第二辆车的俯角差等于他看见第二辆车与第三辆车的俯角差,则第一辆车与第二辆车的距离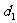 与第二辆车与第三辆车的距离d2之间的关系为 ( C )
与第二辆车与第三辆车的距离d2之间的关系为 ( C )
A.  B.
B.

C.  D.
不能确定大小
D.
不能确定大小

|

1.一船向正北航行,看见正西方向有相距10海里的两个灯塔恰好与它在一条直线上,继续航行半小时后,看见一灯塔在船的南偏西60°, 另一灯塔在船的南偏西75°,则这只船的速度是每小时 ( C )
A.5海里? B.5 海里
海里
C.10海里? D.10 海里
海里
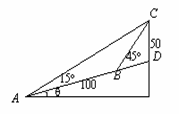
3.如图:在斜度一定的山坡上的一点A测得山顶上一建筑物顶端C对于山坡的斜度为15°,向山顶前进100m后,又从点B测得斜度为45°,假设建筑物高50m,求此山对于地平面的斜度q
[解]在△ABC中,AB = 100m , ÐCAB = 15°, ÐACB = 45°-15° = 30°
由正弦定理: ∴BC = 200sin15°
∴BC = 200sin15°
在△DBC中,CD = 50m , ÐCBD = 45°, ÐCDB = 90° + q
 由正弦定理:
由正弦定理: Þcosq =
Þcosq =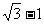 ,
,
∴q = 42 94°
94°
[选修延伸]
[例5]在湖面上高h处,测得云彩仰角为a,而湖中云彩影的俯角为b,求云彩高.
[解]C、C’关于点B对称,设云高CE = x,
则CD = x - h,C’D = x + h,
在Rt△ACD中,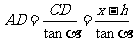
在Rt△AC’D中,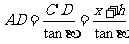 ,
,
∴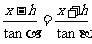
解得 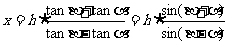 .
.
追踪训练二
2.有一长为1公里的斜坡,它的倾斜角为20°,现要将倾斜角改为10°,则坡底要伸长( A )
A. 1公里 B. sin10°公里
C. cos10°公里 D. cos20°公里
1.海上有A、B两个小岛相距10海里,从A岛望C岛和B岛成60°的视角,从B岛望C岛和A岛成75°的视角,则B、C间的距离是 ( D )
A.10 海里 B.
海里 B.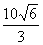 海里
海里
C.
5 海里? D.5
海里? D.5 海里
海里
2.三角形的面积公式:
(1) =
= =
=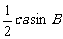
(2)s=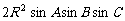
(3)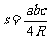
[精典范例]
[例1] 如图,某登山队在山脚A处测得山顶B的仰角为35°,沿倾斜角为20°的斜坡前进1000m后到达D处,又测得山顶的仰角为65°,求山的高度BC(精确到1m).
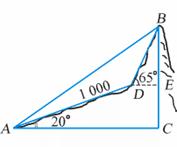 分析:要求BC,只要求AB,为此考虑
分析:要求BC,只要求AB,为此考虑
解△ABD.
[解]
 过点D 作DE ∥AC 交BC 于E,因为 ∠DAC =20°,所以∠ADE=160°,于是∠ADB=360°-160°-65°=135°.又∠BAD=35°-20°=15°,所以∠ABD=30°.
过点D 作DE ∥AC 交BC 于E,因为 ∠DAC =20°,所以∠ADE=160°,于是∠ADB=360°-160°-65°=135°.又∠BAD=35°-20°=15°,所以∠ABD=30°.
在△ABD中,由正弦定理,得 (m).
(m).
在Rt△ABC中,BC=ABsin35°=1000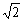 sin35°≈811(m).
sin35°≈811(m).
答 山的高度约为811m.
[例2]在埃及,有许多金字塔形的王陵,经过几千年的风化蚀食,有不少已经损坏了,考古人员在研究中测得一座金字塔的横截面如图(顶部已经坍塌了),∠A=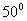 ,∠B=
,∠B=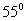 ,AB=120m,如何求得它的高?
,AB=120m,如何求得它的高?
(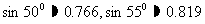 )
)
 分析:本题可以转化成:(1)解三角形,确定顶点C;
分析:本题可以转化成:(1)解三角形,确定顶点C;
(2)求三角形的高。
[解]
(1)先分别沿A、B延长断边,确定交点C,∠C=1800-∠A-∠B,用正弦定理算出AC或BC;
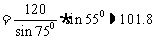
(2)设高为h,则

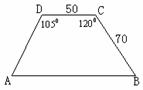 [例3]一座拦水坝的横断面为梯形,如图所示,求拦水坝的横断面面积。(请用计算器解答,精确到
[例3]一座拦水坝的横断面为梯形,如图所示,求拦水坝的横断面面积。(请用计算器解答,精确到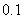 )
)
[解]
连接BD,设∠BDC= ,则由正弦定理知
,则由正弦定理知
 ,即
,即

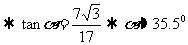 ,从而有
,从而有
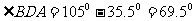 ,
,
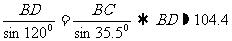 ,由
,由
于 ,即
,即
 ,
,
而梯形的高
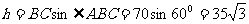
所以有

注:本题也可以构造直角三角形来解,过C作CE⊥AB于E,过D作DF⊥AB于F即可。
[例4]已知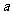 、
、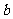 、
、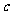 是△ABC中∠A、
是△ABC中∠A、
∠B、∠C的对边, 是△ABC的面积,若
是△ABC的面积,若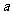 =4,
=4,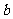 =5,
=5, =
= ,求
,求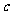 的长度。
的长度。
[解]
由三角形的面积公式得: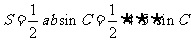
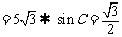
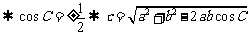
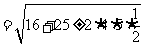 ,
,
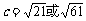
 追踪训练一
追踪训练一
1.正弦定理:在△ABC中,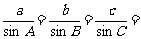
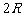 ,
,
变形:(1)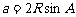 ,
, ,
,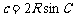
(2) ,
,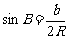 ,
,
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com