
19.方法一:
(1)证明:连结AC,AC交BD于O,连结EO
∵底面ABCD是正方形,∴点O是AC的中点
在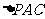 中,EO是中位线,∴PA // EO
中,EO是中位线,∴PA // EO
而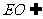 平面EDB且
平面EDB且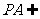 平面EDB,
平面EDB,
所以,PA // 平面EDB. ................4分
(2)证明:∵PD⊥底面ABCD且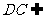 底面ABCD,∴
底面ABCD,∴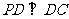
∵PD=DC,可知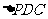 是等腰直角三角形,而DE是斜边PC的中线,
是等腰直角三角形,而DE是斜边PC的中线,
 ∴
∴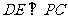
 ①
①
同样由PD⊥底面ABCD,得PD⊥BC
∵底面ABCD是正方形,有DC⊥BC,∴BC⊥平面PDC
而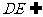 平面PDC,∴
平面PDC,∴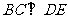
 ②
②
由①和②推得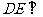 平面PBC
平面PBC
而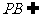 平面PBC,∴
平面PBC,∴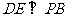
又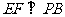 且
且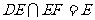 ,所以PB⊥平面EFD
,所以PB⊥平面EFD
.................8分
(3)设正方形边长为1,
由PD⊥平面ABCD,∴ PD⊥BC,
又∵ BC⊥CD,PD∩CD=D,∴BC⊥平面PCD,
∴ BC⊥PC.
在△BDE中,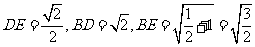 ,
,
∴ 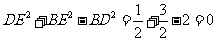 ,即DE⊥BE.
,即DE⊥BE.
而由(2),PB⊥平面EFD,有PB⊥DE,因而DE⊥平面BEF,
∴DE⊥EF,则∠BEF即为二面角B-DE-F的平面角.
Rt△BEF中,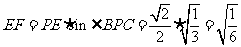 ,
,
∴ 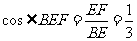 ,即二面角B-DE-F的余弦值为
,即二面角B-DE-F的余弦值为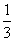 . ........14分
. ........14分
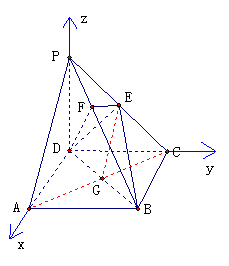
方法二:如图所示建立空间直角坐标系,D为坐标原点,设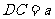

(1)证明:连结AC,AC交BD于G,连结EG
依题意得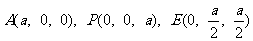

∵底面ABCD是正方形,∴G是此正方形的中心,故点G的坐标为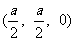 且
且
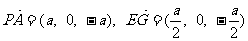

∴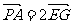 ,这表明PA//EG
,这表明PA//EG
而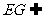 平面EDB且
平面EDB且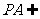 平面EDB,∴PA//平面EDB
平面EDB,∴PA//平面EDB
 ...........4分
...........4分
(2)证明;依题意得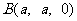 ,
,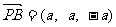
 又
又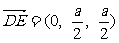 ,故
,故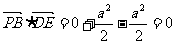

∴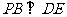

由已知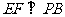 ,且
,且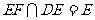 ,所以
,所以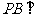 平面EFD
平面EFD ...............8分
...............8分
(3)由(2),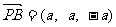 是平面EFD的法向量,
是平面EFD的法向量,
设平面BDE的法向量为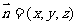 ,= (a, a, 0),
,= (a, a, 0),
由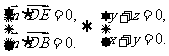
取z = -1,则 ,
,
∴ 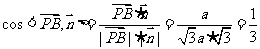 .
.
即二面角B-DE-F的余弦值为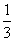 . ............14分
. ............14分
18.解:(1)由已知,点M到直线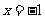 的距离等于到点(1,0)的距离,所以点M是以F(1, 0)为焦点,以
的距离等于到点(1,0)的距离,所以点M是以F(1, 0)为焦点,以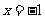 为准线的抛物线,焦点到准线的距离p = 2, ........2分
为准线的抛物线,焦点到准线的距离p = 2, ........2分
∴ 点M的轨迹方程为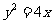 .
.........4分
.
.........4分
(2)设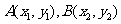 ,由
,由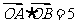 可得:
可得: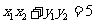 ①
①
∵ A、B均在抛物线上,
∴ 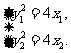 Þ
Þ 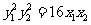 ②
②
由①②可得: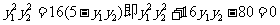 ,
,
∴ 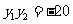 或
或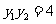 (舍去).
.............8分
(舍去).
.............8分
再由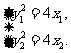 相减得:
相减得: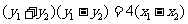 ,
,
若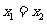 ,则AB⊥x轴,
,则AB⊥x轴,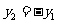 ,由①:
,由①: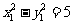 ,结合
,结合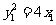 得:
得: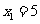 ,
,
∴ 此时AB的方程为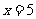 .
..............9分
.
..............9分
若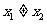 ,则
,则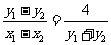 ,即为直线AB的斜率,而
,即为直线AB的斜率,而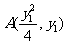 ,则AB的方程为:
,则AB的方程为:
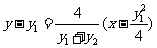 ,
.............11分
,
.............11分
即 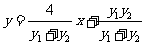 ,
,
∴ 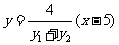 也过定点 (5, 0).
...............13分
也过定点 (5, 0).
...............13分
综上得:直线AB过定点 (5, 0). ...............14分
17.解:(Ⅰ)设A、B、C分别为甲、乙、丙三台机床各自加工的零件是一等品的事件.
|
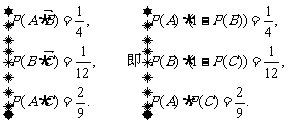 .......2分
.......2分
由①、③得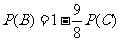 代入②得 27[P(C)]2-51P(C)+22=0.
代入②得 27[P(C)]2-51P(C)+22=0.
解得 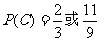 (舍去).
................4分
(舍去).
................4分
将 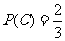 分别代入 ③、② 可得
分别代入 ③、② 可得 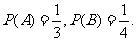
即甲、乙、丙三台机床各加工的零件是一等品的概率分别是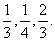 ......6分
......6分
(Ⅱ)x = 0, 1, 2, 3. ......................7分
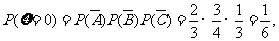 ......................8分
......................8分
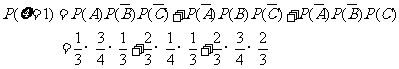
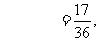 .....................9分
.....................9分
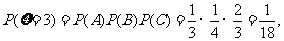 .....................10分
.....................10分
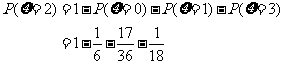
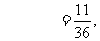 ......................11分
......................11分
∴ 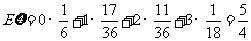 . ......................12分
. ......................12分
解二:设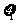 为甲加工的一等品零件数,
为甲加工的一等品零件数,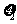 为乙加工的一等品零件数,
为乙加工的一等品零件数,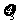 为丙加工的一等品零件数,则x =
为丙加工的一等品零件数,则x = 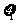 +
+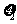 +
+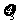 ,
,
∴ 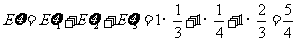 . ......................12分
. ......................12分
16.解:∵ 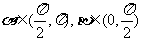 ,
,
∴ 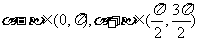 ,
.................2分
,
.................2分
∴ 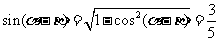 ,
................5分
,
................5分
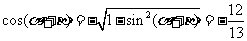 ,
................8分
,
................8分
∴ 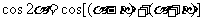
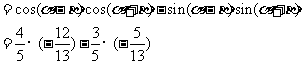
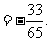 .................12分
.................12分
(二)选做题(13-15题,考生只能从中选做两题)
13. .解析:因为
.解析:因为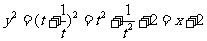 ,而
,而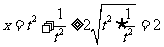 .
.
14.2.解析:由柯西不等式,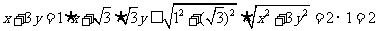 ,
,
当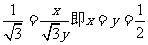 时取得最大值2.
时取得最大值2.
15.90°.解析:因为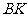 是圆
是圆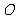 的切线,
的切线,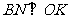 .有
.有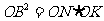 ,又
,又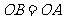 ,
,
所以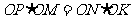 ,即
,即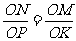 .又
.又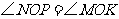 ,
,
所以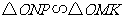 ,故
,故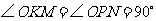 .
.
(一)必做题(9-12题)
9.2.解析:当x=-1时,即输出,此时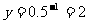 .
.
10.-18.解析: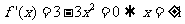 ,
,
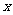 |
-3 |
(-3,-1) |
-1 |
(-1,1) |
1 |
(1,3) |
3 |
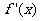 |
|
- |
0 |
+ |
0 |
- |
|
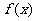 |
18 |
↘ |
-2 |
↗ |
2 |
↘ |
-18 |
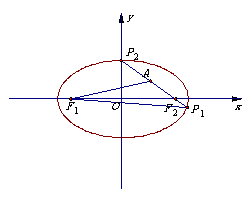 故最小值为-18.
故最小值为-18.
11.4.解析: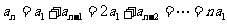 ,故
,故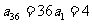 .
.
12.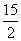 .解析:如图,由于
.解析:如图,由于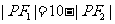 ,因而
,因而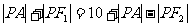 ,又因为
,又因为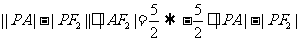
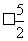 ,当点P在图中P2处时,
,当点P在图中P2处时, =
=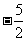 ,所以
,所以 的最大值为10-
的最大值为10-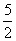 =
=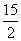 .
.
8.D.解析:首先易知-T、0、T是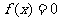 的根,若在(0, T)上没有根,则恒有
的根,若在(0, T)上没有根,则恒有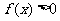 或
或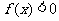 ;不妨设
;不妨设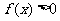 ,则
,则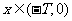 时,
时,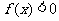 ,但又有
,但又有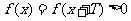 ,矛盾.故
,矛盾.故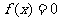 在(0, T)上至少还有一个根.同理,在(-T,0)上也至少还有一个根,故至少有5个根.
在(0, T)上至少还有一个根.同理,在(-T,0)上也至少还有一个根,故至少有5个根.
7.C.解析:由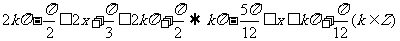 ,取k=0与
,取k=0与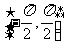 取交集即得.
取交集即得.
6.A.解析:由图易知,选A.
5.D.解析:如图,满足题设的x,y范围如阴影区域所示,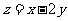 即为
即为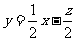 ,在边界点
,在边界点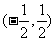 处直线的截距
处直线的截距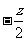 取得最大值 ,所以
取得最大值 ,所以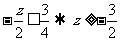 ,得z的最小值为
,得z的最小值为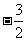 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com