
2.判断该三角形的形状一般都有角化边或边化角两种思路.
[精典范例]
[例1]在 ABC中,求证:
ABC中,求证:
(1)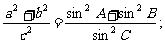
(2)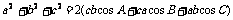
分析:
[解]
(1)根据正弦定理,可设
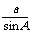 =
= 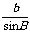 =
= 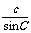 = k
= k
显然 k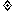 0,所以
0,所以
左边=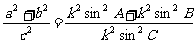
=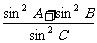 =右边
=右边
(2)根据余弦定理的推论,
右边=2(bc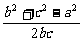 +ca
+ca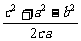 +ab
+ab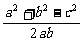 ) =(b
) =(b +c
+c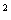 - a
- a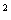 )+(c
)+(c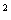 +a
+a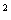 -b
-b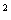 )+(a
)+(a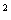 +b
+b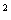 -c
-c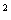 )
)
=a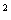 +b
+b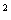 +c
+c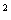 =左边
=左边
[例2]在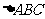 中,已知acosA = bcosB用两种方法判断该三角形的形状.
中,已知acosA = bcosB用两种方法判断该三角形的形状.
 分析:利用正弦定理或余弦定理,“化边为角”或“化角为边”。
分析:利用正弦定理或余弦定理,“化边为角”或“化角为边”。
[解]方法1o(余弦定理)得
a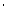
 =b
=b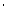

 c
c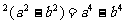 =
=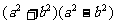

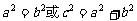

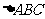 是等腰三角形或直角三角形.
是等腰三角形或直角三角形.
方法2o(正弦定理)得
sinAcosA=sinBcosB,
 sin2A=sin2B,
sin2A=sin2B,
 2A=2B,或2A+2B=180
2A=2B,或2A+2B=180
 A=B或A+B=90
A=B或A+B=90

 是等腰三角形或直角三角形.
是等腰三角形或直角三角形.
点评: 判断该三角形的形状一般都有“走边”或“走角”两条路。
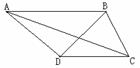 [例3]在四边形ABCD中,
[例3]在四边形ABCD中, ADB=
ADB= BCD=75
BCD=75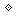 ,
,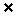 ACB=
ACB=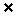 BDC=45
BDC=45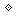 ,DC=
,DC=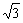 ,求:
,求:
(1) AB的长
(2) 四边形ABCD的面积
[解](1)因为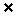 BCD=75
BCD=75 ,
, ACB=45
ACB=45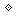 ,
,
所以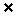 ACD=30
ACD=30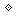 ,又因为
,又因为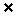 BDC=45
BDC=45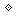 ,
,
所以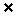 DAC=180
DAC=180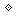 -(75
-(75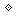 + 45
+ 45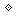 + 30
+ 30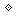 )=30
)=30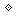 ,
,
所以, AD=DC=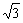
在 BCD中,
BCD中,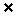 CBD=180
CBD=180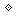 -(75
-(75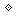 + 45
+ 45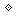 )=60
)=60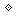 ,所以
,所以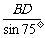 =
= 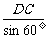 ,
,
BD = 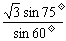 =
= 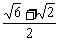
在 ABD中,AB
ABD中,AB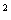 =AD
=AD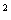 + BD
+ BD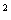 -2
-2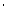 AD
AD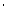 BD
BD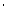 cos75
cos75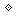 = 5,
= 5,
所以,
AB=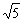
(3)
S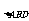 =
=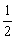
 AD
AD BD
BD sin75
sin75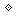
=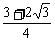
同理, S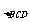 =
= 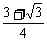
所以四边形ABCD的面积S=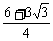
追踪训练一
1.余弦定理:
(1)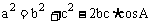 ,
,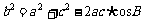 ,
,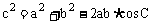 .
.
(2) 变形: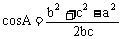 ,
,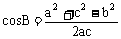 ,
,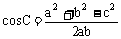
3.进一步运用余弦定理解斜三角形.
[课堂互动]
自学评价
2.能够利用正、余弦定理判断三角形的形状;
1.余弦定理的教学要达到“记熟公式”和“运算正确”这两个目标;
3. 用余弦定理证明:在△ABC中,
用余弦定理证明:在△ABC中,
(1)a=bcosC+ccosB;
(2)b=ccosA+acosC;
(3)c=acosB+bcosA.
|

2.在△ABC中,设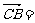
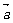 ,
,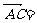
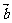 ,且|
,且|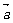 |=2,|
|=2,|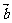 |=
|=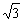 ,
,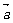 ·
·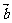 =-
=-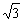 ,求AB的长.
,求AB的长.
略解: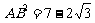
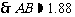
1.在△ABC中,A=60°,b=1,其面积为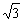 ,则
,则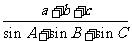 等于( B )
等于( B )
A.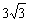 B.
B.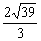 C.
C.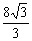 D.
D.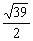
3. 在△ABC中,已知a=2,b=3,C=60°,试证明此三角形为锐角三角形.
[选修延伸]
 [例4]在△ABC中,设
[例4]在△ABC中,设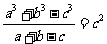 ,且
,且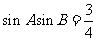 ,请判断三角形的形状。
,请判断三角形的形状。
[解]由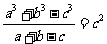 ,
,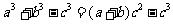 即
即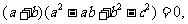 而
而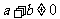 ,得
,得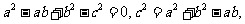
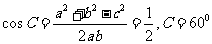
而由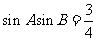 得
得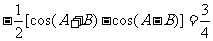
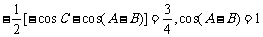 而
而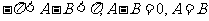 ,
,
∴三角形为等边三角形。
追踪训练二
2.如图,长7m的梯子BC靠在斜壁上,梯脚与壁基相距1.5m,梯顶在沿着壁向上6m的地方,求壁面和地面所成的角α(精确到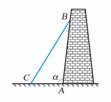 0.1°).
0.1°).
略解:
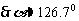
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com