
2. 在运用正弦定理、余弦定理解决实际问题时,通常都根据题意,从实际问题中抽象出一个或几个三角形,然后通过这些三角形,得出实际问题的解。
[课堂互动]
自学评价
运用正弦定理、余弦定理解决实际问题的基本步骤是:
①分析:理解题意,弄清清与未知,画出示意图(一个或几个三角形);
②建模:根据书籍条件与求解目标,把书籍量与待求量尽可能地集中在有关三角形中,建立一个解斜三角形的数学模型;
③求解:利用正弦定理、余弦定理理解这些三角形,求得数学模型的解;
④检验:检验上述所求的解是否符合实际意义,从而得出实际问题的解。
[精典范例]
[例1]作用在同一点的三个力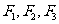 平衡.已知
平衡.已知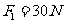 ,
,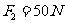 ,
,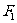 与
与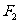 之间的夹角是
之间的夹角是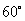 ,求
,求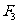 的大小与方向(精确到
的大小与方向(精确到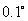 ).
).
[解]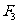 应和
应和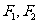 合力
合力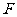 平衡,所以
平衡,所以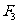 和
和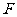 在同一直线上,
在同一直线上,
并且大小相等,方向相反.
如图1-3-3,在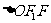 中,由余弦定理,得
中,由余弦定理,得
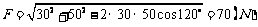 再由正弦定理,得
再由正弦定理,得
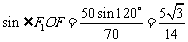 ,
,
所以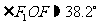 ,从而
,从而 .
.
 答
答 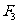 为
为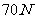 ,
,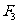 与
与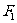 之间的夹角是
之间的夹角是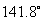 .
.
[例2]半圆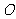 的直径为
的直径为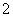 ,
,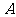 为直径延长线上的一点,
为直径延长线上的一点,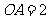 ,
,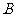 为半圆上任意一点,以
为半圆上任意一点,以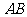 为一边作等边三角形
为一边作等边三角形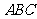 .问:点
.问:点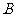 在什么位置时,四边形
在什么位置时,四边形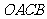 面积最大?
面积最大?
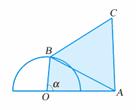
分析:四边形的面积由点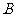 的位置唯一确定,而点
的位置唯一确定,而点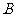 由
由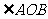 唯一确定,因此可设
唯一确定,因此可设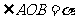 ,再用
,再用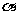 的三角函数来表示四边形
的三角函数来表示四边形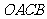 的面积.
的面积.
[解]设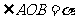 .在
.在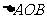 中,由余弦定理,得
中,由余弦定理,得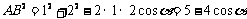 .
.
于是,四边形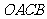 的面积为
的面积为
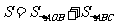
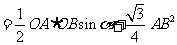
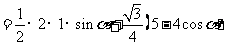
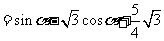
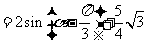 .
.
因为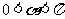 ,所以当
,所以当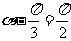 时,
时,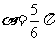 ,即
,即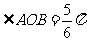 时,四边形
时,四边形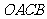 的面积最大.
的面积最大.
追踪训练一
1.利用正弦定理和余弦定理解决有关测量问题时,要注意分清仰角、俯角、张角和方位角等概念。
4.在⊿ABC中,若
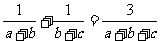 ,则B= 600 。
,则B= 600 。
提示:由条件知,
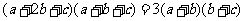 ,
,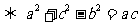
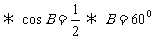
|

3.在锐角三角形ABC中,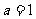 ,
, ,则边
,则边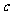 的取值范围是 ( C
)
的取值范围是 ( C
)
A
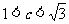 B
B 
C
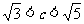 D
D 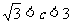
提示:分边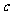 是最大边和不是最大边两种情况讨论,用余弦定理。
是最大边和不是最大边两种情况讨论,用余弦定理。
2.有一广告气球,直径为6m,放在公司大楼的上空,当行人仰望气球中心的仰角为300时,测得气球的视角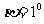 ,若
,若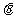 很小时可取
很小时可取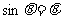 ,则估算该气球离地高度为( B )
,则估算该气球离地高度为( B )
 A 72 m
B 86 m
A 72 m
B 86 m
C 102 m D 118 m
1.在⊿ABC中,已知A=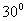 ,且
,且 ,则C的值为( C
)
,则C的值为( C
)
A 4 B 9 C 4或9 D 无解
3.如图,某人在高出海面600m的山上P处,测得海面上的航标A在正东,俯角为30°,航标B在南偏东60°,俯角为45°,求这两个航标间的距离.
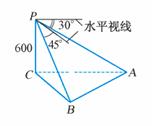
答案:这两个航标间的距离是600m.
[选修延伸]
[例4]三角形ABC中有两个角分别为300和450,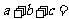
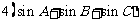 ,求⊿ABC的面积。
,求⊿ABC的面积。
[解]由条件知三角形的第三个角为1050,设三角形外接圆半径为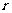 ,则
,则
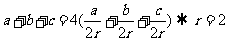
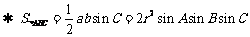
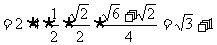 .
.
追踪训练二
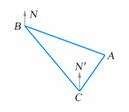
2.如图,货轮在海上以40nmile/h的速度由B向C航行,航行的方位角∠NBC=140°,A处有灯塔,其方位角∠NBA=110°,在C处观察灯塔A的方位角∠N′CA=35°,由B到C需航行0.5h,求C到灯塔A的距离.
答案: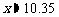 nmile
nmile
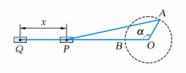
1. 曲柄连杆机构示意图如图所示.当曲柄OA在水平位置OB时,连杆端点P在Q的位置.当OA自OB按顺时针方向旋转α角时,P和Q之间的距离是xcm.已知OA=25cm,AP=125cm,根据下列条件,求x的值(精确到0.1cm): (1)α=50°; (2)α=135°.
答案:(1)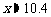 cm
cm
(2)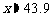 cm
cm
2.运用正弦定理、余弦定理解决实际问题的基本步骤是:
①分析:理解题意,弄清清与未知,画出示意图(一个或几个三角形);
②建模:根据书籍条件与求解目标,把书籍量与待求量尽可能地集中在有关三角形中,建立一个解斜三角形的数学模型;
③求解:利用正弦定理、余弦定理理解这些三角形,求得数学模型的解;
④检验:检验上述所求的解是否符合实际意义,从而得出实际问题的解。
[精典范例]

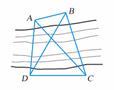 [例1]为了测量河对岸两点
[例1]为了测量河对岸两点 之间的距离,在河岸这边取点
之间的距离,在河岸这边取点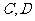 ,测得
,测得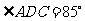 ,
,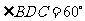 ,
,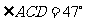 ,
,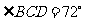 ,
, .设
.设 在同一平面内,试求
在同一平面内,试求 之间的距离(精确到
之间的距离(精确到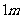 ).
).
[解]
在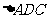 中,
中,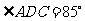 ,
,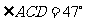 ,则
,则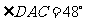 .又
.又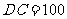 ,
,
由正弦定理,得
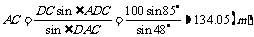 .在
.在 中,
中,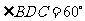 ,
,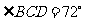 ,
,
则 .又
.又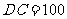 ,
,
由正弦定理,得
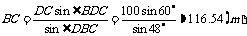 在
在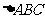 中,
中,
由余弦定理,得

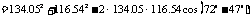
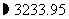 ,
,
所以
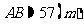
答  两点之间的距离约为
两点之间的距离约为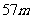 .
.
[例2]某渔轮在航行中不幸遇险,发出呼救信号,我海军舰艇在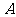 处获悉后,测出该渔轮在方位角为
处获悉后,测出该渔轮在方位角为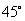 ,距离为
,距离为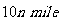 的
的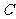 处,并测得渔轮正沿方位角为
处,并测得渔轮正沿方位角为 的方向,以
的方向,以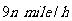 的速度向小岛靠拢,我海军舰艇立即以
的速度向小岛靠拢,我海军舰艇立即以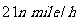 的速度前去营救.求舰艇的航向和靠近渔轮所需的时间(角度精确到
的速度前去营救.求舰艇的航向和靠近渔轮所需的时间(角度精确到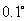 ,时间精确到
,时间精确到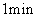 ).
).
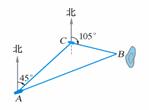
[解]设舰艇收到信号后
 在
在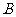 处靠拢渔轮,
处靠拢渔轮,
则 ,
, ,又
,又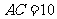 ,
,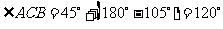 .
.
由余弦定理,得
 ,
,
即
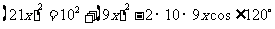 化简,得
化简,得
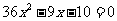 ,
,
解得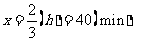 (负值舍去).
(负值舍去).
由正弦定理,得
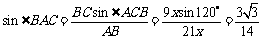 所以
所以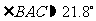 ,
,
方位角为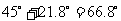 .
.
答 舰艇应沿着方向角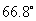 的方向航行,经过
的方向航行,经过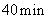 就可靠近渔轮.
就可靠近渔轮.
[例3]某海岛上一观察哨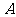 在上午
在上午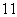 时测得一轮船在海岛北偏东
时测得一轮船在海岛北偏东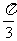 的
的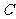 处,
处,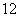 时
时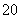 分测得轮船在海岛北偏西
分测得轮船在海岛北偏西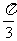 的
的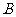 处,
处,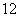 时
时 分轮船到达海岛正西方
分轮船到达海岛正西方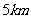 的
的 港口.如果轮船始终匀速前进,求船速.
港口.如果轮船始终匀速前进,求船速.
[解]设 ,船的速度为
,船的速度为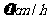 ,则
,则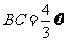 ,
,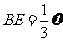 .
.
在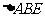 中,
中,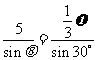 ,
,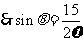 .
.
 在
在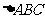 中,
中,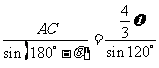 ,
,
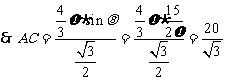 .
.
在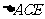 中,
中,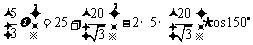 ,
,
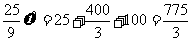 ,
,
 ,
,
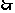 船的速度
船的速度 .
.
追踪训练一
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com