1．学会处理含字母系数的一元二次不等式恒成立问题　

2. 解关于x的不等式x²－ax+1>0

1. 解关于x的不等式ax²－(a+1)x+1>0

2．分类讨论不要重复和遗漏

追踪训练二

1.分类讨论标准的确定

(1).x²系数的正负或者为零的讨论

(2).与0的大小比较

(3).两根大小的比较．

2．已知关于x的不等式ax²+2x+6a<0的解集为{x| x <2或x>3}, 求a的值．

例2.解关于x的不等式x²－(a+1)x+a>0

例3：解关于x的不等式ax²－x+1>0

[解]

思维点拔：

1．不等式ax²+bx+2<0的解集为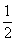{x| －<x<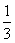}, 求a－b．

2．不等式(x-1)(x-a)<0的解集为　　

　　　　　　　　 　　　　　　　　　　。

[精典范例]

例1已知不等式x²+ax+b<0的解集为{x|－1<x<2}, 求不等式bx²－ax+1<0的解集。

[解]

变式：已知不等式b x²－ax+1 <0的解集为{x| x < 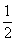－或x>1}, 求不等式x²+ax+b<0的解集．

思维点拔：

不等式与方程的关系是关键．从不等式的解方程的根韦达定理(或将根代入) 新不等式的解．

追踪训练一

1．不等式a(x-1)(x-2)<0的解集为

{x|x<1或x>2}则a与0的关系为：　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

2．会解一些简单的含参数的一元二次不等式．

[课堂互动]

自学评价