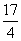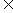1．已知不等式1≤－x²+x+a≤在x[-1,1]上时总成立，求实数a的取值范围．

2．分类讨论不要重复和遗漏．

追踪训练二

方程x²－mx-m+3=0的两根均在(-4,0)内，求m的取值范围．

[选修延伸]

不等式区间 [a,b]上恒成立问题

若不等式x²－2ax+a+6>0在x∈[-2,2]上时总成立，求实数a的取值范围．

思维点拔：

对于不等式f(x)≥M在x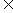[a,b]上恒成立，只需将其转化为f(x)在[a,b]上的最小值f(x)_min≥M即可．因此解决此题的关键是求f(x)在区间[a,b]上的最小值．

类似地，对于不等式f(x)≤M在x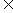[a,b]上恒成立，只需将其转化为f(x)在[a,b]上的最大值f(x)_max≤M即可．因此解决此题的关键是求f(x)在区间[a,b]上的最大值

追踪训练三

1．实根分布问题解题步骤

(1)化方程一边为零;

(2)设非零一边为函数f(x);

(3)画函数f(x)的符合题意的草图；

(4)根据草图列不等式组；

　(5)解不等式组．

2．已知函数f(x)=ax²+bx+c的图象过点(-1,0)是否存在常数a,b,c使不等式x≤f(x)≤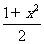对切实数x都成立？若存在，求出a,b,c的值，若不存在，说明理由．

例2. 分别求m的取值范围, 使方程x²－mx－m+3=0 的两根满足下列条件:

(1)两根都大于－5 ;

(2)一根大于0小于1 , 一根大于1小于2 .

例3：已知A={x|x²+(P+2)x+4=0}, M={x|x>0}, 若A∩M=φ, 求实数P的取值范围.

[解]

思维点拔：

1．当a为何值时, 不等式(a²－3a+2) x²+(a－1)x+2>0恒成立．

2。若ax²+bx+c>0解集为φ，则

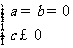或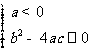

追踪训练一

1。若ax²+bx+c>0恒成立(即解集为R)，则

或

2．方程x²+(m-3)x+m=0的解集为，则m取值范围为　　　　

[精典范例]

例1:已知关于x不等式kx²-2x+6k<0的解集为R 求k的取值范围。

[解]

变式：已知关于x不等式kx²-2kx+6<0的解集为，求k的取值范围。

思维点拔：

1．不等式x²+2x+m²>0恒成立，则m取值范围为　　　　

2．学会处理含字母系数的一元二次不等式实根分布问题

[课堂互动]

自学评价