
6.[解析]解应用题的一般步骤是:审、设、列、解、验、答。正确找出题中的等量或不等关系是解题的关键。本题利用一次函数的增减性确定了总费用的最大值。
[答案](1)设这批赈灾物资运往 县的数量为
县的数量为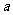 吨,运往
吨,运往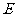 县的数量为
县的数量为 吨.
吨.
由题意,得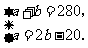 解得
解得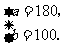
答:这批赈灾物资运往 县的数量为180吨,运往
县的数量为180吨,运往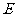 县的数量为100吨.
县的数量为100吨.
(2)由题意,得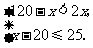
解得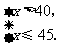 即
即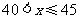 .
.
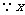 为整数,
为整数,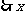 的取值为41,42,43,44,45.
的取值为41,42,43,44,45.
则这批赈灾物资的运送方案有五种.
具体的运送方案是:
方案一:A地的赈灾物资运往D县41吨,运往E县59吨;
B地的赈灾物资运往D县79吨,运往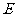 县21吨.
县21吨.
方案二:A地的赈灾物资运往D县42吨,运往E县58吨;
B地的赈灾物资运往D县78吨,运往E县22吨.
方案三:A地的赈灾物资运往D县43吨,运往E县57吨;
B地的赈灾物资运往D县77吨,运往E县23吨.
方案四:A地的赈灾物资运往D县44吨,运往E县56吨;
B地的赈灾物资运往D县76吨,运往E县24吨.
方案五:A地的赈灾物资运往D县45吨,运往E县55吨;
B地的赈灾物资运往D县75吨,运往E县25吨.
(3)设运送这批赈灾物资的总费用为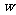 元.由题意,得
元.由题意,得
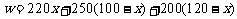
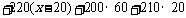
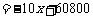 .
.
因为w随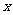 的增大而减小,且
的增大而减小,且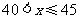 ,
,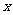 为整数.
为整数.
所以,当x=41时,w有最大值.则该公司承担运送这批赈灾物资的总费用最多为:w=60930(元).
5.[答案]解:设面值为2元的有x张,设面值为2元的有y张,依题意得
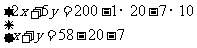
解得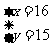
经检验,符合题意
答:面值为2元的有16张,设面值为2元的有15张.
4.[答案]解:(1)由租用甲种汽车x辆,则租用乙种汽车(8-x)辆
由题意得: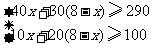
解得: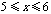
即共有2种租车方案:
第一种是租用甲种汽车5辆,乙种汽车3辆;
第二种是租用甲种汽车6辆,乙种汽车2辆.
(2)第一种租车方案的费用为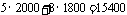 元;
元;
第二种租车方案的费用为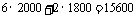 元
元
∴第一种租车方案更省费用.
3.[解析]通过表格当中的信息,我们可以利用列方程组来求出生产甲、乙两种产品的时间,然后利用列函数关系式表示出小王得到的总钱数,然后利用一次函数的增减性求出钱数的最大值.
[答案](1)解:设生产一件甲种产品需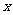 分,生产一件乙种产品需
分,生产一件乙种产品需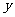 分,由题意得:
分,由题意得:
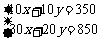 即
即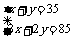
解这个方程组得:
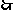 生产一件甲产品需要15分,生产一件乙产品需要20分.
生产一件甲产品需要15分,生产一件乙产品需要20分.
(2)解:设生产甲种产品用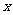 分,则生产乙种产品用
分,则生产乙种产品用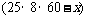 分,则生产甲种产品
分,则生产甲种产品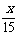 件,生产乙种产品
件,生产乙种产品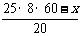 件.
件.
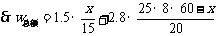
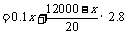
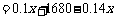
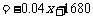
又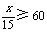 ,得
,得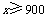
由一次函数的增减性,当 时
时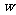 取得最大值,此时
取得最大值,此时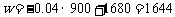 (元)
(元)
此时 甲有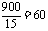 (件),
(件),
乙有: (件)
(件)
2.[答案]解:设康乃馨每支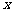 元,水仙花每支
元,水仙花每支 元
元
由题意得: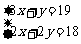 解得:
解得: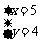
第三束花的价格为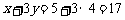
答:第三束花的价格是17元.
1.[解析]由天平的平衡得到巧克力和果冻重量之间的数量关系设每块巧克力的重量为x克,每块果冻的重量为y克,由题意列方程组得: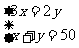 ,解方程组即可。
,解方程组即可。
[答案]20
10.( •河南))某校八年级举行英语演讲比赛,拍了两位老师去学校附近的超市购买笔记本作为奖品.经过了解得知,该超市的A、B两种笔记本的价格分别是12元和8元,他们准备购买者两种笔记本共30本.
(1) 如果他们计划用300元购买奖品,那么能卖这两种笔记本各多少本?
(2) 两位老师根据演讲比赛的设奖情况,决定所购买的A种笔记本的数量要少于B
种笔记本数量的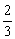 ,但又不少于B种笔记本数量的
,但又不少于B种笔记本数量的 ,如果设他们买A种笔记本n本,买这两种笔记本共花费w元.
,如果设他们买A种笔记本n本,买这两种笔记本共花费w元.
① 请写出w(元)关于n(本)的函数关系式,并求出自变量n的取值范围;
② 请你帮助他们计算,购买这两种笔记本各多少时,花费最少,此时的花费是多少元?
第1课时 方程(组)与不等式(组)问题
9.(•湖北省黄石市)某公司有A型产品40件,B型产品60件,分配给下属甲、乙两个商店销售,其中70件给甲店,30件给乙店,且都能卖完.两商店销售这两种产品每件的利润(元)如下表:
|
|
A型利润 |
B型利润 |
|
甲店 |
200 |
170 |
|
乙店 |
160 |
150 |
(1)设分配给甲店A型产品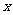 件,这家公司卖出这100件产品的总利润为W(元),求W关于
件,这家公司卖出这100件产品的总利润为W(元),求W关于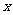 的函数关系式,并求出
的函数关系式,并求出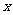 的取值范围;
的取值范围;
(2)若公司要求总利润不低于17560元,说明有多少种不同分配方案,并将各种方案设计出来;
(3)为了促销,公司决定仅对甲店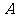 型产品让利销售,每件让利
型产品让利销售,每件让利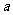 元,但让利后A型产品的每件利润仍高于甲店B型产品的每件利润.甲店的B型产品以及乙店的A,B型产品的每件利润不变,问该公司又如何设计分配方案,使总利润达到最大?
元,但让利后A型产品的每件利润仍高于甲店B型产品的每件利润.甲店的B型产品以及乙店的A,B型产品的每件利润不变,问该公司又如何设计分配方案,使总利润达到最大?
8.(•达州市)“5·12”汶川大地震震惊全世界,面对人类特大灾害,在党中央国务院的领导下,全国人民万众一心,众志成城,抗震救灾.现在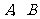 两市各有赈灾物资500吨和300吨,急需运往汶川400吨,运往北川400吨,从
两市各有赈灾物资500吨和300吨,急需运往汶川400吨,运往北川400吨,从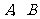 两市运往汶川、北川的耗油量如下表:
两市运往汶川、北川的耗油量如下表:
|
|
汶川(升/吨) |
北川(升/吨) |
|
A市 |
0.5 |
0.8 |
|
B市 |
1.0 |
0.4 |
(1)若从A市运往汶川的赈灾物资为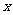 吨,求完成以上运输所需总耗油量y(升)与x(吨)的函数关系式.
吨,求完成以上运输所需总耗油量y(升)与x(吨)的函数关系式.
(2)请你设计一种最佳运输方案,使总耗油量最少,并求出完成以上方案至少需要多少升油?
7.(•宁波市)5月1日,目前世界上最长的跨海大桥--杭州湾跨海大桥通车了.通车后,苏南A地到宁波港的路程比原来缩短了120千米.已知运输车速度不变时,行驶时间将从原来的3时20分缩短到2时.
(1)求A地经杭州湾跨海大桥到宁波港的路程.
(2)若货物运输费用包括运输成本和时间成本,已知某车货物从A地到宁波港的运输成本是每千米1.8元,时间成本是每时28元,那么该车货物从A地经杭州湾跨海大桥到宁波港的运输费用是多少元?
(3)A地准备开辟宁波方向的外运路线,即货物从A地经杭州湾跨海大桥到宁波港,再从宁波港运到B地.若有一批货物(不超过10车)从A地按外运路线运到B地的运费需8320元,其中从A地经杭州湾跨海大桥到宁波港的每车运输费用与(2)中相同,从宁波港到B地的海上运费对一批不超过10车的货物计费方式是:一车800元,当货物每增加1车时,每车的海上运费就减少20元,问这批货物有几车?









类型之三 借助方程、不等式或函数求极值问题
“在生活中学数学,到生活中用数学”,是新课标所倡导的一个主旨之一,我们可以利用数学知识求解生活中的实际问题,有些问题可以借助于方程、不等式和函数知识来求一些问题的极值问题,这就要求我们建立恰当的数学模式来解决. 
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com