
1.(2002年上海高考题)一般地,家庭用电量(千瓦时)与气温(℃)有一定的关系.图(1)表示某年12个月中每月的平均气温,图(2)表示某家庭在这年12个月中每月的用电量.根据这些信息,以下关于该家庭用电量与气温间关系的叙述中,正确的是:( )
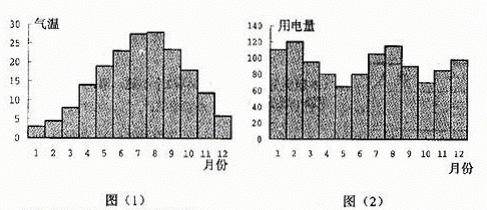
(A) 气温最高时,用电量最多.
(B) 气温最低时,用电量最少.
(C) 当气温大于某一值时,用电量随气温增高而增加.
(D) 当气温小于某一值时,用电量随气温降低而增加.
2.(2003年上海春季高考)在一次人才招聘会上,有A、B两家公司分别开出他们的工资标准:A公司允诺第一年月工资数为1500元,以后每年月工资比上一年月工资增加230元;B公司允诺第一年月工资数为2000元,以后每年月工资在上一年的月工资的基础上递增5%.设某人年初被A、B两家公司同时录取,试问:
(Ⅰ)若某人分别在A公司或B公司连续工作n年,则他在第n年的月工资收入分别是多少?
(Ⅱ)该人打算连续在一家公司工作10年,仅从工资收入总量较多作为应聘的标准(不计其它因素),该人应该选择那家公司,为什么?
(Ⅲ)在A公司工作比在B公司工作的月工资收入最多可以多多少元?(精确到1元),并说明理由.
[答案与提示:1.(Ⅰ)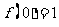 表示没有用水清洗时,蔬菜上的农药量将保持原样;(Ⅱ)函数
表示没有用水清洗时,蔬菜上的农药量将保持原样;(Ⅱ)函数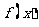 应该满足的条件和具有的性质是:
应该满足的条件和具有的性质是: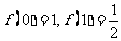 且
且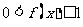 ,
,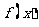 在
在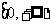 上单调递减;(Ⅲ)
上单调递减;(Ⅲ)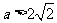 时,两次清洗后残留的农药量较少,
时,两次清洗后残留的农药量较少,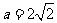 时,效果相同,
时,效果相同,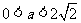 时,一次清洗残留的农药量较少. 2. (Ⅰ)在A公司和B公司第n年的月收入分别为
时,一次清洗残留的农药量较少. 2. (Ⅰ)在A公司和B公司第n年的月收入分别为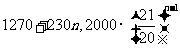 ;(Ⅱ)应选择A公司;(Ⅲ)826元.]
;(Ⅱ)应选择A公司;(Ⅲ)826元.]
1.(2001年上海高考题)用水清洗一堆蔬菜上残留的农药,对用一定量的水清洗一次的效果作如下假定:用一个单位量的水可洗掉蔬菜上残留农药量的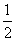 ,用水越多洗掉的农药量也越多,但总还有农药残留在蔬菜上.设用
,用水越多洗掉的农药量也越多,但总还有农药残留在蔬菜上.设用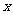 单位量的水清洗一次后,蔬菜上残留的农药量与本次清洗前残留的农药量之比为函数
单位量的水清洗一次后,蔬菜上残留的农药量与本次清洗前残留的农药量之比为函数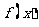 .
.
(Ⅰ)试规定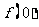 的值,并解释其实际意义;
的值,并解释其实际意义;
(Ⅱ)试根据假定写出函数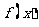 应该满足的条件和具有的性质;
应该满足的条件和具有的性质;
(Ⅲ)设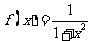 ,现有
,现有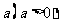 单位量的水,可以清洗一次,也可以把水平均分成2份后清洗两次,试问用哪种方案清洗后蔬菜上残留的农药量比较少?说明理由.
单位量的水,可以清洗一次,也可以把水平均分成2份后清洗两次,试问用哪种方案清洗后蔬菜上残留的农药量比较少?说明理由.
3.(2002北京春季高考22题)已知某椭圆的焦点是F1(–4,0)、F2(4,0),过点F2并垂直于x轴的直线与椭圆的一个交点为B,且|F1B|+|F2B|=10,椭圆上不同的两点A(x1,y1)、C(x2,y2)满足条件:|F2A|、|F2B|、|F2C|成等差数列.
(Ⅰ)求该椭圆方程;
(Ⅱ)求弦AC中点的横坐标;
(Ⅲ)设弦AC的垂直平分线的方程为y=kx+m,求m的取值范围.
[答案与提示:1。(Ⅰ)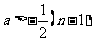 ;(Ⅱ)略。 2。(Ⅰ)当
;(Ⅱ)略。 2。(Ⅰ)当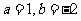 时,函数
时,函数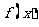 的两个不动点为
的两个不动点为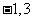 ;(Ⅱ)
;(Ⅱ)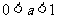 ;(Ⅲ)
;(Ⅲ)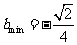 。 3。(Ⅰ)
。 3。(Ⅰ)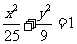 ;(Ⅱ)
;(Ⅱ)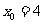 ;(Ⅲ)
;(Ⅲ)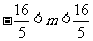 。]
。]
2.(2002年上海春季高考22题)对于函数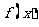 ,若存在
,若存在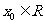 ,使得
,使得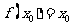 成立,则称
成立,则称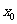 为
为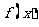 的不动点。已知函数
的不动点。已知函数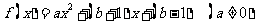 。
。
(Ⅰ)当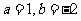 时,求函数
时,求函数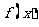 的不动点;
的不动点;
(Ⅱ)若对任意实数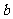 ,函数
,函数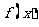 恒有两个相异的不动点。求
恒有两个相异的不动点。求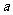 的取值范围;
的取值范围;
(Ⅲ)在(Ⅱ)的条件下,若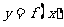 图像上
图像上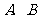 两点的横坐标是函数
两点的横坐标是函数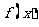 的不动点,且
的不动点,且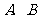 两点关于直线
两点关于直线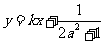 对称,求
对称,求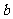 的最小值。
的最小值。
1.(1990年全国高考题)设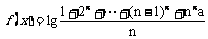 ,其中a是实数,n是任意给定的自然数,且n≥2.
,其中a是实数,n是任意给定的自然数,且n≥2.
(Ⅰ)如果f(x)当x∈(-∞,1]时有意义,求a的取值范围;
(Ⅱ)如果a∈(0,1],证明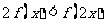 当x≠0时成立.
当x≠0时成立.
2.(2002北京高考题)已知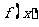 是定义在R上的不恒为零的函数,且对于任意的
是定义在R上的不恒为零的函数,且对于任意的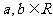 都满足:
都满足: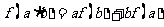
(Ⅰ)求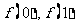 的值;
的值;
(Ⅱ)判断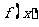 的奇偶性,并证明你的结论;
的奇偶性,并证明你的结论;
(Ⅲ)若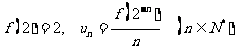 ,求数列
,求数列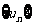 的前
的前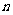 项的和
项的和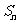 .
.
[答案与提示:1.(Ⅰ)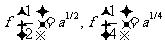 ;(Ⅱ)略;(Ⅲ)
;(Ⅱ)略;(Ⅲ)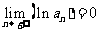 .
2.(Ⅰ)
.
2.(Ⅰ)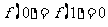 ;(Ⅱ)奇函数;(Ⅲ)
;(Ⅱ)奇函数;(Ⅲ)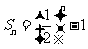 .]
.]
1.(2001年全国高考题)设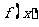 是定义在R上的偶函数,其图像关于直线
是定义在R上的偶函数,其图像关于直线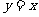 对称,对任意
对称,对任意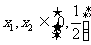 都有
都有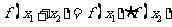 ,且
,且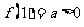 .
.
(Ⅰ)求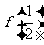 及
及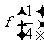 ;
;
(Ⅱ)证明: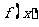 是周期函数;
是周期函数;
(Ⅲ)记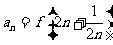 ,求
,求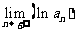 .
.
3.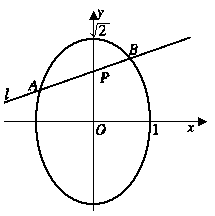 (2001年上海春季高考)已知椭圆
(2001年上海春季高考)已知椭圆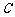 的方程为
的方程为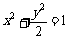 ,点
,点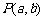 的坐标满足
的坐标满足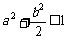 .过点
.过点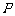 的直线
的直线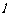 与椭圆交于
与椭圆交于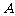 、
、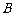 两点,点
两点,点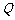 为线段
为线段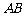 的中点,求:
的中点,求:
(1)点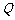 的轨迹方程;
的轨迹方程;
(2)点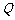 的轨迹与坐标轴的交点的个数.
的轨迹与坐标轴的交点的个数.
[答案与提示:1.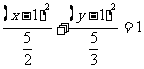
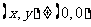 ; 2.
; 2.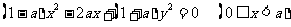 ; 3.(1)点Q的轨迹方程为
; 3.(1)点Q的轨迹方程为 ; (2)略.]
; (2)略.]
2.
(1999年全国高考题)如图,给出定点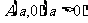 和直线
和直线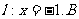 是直线
是直线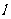 上的动点,
上的动点,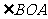 的角平分线交
的角平分线交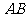 于点
于点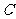 .求点
.求点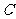 的轨迹方程,并讨论方程表示的曲线类型与
的轨迹方程,并讨论方程表示的曲线类型与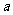 值的关系.
值的关系.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com