
1.已知等差数列的通项公式为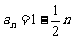 ,求它的首项和公差,并画出它的图象.
,求它的首项和公差,并画出它的图象.
[答案]略
2.已知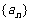 是等差数列,若
是等差数列,若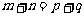 ,则
,则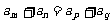
[精典范例]
[例1]已知等差数列{an}的通项公式为an=2n-1,求首项a1和公差d,并画出图像。
[解]
[答案]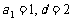
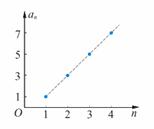
等差数列的通项公式an=2n-1是关于n的一次式,从图象上看,表示这个数列的各点(n,an)均在直线y=2x-1上。
[例2](1)在等差数列{an}中,是否有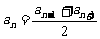 (n≥2)?
(n≥2)?
(2)在数列{an}中,如果对于任意的正整数n(n≥2),都有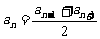 ,那么数列{an}一定是等差数列吗?
,那么数列{an}一定是等差数列吗?
[解]
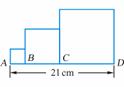
[例3]如图,三个正方形的边AB,BC,CD的长组成等差数列,且AD=21cm,这三个正方形的面积之和是179cm2.
(1)求AB,BC,CD的长;
 (2)以AB,BC,CD的长为等差数列的前三项,以第10项为边长的正方形的面积是多少?
(2)以AB,BC,CD的长为等差数列的前三项,以第10项为边长的正方形的面积是多少?
[解]
(1)设公差为d(d>0),BC=x,则AB=x-d,CD=x+d.由题意得
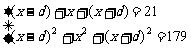
解得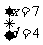 或
或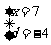 (舍去)
(舍去)
AB=3(cm),BC=7(cm),CD=11(cm)
(2)正方形的边长组成首项是3,公差是4的等差数列{an},所以
a10=3+(10-1)×4=39.
a210=392=1521(cm2).
所求正方形的面积为1521cm2.
[追踪训练一]:
1.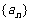 是等差数列
是等差数列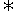
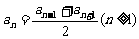
2.初步通过数列的下标研究数列。
[自学评价]
1. 体会等差数列与一次函数的关系;
8.若x≠y,两个数列:x,a1,a2,a3,y和x,b1,b2,b3,b4,y都是等差数列,求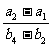 的值.
的值.
[解] 设两个等差数列的公差分别为d1、d2,即求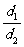 ,由已知得
,由已知得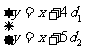
即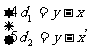 解得
解得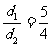 ,
,
即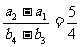
|
5.已知数列{an}满足an+12=an2+4,且a1=1,an>0,求an.
[解] 由an+12=a2n+4即an+12-an2=4∴数列{an2}构成等差数列.an2=a12+(n-1)d=12+(n-1)·4=4n-3
又an>0∴an=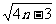
4.已知等差数列的第10项为23,第25项为-22,则此数列的通项公式为an=-3n+53_.
3.如果等差数列{an}的第5项为5,第10项为-5,那么此数列的第一个负数项是第__8_项.
2.在等差数列{an}中,若a3+a4+a5+a6+a7=450,则a2+a8等于( C )
A.45 B.75 C.180 D.300
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com