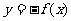
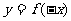
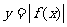
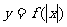
作业：作出下列函数的图象：

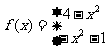
1.　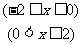 　　　2.

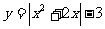
解：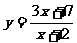

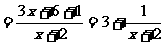
可由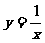的图象向左平移两个单位得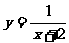的图象，再向上平移三个单位得 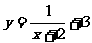的图象。

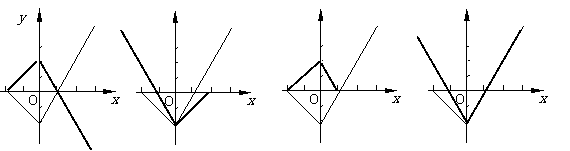
(A)　　　　　　　　 (B)　　　　　　　 (C)　　　　　　 (D)

解：(A)中定义域为[0,1]　 (C)中值域[0,3]¹N　 (D)中x的值(如x=1)有两个y值与之对应，不是函数 　∴只有(B)正确。

　　　　 (A)　　　　　　　 (B)　　　　　　 (C)　　　　　　　 (D)

　　 　解： A、C图中t=0时d=0即该生一出家门便进家门(与学校距离为0)应排除，B、D中因该生一开始就跑步与学校距离迅速减小。故应选D。

4．本课的例题选择可根据自己所教学生的实际情况，下面几个备用题可供参考．

题目1过圆O：x²+y²=4与y轴正半轴的交点A作这圆的切线l，M为l上任一点，过M作圆O的另一条切线，切点为Q，求点M在直线l上移动时，△MAQ垂心的轨迹方程．

(选题目的：熟练用代入法求动点的轨迹方程，活用平几简化计算．)

解　 如图2-81所示．P为△AMQ的垂心，连OQ，则四边形AOQP为菱形，所以|PQ|=|OA|=2，设P(x₁，y₁)，Q(x₀，y₀)．于是有x₀=x₁且

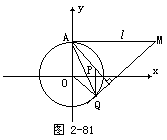
题目2若抛物线y=x²上存在关于直线y=m(x-3)对称的两点，求实数m的取值范围．

解　 (如图2-82)设抛物线上两点A(x₁，y₁)，B(x₂，y₂)关于直线

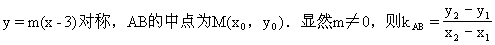
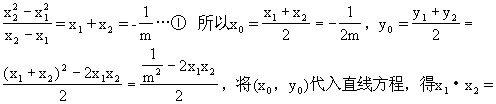
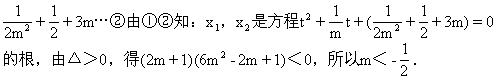
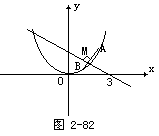
(选题目的：结合对称问题，训练反证法的应用．)

此题证法很多．下面给一种证法供参考．

证明　 如图2-83，若P、Q两点关于y=x对称，可设P(a，b)、

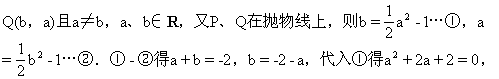
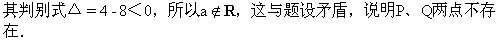
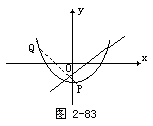
3．习题课的一个中心就是解题，怎样才能让学生做尽可能少的题，从而让学生掌握通理通法，这是一个值得研究和探讨的问题．本节课采取了让学生把题目进行一题多变，一题多解，从中使学生悟出一些解题办法和规律，从而达到尽可能做少量的题，而达到获取尽可能多的知识、方法和规律的目的，真正提高学生的分析问题、提出问题、解决问题的能力．解决当前学生课业负担过重的问题，根除题海战术给学生带来的危害．

2．这节课自始至终贯穿数形结合的数学思想，让学生在脑海里留下一个深刻的印象，就是对称问题，归根结底都可以化成点关于直线的对称问题，即可用方程组去解决．反过来，一直线与一曲线的方程组消元后得到一元二次方程，若这二次方程的判别式大于零，也可得直线与曲线有两个交点，这种从形到数，再由数到形的转化为我们处理解析几何问题带来了便利．在解题时，只有站在一定的高度上去处理问题，思路才能开阔，方法才能灵活，学生的能力才能真正的得到培养，同时水平才能提高得较快．

1．这节课是一节专题习题课，也可以认为是复习题，通过讨论对称问题把有关的知识进行复习，最重要的是充分突出以学生为主体．让学生讨论和发言，就是让学生参加到数学教学中来，使学生兴趣盎然，思维活跃，同时对自己也充满了信心．这样，才有利于发挥学生的主动性，有利于培养学生的独立思考的习惯，发展学生的创造性和思维能力．因此，在数学教学中要有一定的时间让学生充分地发表自己的见解，从而来提高他们的兴趣，发展他们的能力．

4．已知曲线C：y=-x²+x+2关于点(a，2a)对称的曲线是C′，若C与C′有两个不同的公共点，求a的取值范围．(-2＜a＜1)

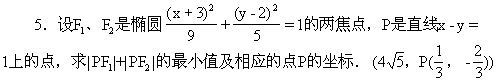
设计说明

3．若光线从点A(-3，5)射到直线3x-4y+4=0之后，反射到点B(3，