
3. 函数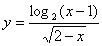 的定义域是
。
的定义域是
。
2. 已知复数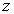 满足
满足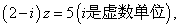 则
则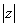 =
=
1.设集合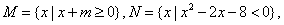 若
若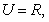 且
且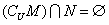 , 则实数m的取值范围是
。
, 则实数m的取值范围是
。
20.(本题满分16分)
矩形ABCD中,AB =2,AD = ,H是AB中点,以H为直角顶点作矩形的内接直角三角形HEF,其中E,F分别落在线段BC和线段AD上,如图.记∠BHE为θ,记Rt△EHF的周长为 l.
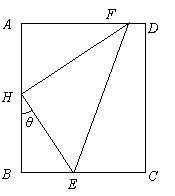 ⑴试将 l 表示为 θ 的函数;
⑴试将 l 表示为 θ 的函数;
⑵求 l 的最小值及此时的 θ.
19.(本题满分16分)
已知二次函数f (x) = x2 −ax + a (x∈R)同时满足:
①不等式 f (x) ≤ 0的解集有且只有一个元素;
②在定义域内存在0 < x1 < x2,使得不等式f (x1) > f (x2)成立.
设数列{an}的前 n 项和Sn = f (n).
(1)求函数f (x)的表达式;
(2)求数列{an}的通项公式;
(3)在各项均不为零的数列{cn}中,若ci·ci+1 < 0,则称ci,ci+1为这个数列{cn}一对变号项.令cn = 1 − (n为正整数),求数列{cn}的变号项的对数.
18.(本题满分15分)
已知a∈R,函数f (x) = − x3 + ax2 + 2ax (x∈R).
(Ⅰ)当a = 1时,求函数f (x)的单调递增区间;
(Ⅱ)函数 f (x) 能否在R上单调递减,若是,求出 a的取值范围;若不能,请说明理由;
(Ⅲ)若函数f (x)在[−1,1]上单调递增,求a的取值范围.
17.(本题满分15分)
已知向量= (cos ,sin ),= (cos ,−sin ), = (,−1) ,其中x∈R.
(I)当⊥时,求x值的集合;
(Ⅱ)求| − |的最大值.
16.(本题满分14分)
某单位用2160万元购得一块空地,计划在该地块上建造一栋至少10层,每层2000平方米的楼房。经测算,如果将楼房建为x(x ≥ 10)层,则每平方米的平均建筑费用为560 + 48x(单位:元).
⑴写出楼房平均综合费用y关于建造层数x的函数关系式;
⑵该楼房应建造多少层时,可使楼房每平方米的平均综合费用最少?最少值是多少?
(注:平均综合费用 = 平均建筑费用 + 平均购地费用,平均购地费用 = )
15.(本题满分14分)
已知函数f (x) = 的定义域集合是A,函数 g(x) = lg [x2 − (2a + 1)x + a2 + a]的定义域集合是B.
(1)求集合A,B.
(2)若A B = B,求实数a的取值范围.
B = B,求实数a的取值范围.
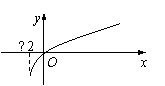
14.已知函数f (x) 的定义域为[−2,+∞),部分对应值如下左表,f ' (x) 为f (x) 的导函数,函数y = f ' (x)的图象如下右图所示,若两正数a,b满足f (2a + b) < 1,则 的取值范围是 ▲ .
|
x |
−2 |
0 |
4 |
|
f (x) |
1 |
−1 |
1 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com