
5.将参数方程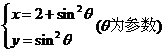 化为普通方程为
.
化为普通方程为
.
4.已知点P为椭圆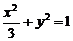 在第一象限部分上的点,则
在第一象限部分上的点,则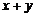 的最大值等于 .
的最大值等于 .
3.直线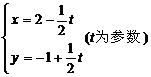 被圆
被圆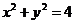 截得的弦长为______________.
截得的弦长为______________.
2.已知曲线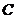 的参数方程是
的参数方程是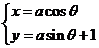 (
(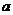 为参数),则普通方程为
.
为参数),则普通方程为
.
1.若直线的参数方程为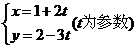 ,则直线的斜率为______________.
,则直线的斜率为______________.
20.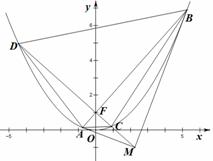 (13分)已知抛物线
(13分)已知抛物线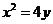 的焦点为
的焦点为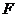 ,过焦点
,过焦点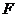 且不平行于x轴的动直线
且不平行于x轴的动直线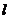 交抛物线于
交抛物线于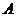 ,
,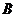 两点,抛物线在
两点,抛物线在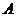 、
、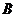 两点处的切线交于点
两点处的切线交于点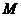 .
.
(Ⅰ)求证: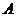 ,
,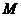 ,
,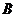 三点的横坐标成等差数列;
三点的横坐标成等差数列;
(Ⅱ)设直线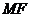 交该抛物线于
交该抛物线于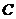 ,
,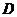 两点,求四边形
两点,求四边形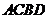 面积的最小值.
面积的最小值.
解:(Ⅰ)由已知,得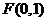 ,显然直线
,显然直线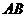 的斜率存在且不得0,
的斜率存在且不得0,
则可设直线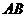 的方程为
的方程为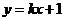 (
(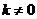 ),
),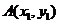 ,
,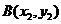 ,
,
由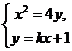 消去
消去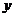 ,得
,得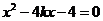 ,显然
,显然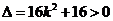 .
.
所以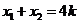 ,
,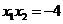 . ………………………………………………2分
. ………………………………………………2分
由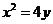 ,得
,得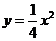 ,所以
,所以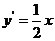 ,
,
所以,直线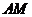 的斜率为
的斜率为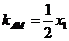 ,
,
所以,直线 的方程为
的方程为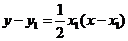 ,又
,又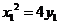 ,
,
所以,直线 的方程为
的方程为 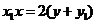 ①。………………………………4分
①。………………………………4分
同理,直线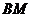 的方程为
的方程为 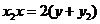 ②。………………………………5分
②。………………………………5分
②-①并据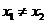 得点M的横坐标
得点M的横坐标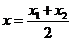 ,
,
即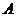 ,
,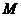 ,
,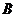 三点的横坐标成等差数列。 …………………………………7分
三点的横坐标成等差数列。 …………………………………7分
(Ⅱ)由①②易得y=-1,所以点M的坐标为(2k,-1)(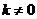 )。
)。
所以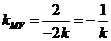 ,
,
则直线MF的方程为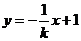 , …………………………………………8分
, …………………………………………8分
设C(x3,y3),D(x4,y4)
由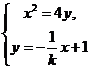 消去
消去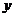 ,得
,得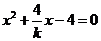 ,显然
,显然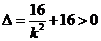 ,
,
所以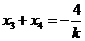 ,
,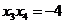 。
…………………………………………9分
。
…………………………………………9分
又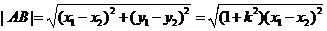
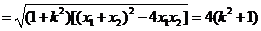 。…………10分
。…………10分
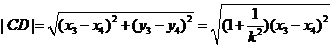
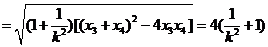 。……………………11分
。……………………11分
因为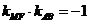 ,所以
,所以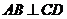 ,
,
所以,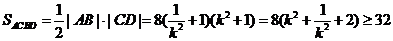 ,
,
当且仅当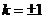 时,四边形
时,四边形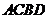 面积的取到最小值
面积的取到最小值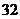 。……………………13分
。……………………13分
19.(14分)已知数列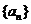 的前n项和为
的前n项和为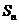 ,
,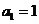 ,
,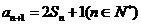 ,等差数列
,等差数列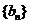 中,
中,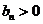
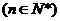 ,且
,且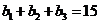 ,又
,又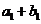 、
、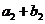 、
、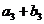 成等比数列.
成等比数列.
(Ⅰ)求数列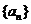 、
、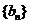 的通项公式;
的通项公式;
(Ⅱ)求数列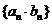 的前n项和
的前n项和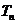 .
.
解:(Ⅰ)∵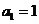 ,
,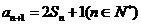 ,
,
∴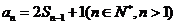 ,
,
∴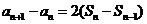 ,
,
∴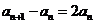 ,
,
∴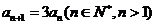 …………………………2分
…………………………2分
而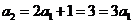 ,∴
,∴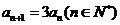
∴数列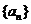 是以1为首项,3为公比的等比数列,
是以1为首项,3为公比的等比数列,
∴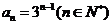 …………………………4分
…………………………4分
∴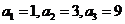 ,
,
在等差数列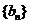 中,∵
中,∵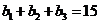 ,∴
,∴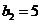 。
。
又因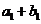 、
、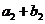 、
、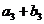 成等比数列,设等差数列
成等比数列,设等差数列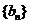 的公差为d,
的公差为d,
∴(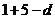 )
)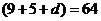 ………………………………6分
………………………………6分
解得d=-10,或d=2, ∵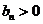
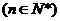 ,∴舍去d=-10,取d=2, ∴b1=3,
,∴舍去d=-10,取d=2, ∴b1=3,
∴bn=2n+1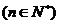 ,
………………………………8分
,
………………………………8分
(Ⅱ)由(Ⅰ)知
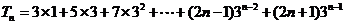 ①
①
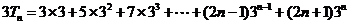 ②………………10分
②………………10分
① -②得
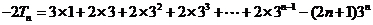 ……………12分
……………12分
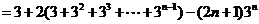
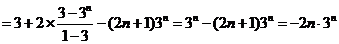 ,
,
∴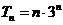 ………………………………………………………………14分
………………………………………………………………14分
18.(14分)已知函数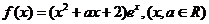 .
.
(Ⅰ)当a=0时,求函数f(x)的图像在点A(1,f(1))处的切线方程;
(Ⅱ)若f(x)在R上单调,求a的取值范围;
(Ⅲ)当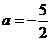 时,求函数f(x)的极小值。
时,求函数f(x)的极小值。
解: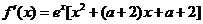
(Ⅰ)当a=0时,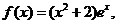
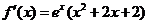 ,………………2分
,………………2分
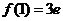 ,
,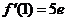 ,
,
∴函数f(x)的图像在点A(1,f(1))处的切线方程为y-3e=5e(x-1),
即5ex-y-2e=0 …………………………………………………………4分
(Ⅱ)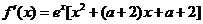 ,
,
考虑到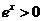 恒成立且
恒成立且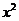 系数为正,
系数为正,
∴f(x)在R上单调等价于 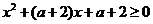 恒成立.
恒成立.
∴(a+2)2-4(a+2)£0,
∴-2£a£2 , 即a 的取值范围是[-2,2],……………………8分
(若得a的取值范围是(-2,2),可扣1分)
(Ⅲ)当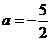 时,
时, 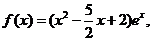
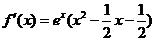 ,
,
………………………………………………………………10分
令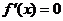 ,得
,得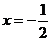 ,或x=1,
,或x=1,
令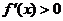 ,得
,得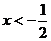 ,或x>1,
,或x>1,
令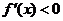 ,得
,得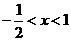 .
………………………………12分
.
………………………………12分
x,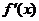 ,f(x)的变化情况如下表
,f(x)的变化情况如下表
|
X |
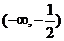 |
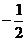 |
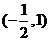 |
1 |
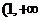 ) ) |
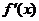 |
+ |
0 |
- |
0 |
+ |
|
f(x) |
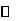 |
极大值 |
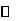 |
极小值 |
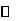 |
所以,函数f(x)的极小值为f(1)=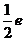 ……………………………………14分
……………………………………14分
17.(13分)在某次抽奖活动中,一个口袋里装有5个白球和5个黑球,所有球除颜色外无任何不同,每次从中摸出2个球,观察颜色后放回,若为同色,则中奖。
(Ⅰ)求仅一次摸球中奖的概率;
(Ⅱ)求连续2次摸球,恰有一次不中奖的概率;
(Ⅲ)记连续3次摸球中奖的次数为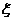 ,求
,求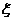 的分布列。
的分布列。
解:(Ⅰ)设仅一次摸球中奖的概率为P1,则P1=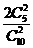 =
=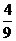 ……………………3分
……………………3分
(Ⅱ)设连续2次摸球(每次摸后放回),恰有一次不中奖的概率为P2,则
P2=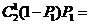
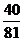 ………………………………………………7分
………………………………………………7分
(Ⅲ)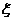 的取值可以是0,1,2,3
的取值可以是0,1,2,3
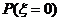 =(1-
=(1-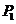 )3=
)3=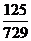 ,
,
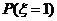 =
=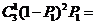
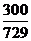 =
=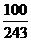 ,
,
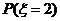 =
=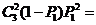 =
=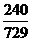 =
=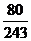 ,
,
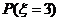 =
=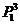 =
=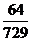
所以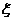 的分布列如下表
的分布列如下表
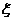 |
0 |
1 |
2 |
3 |
|
P |
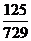 |
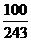 |
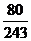 |
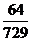 |
………………………………………………………13分
16.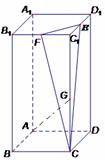 (14分)在正四棱柱
(14分)在正四棱柱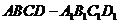 中,E,F分别是
中,E,F分别是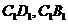 的中点,G为
的中点,G为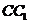 上任一点,EC与底面ABCD所成角的正切值是4.
上任一点,EC与底面ABCD所成角的正切值是4.
(Ⅰ)求证:AG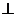 EF;
EF;
(Ⅱ)确定点G的位置,使AG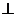 面CEF,并说明理由;
面CEF,并说明理由;
(Ⅲ)求二面角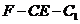 的余弦值。
的余弦值。
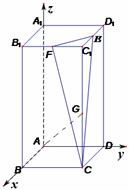 解:∵
解:∵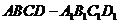 是正四棱柱
是正四棱柱
∴ABCD是正方形,设其边长为2a,ÐECD是EC与底面所成的角。而ÐECD=ÐCEC1, ∴CC1=4EC1=4a.……………1分
以A为原点,AB、AD、AA1所在的直线分别为x轴,y轴,z轴,建立如图所示的直角坐标系。
则A(0,0,0),B(2a,0,0),C(2a,2a,0),D(0,2a,0),
A1(0,0,4a),B1(2a,0,4a),C1(2a,2a,4a),D1(0,2a,4a),
E(a,2a,4a),F(2a,a,4a),设G(2a,2a,b)(0<b<4a)………………3分
(Ⅰ)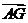 =(2a,2a,b),
=(2a,2a,b),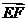 =(a,-a,0),
=(a,-a,0),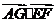 =2a2-2a2+0=0,
=2a2-2a2+0=0,
∴AG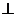 EF ……………………………………………………6分
EF ……………………………………………………6分
(Ⅱ)由(Ⅰ)知,使AG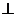 面CEF,只需AG
面CEF,只需AG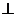 CE,
CE,
只需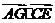 =(2a,2a,b)×(-a,0,4a)=-2a2+4ab=0,
=(2a,2a,b)×(-a,0,4a)=-2a2+4ab=0,
∴b=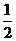 a,即CG=
a,即CG=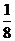 CC1时,AG
CC1时,AG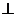 面CEF。………………10分
面CEF。………………10分
(Ⅲ)由(Ⅱ)知,当G(2a,2a,
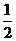 a)时,
a)时,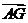 是平面CEF的一个法向量,
是平面CEF的一个法向量,
由题意可得,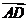 是平面CEC1的一个法向量,
是平面CEC1的一个法向量,
设二面角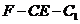 的大小为q,
的大小为q,
则cosq=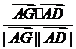 =
=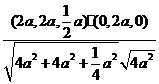 =
=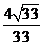 ,
,
二面角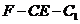 的余弦值为
的余弦值为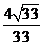 . …………………………14分
. …………………………14分
(运用综合法相应给分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com