
16. (本小题14分)如图:在四棱锥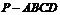 中,底面
中,底面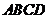 是菱形,
是菱形,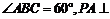 平面ABCD,
平面ABCD,
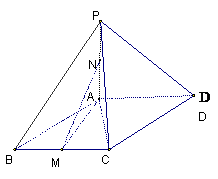 点
点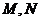 分别为
分别为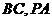 的中点,且
的中点,且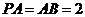 .
.
(I) 证明: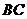 ⊥平面
⊥平面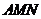 ;
;
(II)求三棱锥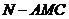 的体积;
的体积;
(III)在线段PD上是否存在一点E,使得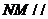 平面
平面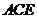 ;
;
若存在,求出PE的长;若不存在,说明理由.
15.(本小题14分)已知函数f
(x)=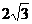 sinxcosx-2cos2x +1.
sinxcosx-2cos2x +1.
(Ⅰ) 求f (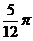 );
);
(Ⅱ) 求函数f (x)图象的对称轴方程.
14. 给出下列四个命题:
①若集合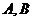 满足
满足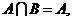 则
则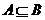 ;
;
②给定命题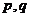 , 若“
, 若“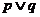 ”为真,则“
”为真,则“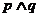 ”为真;
”为真;
③设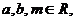 若
若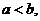 则
则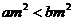 ;
;
④若直线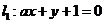 与直线
与直线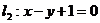 垂直,则
垂直,则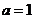 .
.
其中真命题的个数是_ _▲____.(写出所有真命题的个数)
13. 已知有公共焦点的椭圆与双曲线中心为原点,焦点在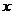 轴上,左右焦点分别为
轴上,左右焦点分别为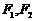 ,且它们在第一象限的交点为P,
,且它们在第一象限的交点为P,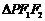 是以
是以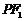 为底边的等腰三角形.若
为底边的等腰三角形.若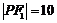 ,双曲线的离心率的取值范围为
,双曲线的离心率的取值范围为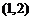 .则该椭圆的离心率的取值范围是_ ▲____.
.则该椭圆的离心率的取值范围是_ ▲____.
12. 已知程序框图如图所示,则执行该程序后输出的
结果是_ _▲____.
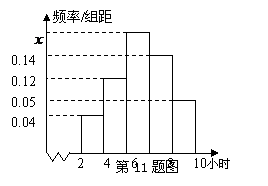
11.某校为了解高三同学寒假期间学习情况,抽查了100名同学,统计他们每天平均学习时间,绘成频率分布直方图(如图).则这100名同学中学习时间在6~8小时内的同学为_ _▲____人.

10. 在四边形ABCD中,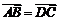 ,且
,且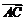 ·
·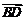 =0,则四边形ABCD是_ _▲___
=0,则四边形ABCD是_ _▲___
(填“矩形”、“菱形”、“直角梯形”、“等腰梯形”)
9. 直线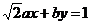 与圆
与圆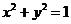 相交于A,B两点(其中
相交于A,B两点(其中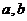 是实数),且
是实数),且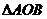 是直角三角形(O是坐标原点),则点P
是直角三角形(O是坐标原点),则点P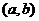 与点
与点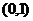 之间距离的最大值为_ _▲____.
之间距离的最大值为_ _▲____.
8. 已知不等式组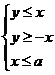 , 表示的平面区域的面积为4,点
, 表示的平面区域的面积为4,点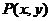 在所给平面区域内,
在所给平面区域内,
则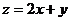 的最大值为_ _▲____.
的最大值为_ _▲____.
7.已知动点P到定点(2,0)的距离和它到定直线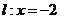 的距离相等,则点P的轨迹方程为 ▲ _
的距离相等,则点P的轨迹方程为 ▲ _
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com