
21、(本小题满分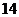 分)
分)
若存在实常数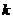 和
和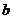 ,使得函数
,使得函数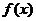 和
和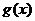 对其定义域上的任意实数
对其定义域上的任意实数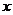 分别满
分别满
足: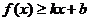 和
和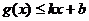 ,则称直线
,则称直线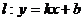 为
为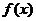 和
和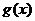 的“隔离直线”.
的“隔离直线”.
已知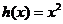 ,
,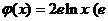 为自然对数的底数).
为自然对数的底数).
(1)求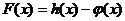 的极值;
的极值;
(2) 函数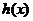 和
和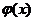 是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理
是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理
由.
20、(本小题满分14分)
已知二次函数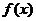 对任意
对任意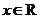 ,都有
,都有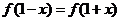 成立,设向量
成立,设向量 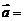 (sin x,2),
(sin x,2),
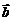 =(2sin x,
=(2sin x,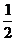 ),
),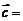 (cos2 x,1),
(cos2 x,1),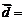 (1,2),当
(1,2),当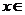 [0,
[0,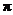 ] 时,求不等式 f(
] 时,求不等式 f(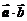 )>f(
)>f(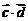 )的解集.
)的解集.
19、(本小题满分13分)
设函数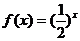 ,数列
,数列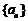 满足
满足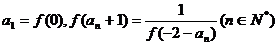
(1)求数列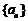 的通项公式;
的通项公式;
(2)令 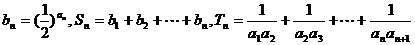 ,
,
试比较 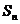 与
与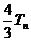 的大小,并加以证明.
的大小,并加以证明.
18、(本小题满分13分)
如图,四棱锥P-ABCD中,PA⊥平面ABCD,∠PBA = 45°, 底面ABCD为直角梯形,∠ABC = ∠BAD = 90°,PA = BC = AD.
(1) 求证:平面PAC⊥平面PCD;
(2) 在棱PD上是否存在一点E,使CE∥平面PAB ? 若存在,请确定E点的位置;若不存在,请说明理由.

17、(本小题满分13分)
已知函数 f ( x
) = 2a cos 2
x + b sin x cos x ,
且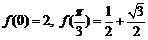 .
.
(1)求 f ( x ) 的最大值与最小值 ;
(2)若 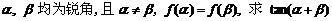 .
.
16、(本小题满分13分)
一个盒子中装有标号为1,2,3,4,5的5张标签,随机地选取两张标签,根据下列条件求两
张标签上的数字为相邻整数的概率:
(1) 标签的选取是无放回的;
(2) 标签的选取是有放回的.
15、在极坐标系中,方程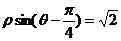 的直角坐标方程是 .
的直角坐标方程是 .
14、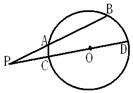 如图,已知⊙O的割线PAB交⊙O于A,B两点,割线PCD经过圆心,
如图,已知⊙O的割线PAB交⊙O于A,B两点,割线PCD经过圆心,
若PA = 3,AB = 4,PO = 5,则⊙O的半径为 _______________.
13、若 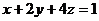 ,则
,则 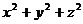 的最小值是 .
的最小值是 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com