
(二)指数函数的图象和性质
问题:你能类比前面讨论函数性质时的思路,提出研究指数函数性质的内容和方法吗?
研究方法:画出函数的图象,结合图象研究函数的性质.
研究内容:定义域、值域、特殊点、单调性、最大(小)值、奇偶性.
探索研究:
1.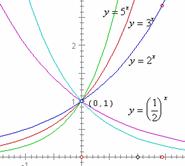 在同一坐标系中画出下列函数的图象:
在同一坐标系中画出下列函数的图象:
(1)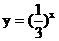
(2)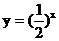
(3)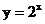
(4)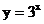
(5)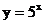
2.从画出的图象中你能发现函数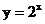 的图象和函数
的图象和函数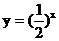 的图象有什么关系?可否利用
的图象有什么关系?可否利用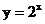 的图象画出
的图象画出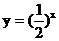 的图象?
的图象?
3.从画出的图象(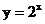 、
、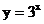 和
和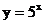 )中,你能发现函数的图象与其底数之间有什么样的规律?
)中,你能发现函数的图象与其底数之间有什么样的规律?
4.你能根据指数函数的图象的特征归纳出指数函数的性质吗?
|
图象特征 |
函数性质 |
||
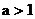 |
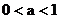 |
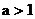 |
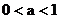 |
|
向x、y轴正负方向无限延伸 |
函数的定义域为R |
||
|
图象关于原点和y轴不对称 |
非奇非偶函数 |
||
|
函数图象都在x轴上方 |
函数的值域为R+ |
||
|
函数图象都过定点(0,1) |
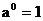 |
||
|
自左向右看, 图象逐渐上升 |
自左向右看, 图象逐渐下降 |
增函数 |
减函数 |
|
在第一象限内的图象纵坐标都大于1 |
在第一象限内的图象纵坐标都小于1 |
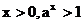 |
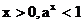 |
|
在第二象限内的图象纵坐标都小于1 |
在第二象限内的图象纵坐标都大于1 |
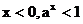 |
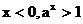 |
|
图象上升趋势是越来越陡 |
图象上升趋势是越来越缓 |
函数值开始增长较慢,到了某一值后增长速度极快; |
函数值开始减小极快,到了某一值后减小速度较慢; |
5.
利用函数的单调性,结合图象还可以看出:
(1)在[a,b]上,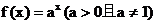 值域是
值域是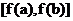 或
或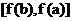 ;
(2)若
;
(2)若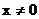 ,则
,则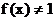 ;
;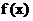 取遍所有正数当且仅当
取遍所有正数当且仅当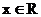 ;
(3)对于指数函数
;
(3)对于指数函数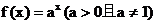 ,总有
,总有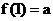 ;
(4)当
;
(4)当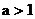 时,若
时,若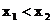 ,则
,则 ;
;
(一)指数函数的概念
一般地,函数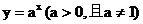 叫做指数函数(exponential
function),其中x是自变量,函数的定义域为R.
叫做指数函数(exponential
function),其中x是自变量,函数的定义域为R.
注意:1 指数函数的定义是一个形式定义,要引导学生辨析;
2 注意指数函数的底数的取值范围,引导学生分析底数为什么不能是负数、零和1.
巩固练习:利用指数函数的定义解决(教材P68例2、3)
4. 上面的几个函数有什么共同特征?
3. 一种放射性物质不断变化成其他物质,每经过一年的残留量是原来的84%,那么以时间x年为自变量,残留量y的函数关系式是什么?
2. 上一节中GDP问题中时间x与GDP值y的对应关系y=1.073x(x∈N*,x≤20)能否构成函数?
(备选引例)
1. (合作讨论)人口问题是全球性问题,由于全球人口迅猛增加,已引起全世界关注.世界人口2000年大约是60亿,而且以每年1.3%的增长率增长,按照这种增长速度,到2050年世界人口将达到100多亿,大有“人口爆炸”的趋势.为此,全球范围内敲起了人口警钟,并把每年的7月11日定为“世界人口日”,呼吁各国要控制人口增长.为了控制人口过快增长,许多国家都实行了计划生育.
我国人口问题更为突出,在耕地面积只占世界7%的国土上,却养育着22%的世界人口.因此,中国的人口问题是公认的社会问题.2000年第五次人口普查,中国人口已达到13亿,年增长率约为1%.为了有效地控制人口过快增长,实行计划生育成为我国一项基本国策.
1 按照上述材料中的1%的增长率,从2000年起,x年后我国的人口将达到2000年的多少倍?
2 到2050年我国的人口将达到多少?
3 你认为人口的过快增长会给社会的发展带来什么样的影响?
2. 选做题:教材P70习题2.1(B组) 第2题.
1. 必做题:教材P69习题2.1(A组) 第1-4题.
本节主要学习了根式与分数指数幂以及指数幂的运算,分数指数幂是根式的另一种表示形式,根式与分数指数幂可以进行互化.在进行指数幂的运算时,一般地,化指数为正指数,化根式为分数指数幂,化小数为分数进行运算,便于进行乘除、乘方、开方运算,以达到化繁为简的目的,对含有指数式或根式的乘除运算,还要善于利用幂的运算法则.
(一)指数与指数幂的运算
1.根式的概念
一般地,如果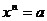 ,那么
,那么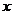 叫做
叫做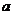 的
的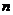 次方根(n th root),其中
次方根(n th root),其中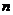 >1,且
>1,且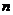 ∈
∈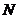 *.
*.
当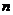 是奇数时,正数的
是奇数时,正数的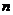 次方根是一个正数,负数的
次方根是一个正数,负数的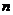 次方根是一个负数.此时,
次方根是一个负数.此时,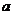 的
的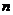 次方根用符号
次方根用符号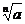 表示.
表示.
式子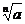 叫做根式(radical),这里
叫做根式(radical),这里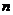 叫做根指数(radical
exponent),
叫做根指数(radical
exponent),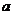 叫做被开方数(radicand).
叫做被开方数(radicand).
当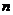 是偶数时,正数的
是偶数时,正数的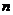 次方根有两个,这两个数互为相反数.此时,正数
次方根有两个,这两个数互为相反数.此时,正数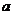 的正的
的正的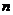 次方根用符号
次方根用符号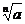 表示,负的
表示,负的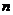 次方根用符号-
次方根用符号-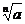 表示.正的
表示.正的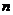 次方根与负的
次方根与负的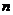 次方根可以合并成±
次方根可以合并成±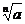 (
(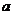 >0).
>0).
由此可得:负数没有偶次方根;0的任何次方根都是0,记作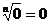 .
.
思考:(课本P58探究问题)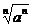 =
=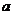 一定成立吗?.(学生活动)
一定成立吗?.(学生活动)
结论:当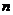 是奇数时,
是奇数时,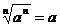
当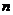 是偶数时,
是偶数时,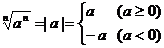
例1.(教材P58例1).
解:(略)
巩固练习:(教材P58例1)
2.分数指数幂
正数的分数指数幂的意义
规定:
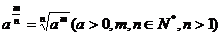
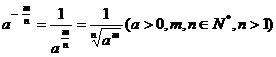
0的正分数指数幂等于0,0的负分数指数幂没有意义
指出:规定了分数指数幂的意义后,指数的概念就从整数指数推广到了有理数指数,那么整数指数幂的运算性质也同样可以推广到有理数指数幂.
3.有理指数幂的运算性质
(1)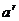 ·
·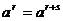
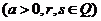 ;
;
(2)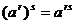
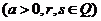 ;
;
(3)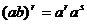
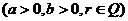 .
.
引导学生解决本课开头实例问题
例2.(教材P60例2、例3、例4、例5)
说明:让学生熟练掌握根式与分数指数幂的互化和有理指数幂的运算性质运用.
巩固练习:(教材P63练习1-3)
4. 无理指数幂
结合教材P62实例利用逼近的思想理解无理指数幂的意义.
指出:一般地,无理数指数幂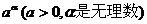 是一个确定的实数.有理数指数幂的运算性质同样适用于无理数指数幂.
是一个确定的实数.有理数指数幂的运算性质同样适用于无理数指数幂.
思考:(教材P63练习4)
巩固练习思考::(教材P62思考题)
例3.(新题讲解)从盛满1升纯酒精的容器中倒出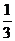 升,然后用水填满,再倒出
升,然后用水填满,再倒出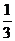 升,又用水填满,这样进行5次,则容器中剩下的纯酒精的升数为多少?
升,又用水填满,这样进行5次,则容器中剩下的纯酒精的升数为多少?
解:(略)
点评:本题还可以进一步推广,说明可以用指数的运算来解决生活中的实际问题.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com