
6.(2009北京文)设集合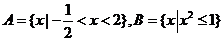 ,则
,则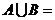 ( )
( )
A.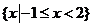 B.
B.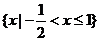
C.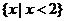 D.
D.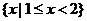
答案 A
解析 本题主要考查集合的基本运算以及简单的不等式的解法. 属于基础知识、基本运
算的考查∵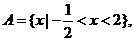
 ,
,
∴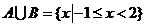 ,故选A.
,故选A.
5.(2009浙江文)设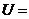
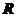 ,
,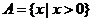 ,
,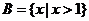 ,则
,则 ( ) A.
( ) A.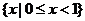 B.
B.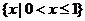 C.
C.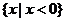 D.
D.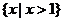
答案 B
[命题意图]本小题主要考查了集合中的补集、交集的知识,在集合的运算考查对于集合理解和掌握的程度,当然也很好地考查了不等式的基本性质.
解析 对于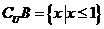 ,因此
,因此
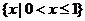 .
.
4.(2009浙江理)设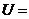
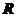 ,
,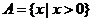 ,
,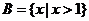 ,则
,则 ( )
( )
A.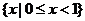 B.
B.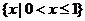 C.
C.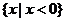 D.
D.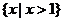
答案 B
解析 对于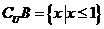 ,因此
,因此
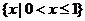 .
.
3.(2009浙江理)设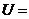
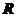 ,
,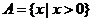 ,
,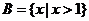 ,则
,则 ( )
( )
A.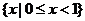 B.
B.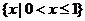 C.
C.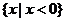 D.
D.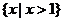
答案 B
解析 对于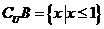 ,因此
,因此
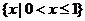
2.(2009全国卷Ⅰ理)设集合A={4,5,7,9},B={3,4,7,8,9},全集U=A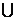 B,则
B,则
集合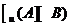 中的元素共有 ( )
中的元素共有 ( )
A.
3个 B. 4个 C. 5个
D. 6个 
解: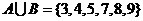 ,
,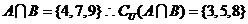 故选A。也可用摩根律:
故选A。也可用摩根律: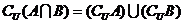
答案 A
1.(2009年广东卷文)已知全集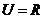 ,则正确表示集合
,则正确表示集合 和
和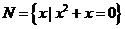 关系的韦恩(Venn)图是 ( )
关系的韦恩(Venn)图是 ( )
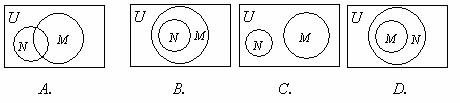
答案 B
解析 由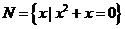 ,得
,得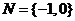 ,则
,则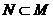 ,选B.
,选B.
2009年高考题
14、方程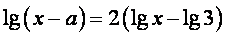 至少有一个实数根的充要条件是
至少有一个实数根的充要条件是
15,设数列{an}中a1=2,an+1=an+n+1,则通项an= .
三,解答题:本大题共6小题,共75分,解答应写出文字说明,证明过程或演算步骤
16(本小题满分12分)已知△ABC的三个内角A、B、C的对边分别是a、b、c,
若向量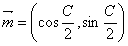 与
与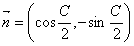 的夹角为
的夹角为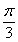 .
.
(1)求角C;(2)若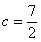 ,△ABC的面积为
,△ABC的面积为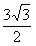 ,求
,求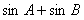 的值.
的值.
17(本小题满分12分)设定义域为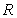 的奇函数
的奇函数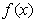 是减函数,若当
是减函数,若当 时,
时,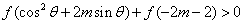 恒成立,求实数
恒成立,求实数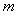 的取值范围.
的取值范围.
18(本小题满分12分)设函数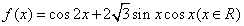 的最大值为
的最大值为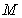 ,最小正周
,最小正周
期为 .
.
(Ⅰ)求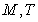 的值及单调递增区间;
的值及单调递增区间;
(Ⅱ)10个互不相等的正数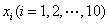 满足
满足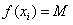 ,且
,且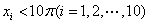 ,
,
求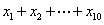 的值.
的值.
19(本小题满分12分) 已知函数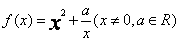
(1)当  时,解不等式:
时,解不等式: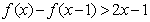
(2)讨论函数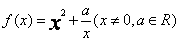 的奇偶性,并说明理由
的奇偶性,并说明理由
20(本小题满分13分) 已知函数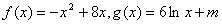
(Ⅰ)求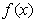 在区间
在区间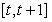 上的最大值
上的最大值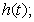
(Ⅱ)是否存在实数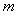 ,使得
,使得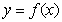 的图象与
的图象与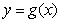 的图象有且只有三个交点?若存在,若存在,求出
的图象有且只有三个交点?若存在,若存在,求出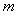 的取值范围,若不存在,说明理由.
的取值范围,若不存在,说明理由.
21(本小题满分14分)
在数列{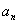 }中,已知
}中,已知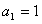 ,
,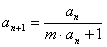 (
(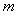 是常数,
是常数,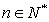 ),
),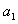 ,
,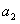 ,
,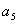 成公比不等于1的等比数列.(1)求证:数列
成公比不等于1的等比数列.(1)求证:数列 是等差数列;(2)求数列{
是等差数列;(2)求数列{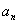 }的通项公式;
}的通项公式;
(3)设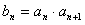 ,数列{
,数列{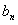 }的前
}的前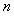 项和为
项和为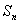 ,求证:
,求证: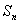 <
<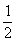 .
.
10.边长为5、7、8的三角形的最大角与最小角之和为 ( )
A. 90° B. 120° C. 135° D.150°
第Ⅱ卷(非选择题 共100分)
二,填空题:本大题共5小题,每小题5分,共25分,把答案填在题中横线上.
11,若曲线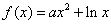 存在垂直于
存在垂直于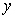 轴的切线,则实数
轴的切线,则实数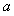 的取值范围是
的取值范围是
12,设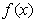 是定义域为
是定义域为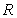 的奇函数,且在
的奇函数,且在 上是减函数,若
上是减函数,若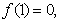 则不等式
则不等式
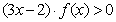 的解集是
的解集是
13,在 中,已知
中,已知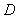 是
是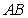 边上的一点,若
边上的一点,若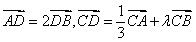 ,
,
则实数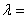
5.已知下列命题中:
(1)若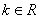 ,且
,且 ,则
,则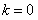 或
或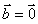 ,
,
(2)若 ,则
,则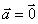 或
或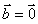

(3)若不平行的两个非零向量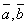 ,满足
,满足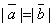 ,则
,则

(4)若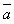 与
与 平行,则
平行,则 ,其中真命题的个数是 ( )
,其中真命题的个数是 ( )
A.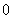 B.
B.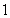 C.
C. D.
D.

6,在 中,
中,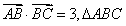 的面积
的面积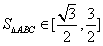 ,则
,则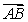 与
与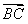 夹角的取值范围是 ( )
夹角的取值范围是 ( )
A, 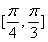 B,
B, 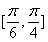 C,
C, 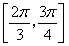 D,
D, 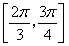

7,已知函数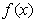 满足:当
满足:当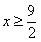 时,
时, ,当
,当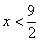 时,
时,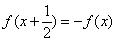 ,则
,则
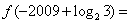 ( )
( )
A, 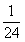 B,
B, 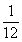 C,
C, 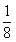 D,
D, 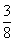

8,设函数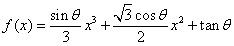 ,其中
,其中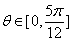 ,
,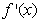 为
为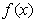 的导函数,则
的导函数,则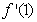 的取值范围是
( )
的取值范围是
( )
A, 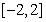 B,
B, 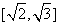 C,
C, 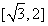 D,
D, 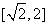
9,已知直线y=x+a与曲线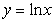 相切,则实数
相切,则实数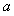 的值是 ( )
的值是 ( )
A, 1
B, 2
C, 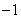 D,
D,
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com