
2009年高考题
9.(2008年四川省成都市一诊)已知函数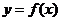 是定义域为R的偶函数,其图像均在x轴
是定义域为R的偶函数,其图像均在x轴
的上方,对任意的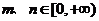 ,都有
,都有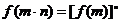 ,且
,且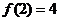 ,又当
,又当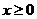 时,其导函数
时,其导函数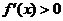 恒成立。
恒成立。
(Ⅰ)求f(0)、f(-1)的值;
(Ⅱ)解关于x的不等式: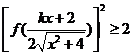 ,其中
,其中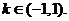
解 (1)由f(m·n)=[f(m)]n得:f(0)=f(0×0)=[f(0)]0
∵函数f(x)的图象均在x轴的上方,∴f(0)>0,∴f(0)=1 ……………………………3分
∵f(2)=f(1×2)=[f(1)]2=4,又f(x)>0∴f(1)=2,f(-1)=f(1)=2 …………………3分
(2)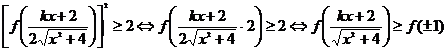
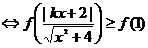
又当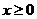 时,其导函数
时,其导函数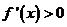 恒成立,∴
恒成立,∴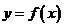 在区间
在区间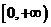 上为单调递增函数
上为单调递增函数
∴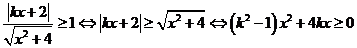
①当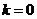 时,
时,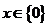 ;
;
②当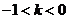 时,
时,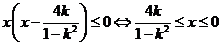 ,∴
,∴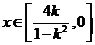 ;
;
③当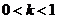 时,
时,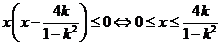 ,∴
,∴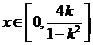
综上所述:当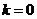 时,
时,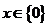 ;当
;当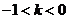 时,
时,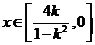 ;
;
当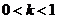 时,
时,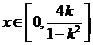 。
。
8.(2007年江苏省淮安市)已知函数F(x)=|2x-t|-x3+x+1(x∈R,t为常数,t∈R)
(1)写出此函数F(x)在R上的单调区间;
(2)若方程F(x)-m=0恰有两解,求实数m的值。
解 (1)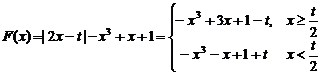 ∴
∴
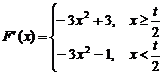
由-3x2+3=0 得x1=-1,x2=1,而-3x2-1<0恒成立
∴ i) 当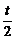 <-1时,F(x)在区间(-∞,-1)上是减函数
<-1时,F(x)在区间(-∞,-1)上是减函数
在区间(-1,1)上是增函数,在区间(1,+∞)上是减函数
ii) 当1>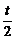 ≥-1时,F(x)在区间(-∞,
≥-1时,F(x)在区间(-∞,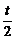 )上是减函数
)上是减函数
在区间(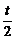 ,1)上是增函数,在区间(1,+∞)上是减函数
,1)上是增函数,在区间(1,+∞)上是减函数
iii) 当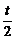 ≥1时,F(x)在(-∞,+∞)上是减函数
≥1时,F(x)在(-∞,+∞)上是减函数
(2)由(1)可知
i) 当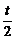 <-1时,F(x)在x=-1处取得极小值-1-t,
<-1时,F(x)在x=-1处取得极小值-1-t,
在x=1处取得极大值3-t,若方程F(x)-m=0恰有两解,
此时m=-1-t或m=3-t
ii) 当-1≤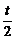 <1,F(x)在x=
<1,F(x)在x=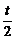 处取值为
处取值为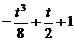 ,
,
在x=1处取得极大值3-t,若方程F(x)-m=0恰有两解,
此时m=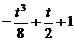 或m=3-t
或m=3-t
8.(北京市十一学校2008届高三数学练习题)如图为函数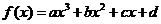 的图象,
的图象,
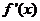 为函数
为函数 的导函数,则不等式
的导函数,则不等式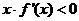 的解集为______ ______.
的解集为______ ______.
答案 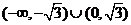
7.(四川省成都市新都一中高2008级12月月考)已知函数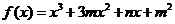 在
在
x=-1时有极值0,则m=_________;n=_________;
本题主要考查函数、导数、极值等基本概念和性质0
答案 m=2,n=9.
 解析
解析 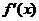 =3x2+6mx+n
由题意,
=3x2+6mx+n
由题意,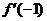 =3-6m+n=0
f(-1)=-1+3m-n+m2=0
解得
=3-6m+n=0
f(-1)=-1+3m-n+m2=0
解得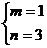 或
或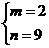 但m=1,n=3时,
但m=1,n=3时,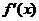 =3x2+6x+3=3(x+1)2≥0恒成立
即x=-1时不是f(x)的极值点,应舍去
=3x2+6x+3=3(x+1)2≥0恒成立
即x=-1时不是f(x)的极值点,应舍去
6.(2008年高考数学各校月考)定积分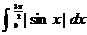 的值是
.
的值是
.
答案 3
5.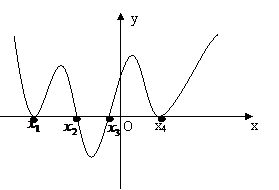 (湖南省株洲市2008届高三第二次质检)已知函数
(湖南省株洲市2008届高三第二次质检)已知函数 的导函数
的导函数 的图像如下,则 ( )
的图像如下,则 ( )
A.函数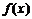 有1个极大值点,1个极小值点
有1个极大值点,1个极小值点
B.函数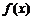 有2个极大值点,2个极小值点
有2个极大值点,2个极小值点
C.函数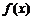 有3个极大值点,1个极小值点
有3个极大值点,1个极小值点
D.函数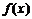 有1个极大值点,3个极小值点
有1个极大值点,3个极小值点
答案 A
4.(江西省五校2008届高三开学联考)已知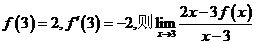 ( )
( )
A.-4 B.8 C.0 D.不存在
答案 B
3.(江西省五校2008届高三开学联考)设函数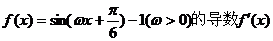
的最大值为3,则f(x)的图象的一条对称轴的方程是 ( )
A.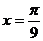 B.
B.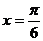
C.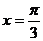 D.
D.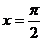
答案 C
2.(安徽省皖南八校2008届高三第一次联考)若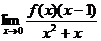 存在,则
存在,则 不可
不可
能为 ( )
A.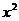 ; B.
; B.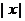 ; C.
; C.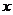 ; D.
; D.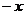 ;
;
答案 B
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com