
42.(2009湖北卷文)(本小题满分14分)
已知关于x的函数f(x)=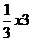 +bx2+cx+bc,其导函数为f+(x).令g(x)=∣f+(x) ∣,
+bx2+cx+bc,其导函数为f+(x).令g(x)=∣f+(x) ∣,
记函数g(x)在区间[-1、1]上的最大值为M.
(Ⅰ)如果函数f(x)在x=1处有极值-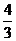 ,试确定b、c的值:
,试确定b、c的值:
(Ⅱ)若∣b∣>1,证明对任意的c,都有M>2:
(Ⅲ)若M≧K对任意的b、c恒成立,试求k的最大值。
本小题主要考察函数、函数的导数和不等式等基础知识,考察综合运用数学知识进行推理
论证的能力和份额类讨论的思想(满分14分)
(I)解析 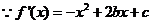 ,由
,由 在
在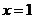 处有极值
处有极值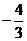
可得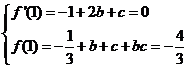
解得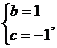 或
或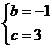
若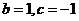 ,则
,则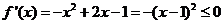 ,此时
,此时 没有极值;
没有极值;
若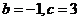 ,则
,则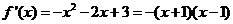
当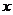 变化时,
变化时, ,
,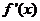 的变化情况如下表:
的变化情况如下表:
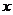 |
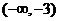 |
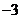 |
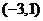 |
1 |
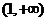 |
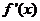 |
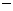 |
0 |
+ |
0 |
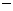 |
 |
 |
极小值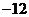 |
 |
极大值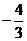 |
 |
 当
当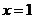 时,
时, 有极大值
有极大值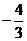 ,故
,故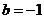 ,
,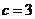 即为所求。
即为所求。
(Ⅱ)证法1: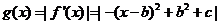
当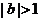 时,函数
时,函数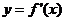 的对称轴
的对称轴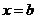 位于区间
位于区间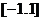 之外。
之外。
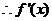 在
在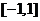 上的最值在两端点处取得
上的最值在两端点处取得
故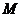 应是
应是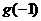 和
和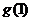 中较大的一个
中较大的一个
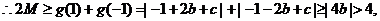 即
即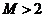
证法2(反证法):因为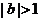 ,所以函数
,所以函数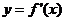 的对称轴
的对称轴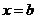 位于区间
位于区间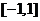 之外,
之外,
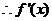 在
在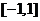 上的最值在两端点处取得。
上的最值在两端点处取得。
故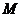 应是
应是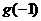 和
和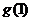 中较大的一个
中较大的一个
假设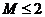 ,则
,则
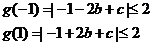


将上述两式相加得:
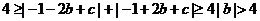 ,导致矛盾,
,导致矛盾,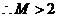
(Ⅲ)解法1: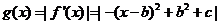
(1)当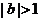 时,由(Ⅱ)可知
时,由(Ⅱ)可知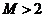 ;
;
(2)当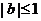 时,函数
时,函数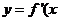 )的对称轴
)的对称轴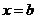 位于区间
位于区间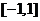 内,
内,
此时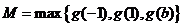
由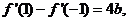 有
有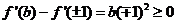
①若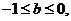 则
则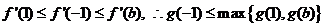 ,
,
于是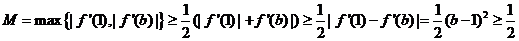
②若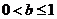 ,则
,则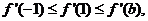
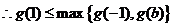
于是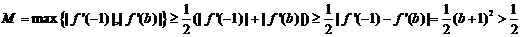
综上,对任意的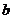 、
、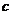 都有
都有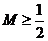
而当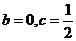 时,
时,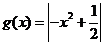 在区间
在区间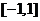 上的最大值
上的最大值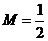
故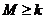 对任意的
对任意的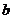 、
、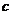 恒成立的
恒成立的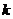 的最大值为
的最大值为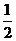 。
。
解法2: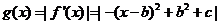
(1)当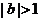 时,由(Ⅱ)可知
时,由(Ⅱ)可知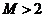 ;
;
(2)当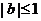 时,函数
时,函数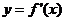 的对称轴
的对称轴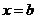 位于区间
位于区间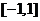 内,
内,
此时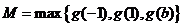
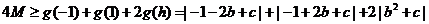
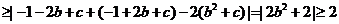 ,即
,即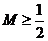
下同解法1
41.(2009四川卷文)(本小题满分12分)
已知函数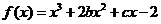 的图象在与
的图象在与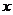 轴交点处的切线方程是
轴交点处的切线方程是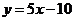 。
。
(I)求函数 的解析式;
的解析式;
(II)设函数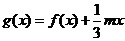 ,若
,若 的极值存在,求实数
的极值存在,求实数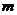 的取值范围以及函数
的取值范围以及函数 取得极值时对应的自变量
取得极值时对应的自变量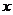 的值.
的值.
解析 (I)由已知,切点为(2,0),故有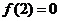 ,即
,即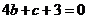 ……①
……①
又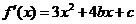 ,由已知
,由已知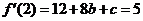 得
得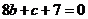 ……②
……②
联立①②,解得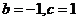 .
.
所以函数的解析式为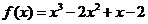 …………………………………4分
…………………………………4分
(II)因为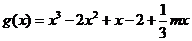


令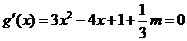
当函数有极值时,则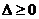 ,方程
,方程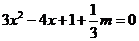 有实数解,
有实数解,
由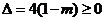 ,得
,得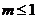 .
.
①当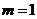 时,
时,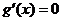 有实数
有实数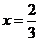 ,在
,在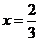 左右两侧均有
左右两侧均有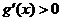 ,故函数
,故函数 无极值
无极值
②当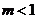 时,
时,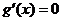 有两个实数根
有两个实数根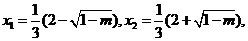
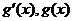 情况如下表:
情况如下表:
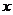 |
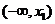 |
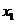 |
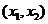 |
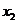 |
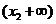 |
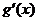 |
+ |
0 |
- |
0 |
+ |
 |
↗ |
极大值 |
↘ |
极小值 |
↗ |
所以在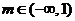 时,函数
时,函数 有极值;
有极值;
当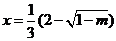 时,
时, 有极大值;当
有极大值;当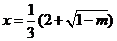 时,
时, 有极小值;
有极小值;
…………………………………12分
40.(2009陕西卷理)(本小题满分12分)
已知函数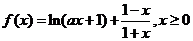 ,其中
,其中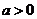
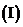 若
若 在x=1处取得极值,求a的值;
在x=1处取得极值,求a的值; 

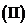 求
求 的单调区间;
的单调区间;
(Ⅲ)若 的最小值为1,求a的取值范围。
的最小值为1,求a的取值范围。
解(Ⅰ)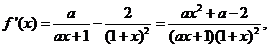
∵ 在x=1处取得极值,∴
在x=1处取得极值,∴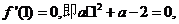 解得
解得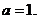
(Ⅱ)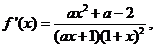
∵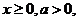 ∴
∴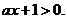
①当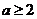 时,在区间
时,在区间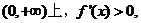 ∴
∴ 的单调增区间为
的单调增区间为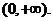
②当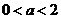 时,
时,
由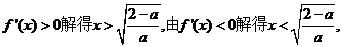
∴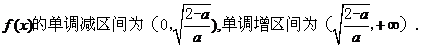
(Ⅲ)当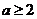 时,由(Ⅱ)①知,
时,由(Ⅱ)①知,
当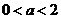 时,由(Ⅱ)②知,
时,由(Ⅱ)②知, 在
在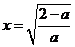 处取得最小值
处取得最小值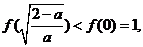
综上可知,若 得最小值为1,则a的取值范围是
得最小值为1,则a的取值范围是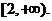
39.(2009陕西卷文)(本小题满分12分)
已知函数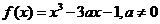
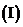 求
求 的单调区间;
的单调区间;
 若
若 在
在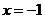 处取得极值,直线y=my与
处取得极值,直线y=my与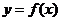 的图象有三个不同的交点,求m的取值范围。
的图象有三个不同的交点,求m的取值范围。
解析 (1)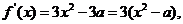
当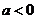 时,对
时,对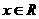 ,有
,有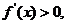
当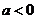 时,
时, 的单调增区间为
的单调增区间为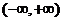
当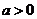 时,由
时,由 解得
解得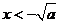 或
或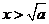 ;
;
由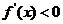 解得
解得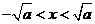 ,
,
当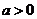 时,
时, 的单调增区间为
的单调增区间为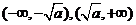 ;
; 的单调减区间为
的单调减区间为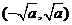 。
。
(2)因为 在
在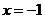 处取得极大值,
处取得极大值,
所以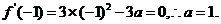
所以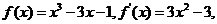
由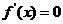 解得
解得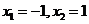 。
。
由(1)中 的单调性可知,
的单调性可知, 在
在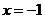 处取得极大值
处取得极大值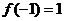 ,
,
在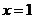 处取得极小值
处取得极小值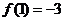 。
。
因为直线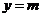 与函数
与函数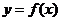 的图象有三个不同的交点,又
的图象有三个不同的交点,又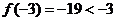 ,
,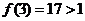 ,
,
结合 的单调性可知,
的单调性可知, 的取值范围是
的取值范围是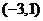 。
。
38.(2009宁夏海南卷理)(本小题满分12分)
已知函数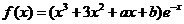
(1)如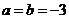 ,求
,求 的单调区间;
的单调区间;
(1)若 在
在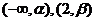 单调增加,在
单调增加,在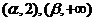 单调减少,证明
单调减少,证明
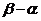 <6.
<6.
(21)解析
(Ⅰ)当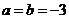 时,
时,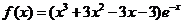 ,故
,故
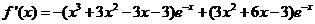
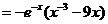
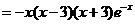
当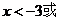
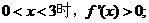
当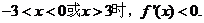
从而 单调减少.
单调减少.
(Ⅱ)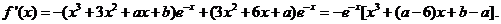
由条件得: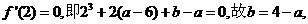 从而
从而
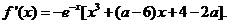
因为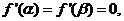 所以
所以
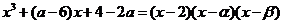
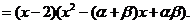
将右边展开,与左边比较系数得,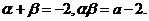 故
故
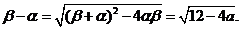
又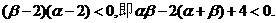 由此可得
由此可得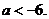


于是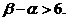
37.(2009辽宁卷理)(本小题满分12分)
已知函数f(x)=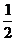 x
x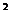 -ax+(a-1)
-ax+(a-1)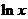 ,
,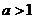 。
。
(1)讨论函数 的单调性;
的单调性;
(2)证明:若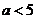 ,则对任意x
,则对任意x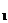 ,x
,x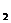
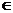
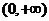 ,x
,x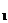
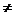 x
x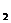 ,有
,有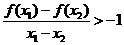 。
。
解析 (1) 的定义域为
的定义域为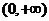 。
。
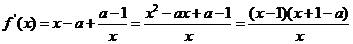 2分
2分
(i)若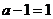 即
即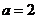 ,则
,则
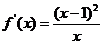
故 在
在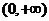 单调增加。
单调增加。
(ii)若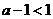 ,而
,而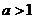 ,故
,故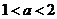 ,则当
,则当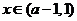 时,
时,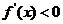 ;
;
当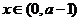 及
及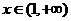 时,
时,
故 在
在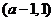 单调减少,在
单调减少,在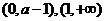 单调增加。
单调增加。
(iii)若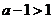 ,即
,即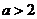 ,同理可得
,同理可得 在
在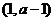 单调减少,在
单调减少,在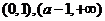 单调增加.
单调增加.
(II)考虑函数 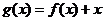
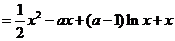
则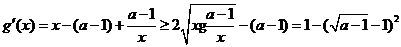
由于1<a<5,故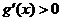 ,即g(x)在(4, +∞)单调增加,从而当
,即g(x)在(4, +∞)单调增加,从而当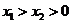 时有
时有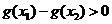 ,即
,即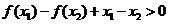 ,故
,故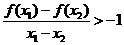 ,当
,当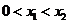 时,有
时,有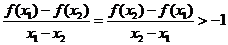 ·········12分
·········12分
36.(2009辽宁卷文)(本小题满分12分)
设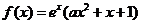 ,且曲线y=f(x)在x=1处的切线与x轴平行。
,且曲线y=f(x)在x=1处的切线与x轴平行。
(2)求a的值,并讨论f(x)的单调性;
(1)证明:当
解析 (Ⅰ)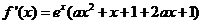 .有条件知,
.有条件知,
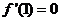 ,故
,故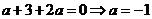 .
………2分 于是
.
………2分 于是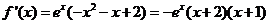 .
.
故当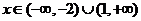 时,
时,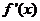 <0;
<0;
当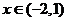 时,
时,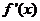 >0.
>0.
从而 在
在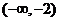 ,
,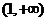 单调减少,在
单调减少,在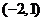 单调增加. ………6分
单调增加. ………6分
(Ⅱ)由(Ⅰ)知 在
在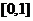 单调增加,故
单调增加,故 在
在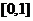 的最大值为
的最大值为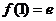 ,
,
最小值为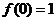 .
.
从而对任意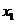 ,
,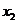
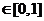 ,有
,有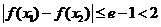 .
………10分
.
………10分
而当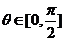 时,
时,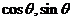
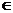
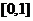 .
.
从而 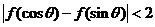 ………12分
………12分
35.(2009福建卷理)(本小题满分14分)
已知函数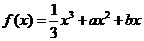 ,且
,且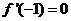
(1) 试用含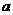 的代数式表示b,并求
的代数式表示b,并求 的单调区间;
的单调区间;
(2)令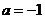 ,设函数
,设函数 在
在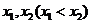 处取得极值,记点M (
处取得极值,记点M (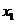 ,
,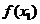 ),N(
),N(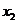 ,
,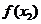 ),P(
),P(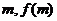 ),
), 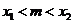 ,请仔细观察曲线
,请仔细观察曲线 在点P处的切线与线段MP的位置变化趋势,并解释以下问题:
在点P处的切线与线段MP的位置变化趋势,并解释以下问题:
(I)若对任意的m 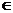 (
(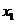 ,
x
,
x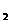 ),线段MP与曲线f(x)均有异于M,P的公共点,试确定t的最小值,并证明你的结论;
),线段MP与曲线f(x)均有异于M,P的公共点,试确定t的最小值,并证明你的结论;
(II)若存在点Q(n ,f(n)), x 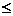 n<
m,使得线段PQ与曲线f(x)有异于P、Q的公共点,请直接写出m的取值范围(不必给出求解过程)
n<
m,使得线段PQ与曲线f(x)有异于P、Q的公共点,请直接写出m的取值范围(不必给出求解过程)
解法一:
(Ⅰ)依题意,得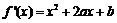
由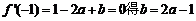 .
.
从而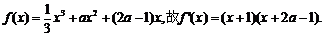
令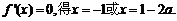


①当a>1时,
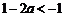
当x变化时,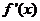 与
与 的变化情况如下表:
的变化情况如下表:
|
x |
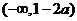 |
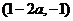 |
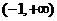 |
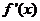 |
+ |
- |
+ |
 |
单调递增 |
单调递减 |
单调递增 |
由此得,函数 的单调增区间为
的单调增区间为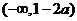 和
和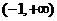 ,单调减区间为
,单调减区间为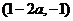 。
。
②当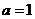 时,
时,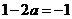 此时有
此时有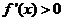 恒成立,且仅在
恒成立,且仅在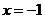 处
处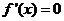 ,故函数
,故函数 的单调增区间为R
的单调增区间为R
③当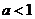 时,
时,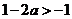 同理可得,函数
同理可得,函数 的单调增区间为
的单调增区间为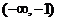 和
和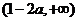 ,单调减区间为
,单调减区间为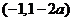


综上:
当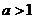 时,函数
时,函数 的单调增区间为
的单调增区间为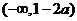 和
和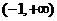 ,单调减区间为
,单调减区间为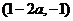 ;
;
当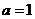 时,函数
时,函数 的单调增区间为R;
的单调增区间为R;
当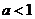 时,函数
时,函数 的单调增区间为
的单调增区间为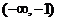 和
和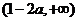 ,单调减区间为
,单调减区间为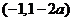 .
.
(Ⅱ)由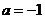 得
得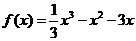 令
令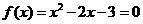 得
得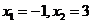
由(1)得 增区间为
增区间为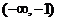 和
和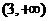 ,单调减区间为
,单调减区间为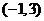 ,所以函数
,所以函数 在处
在处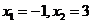 取得极值,故M(
取得极值,故M(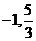 )N(
)N(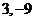 )。
)。
观察 的图象,有如下现象:
的图象,有如下现象:
①当m从-1(不含-1)变化到3时,线段MP的斜率与曲线 在点P处切线的斜率
在点P处切线的斜率 之差Kmp-
之差Kmp-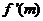 的值由正连续变为负。
的值由正连续变为负。
②线段MP与曲线是否有异于H,P的公共点与Kmp-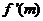 的m正负有着密切的关联;
的m正负有着密切的关联;
③Kmp-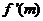 =0对应的位置可能是临界点,故推测:满足Kmp-
=0对应的位置可能是临界点,故推测:满足Kmp-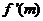 的m就是所求的t最小值,下面给出证明并确定的t最小值.曲线
的m就是所求的t最小值,下面给出证明并确定的t最小值.曲线 在点
在点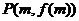 处的切线斜率
处的切线斜率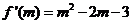 ;
;
线段MP的斜率Kmp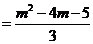
当Kmp-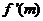 =0时,解得
=0时,解得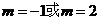
直线MP的方程为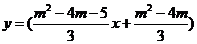


令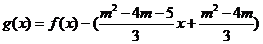
当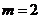 时,
时,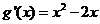 在
在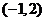 上只有一个零点
上只有一个零点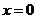 ,可判断
,可判断 函数在
函数在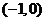 上单调递增,在
上单调递增,在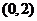 上单调递减,又
上单调递减,又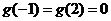 ,所以
,所以 在
在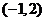 上没有零点,即线段MP与曲线
上没有零点,即线段MP与曲线 没有异于M,P的公共点。
没有异于M,P的公共点。
当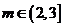 时,
时,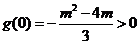 .
.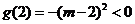
所以存在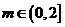 使得
使得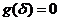
即当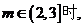 MP与曲线
MP与曲线 有异于M,P的公共点
有异于M,P的公共点


综上,t的最小值为2.
(2)类似(1)于中的观察,可得m的取值范围为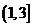
解法二:
(1)同解法一.
(2)由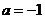 得
得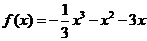 ,令
,令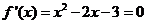 ,得
,得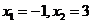
由(1)得的 单调增区间为
单调增区间为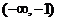 和
和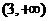 ,单调减区间为
,单调减区间为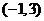 ,所以函数在处取得极值。故M(
,所以函数在处取得极值。故M(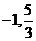 ).N(
).N(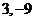 )
)
(Ⅰ)
直线MP的方程为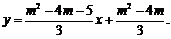
由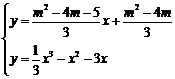
得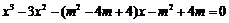
线段MP与曲线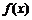 有异于M,P的公共点等价于上述方程在(-1,m)上有根,即函数
有异于M,P的公共点等价于上述方程在(-1,m)上有根,即函数
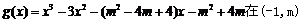 上有零点.
上有零点.
因为函数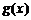 为三次函数,所以
为三次函数,所以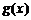 至多有三个零点,两个极值点.
至多有三个零点,两个极值点.
又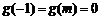 .因此,
.因此,
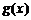 在
在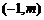 上有零点等价于
上有零点等价于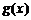 在
在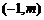 内恰有一个极大值点和一个极小值点,即
内恰有一个极大值点和一个极小值点,即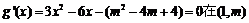 内有两不相等的实数根.
内有两不相等的实数根.
等价于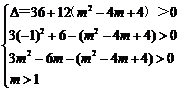 即
即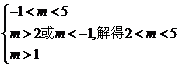
又因为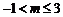 ,所以m
的取值范围为(2,3)
,所以m
的取值范围为(2,3)
从而满足题设条件的r的最小值为2.
333.(2009湖南卷文)(本小题满分13分)
已知函数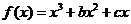 的导函数的图象关于直线x=2对称.
的导函数的图象关于直线x=2对称.
(Ⅰ)求b的值;
(Ⅱ)若 在
在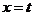 处取得最小值,记此极小值为
处取得最小值,记此极小值为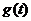 ,求
,求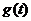 的定义域和值域。
的定义域和值域。
解: (Ⅰ)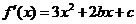 .因为函数
.因为函数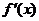 的图象关于直线x=2对称,
的图象关于直线x=2对称,
所以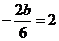 ,于是
,于是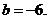
(Ⅱ)由(Ⅰ)知,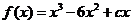 ,
,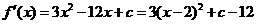 .
.
(ⅰ)当c 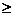 12时,
12时,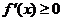 ,此时
,此时 无极值。
无极值。
(ii)当c<12时,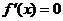 有两个互异实根
有两个互异实根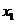 ,
,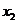 .不妨设
.不妨设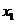 <
<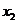 ,则
,则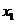 <2<
<2<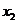 .
.
当x<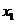 时,
时,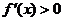 ,
,  在区间
在区间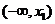 内为增函数;
内为增函数; 

当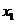 <x<
<x<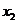 时,
时,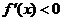 ,
, 在区间
在区间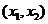 内为减函数;
内为减函数;
当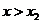 时,
时,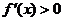 ,
, 在区间
在区间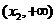 内为增函数.
内为增函数.
所以 在
在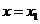 处取极大值,在
处取极大值,在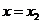 处取极小值.
处取极小值.
因此,当且仅当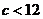 时,函数
时,函数 在
在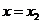 处存在唯一极小值,所以
处存在唯一极小值,所以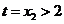 .
.
于是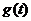 的定义域为
的定义域为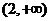 .由
.由 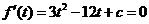 得
得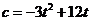 .
.
于是 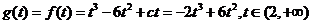 .
.
当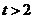 时,
时,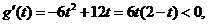 所以函数
所以函数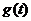
在区间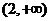 内是减函数,故
内是减函数,故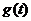 的值域为
的值域为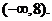


32.(2009全国卷Ⅱ理)(本小题满分12分)
设函数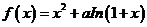 有两个极值点
有两个极值点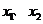 ,且
,且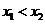
(I)求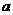 的取值范围,并讨论
的取值范围,并讨论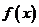 的单调性;
的单调性;
(II)证明: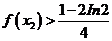
解: (I)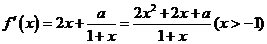
令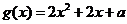 ,其对称轴为
,其对称轴为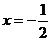 。由题意知
。由题意知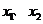 是方程
是方程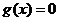 的两个均大于
的两个均大于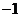 的不相等的实根,其充要条件为
的不相等的实根,其充要条件为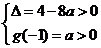 ,得
,得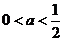
⑴当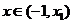 时,
时,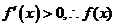 在
在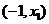 内为增函数;
内为增函数;


⑵当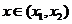 时,
时,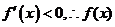 在
在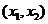 内为减函数;
内为减函数;
⑶当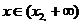 时,
时,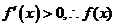 在
在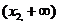 内为增函数;
内为增函数;
(II)由(I)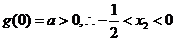 ,
,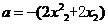
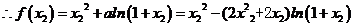
设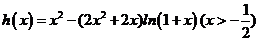 ,
,
则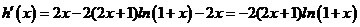
⑴当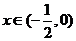 时,
时,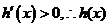 在
在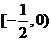 单调递增;
单调递增;
⑵当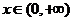 时,
时,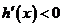 ,
,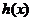 在
在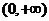 单调递减。
单调递减。


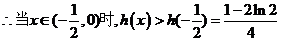
故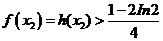 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com