
3.(福建省福州市普通高中09年高三质量检查)已知
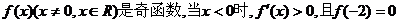 ,则不等式
,则不等式
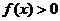 的解集是 ( )
的解集是 ( )
A.(-2,0) B.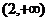
C.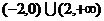 D.
D.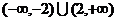
答案 C
2.若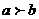 ,则(安徽省示范高中皖北协作区2009届高三第一次联考试题)下列
,则(安徽省示范高中皖北协作区2009届高三第一次联考试题)下列 不等式中正确的是 ( )
不等式中正确的是 ( )
A 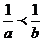 B
B
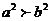 C
C 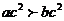 D
D 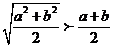
答案 D
1、(山东省乐陵一中2009届高三考前练习)已知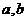 为非零实数,且
为非零实数,且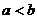 ,则下列命题成立的是 ( )
,则下列命题成立的是 ( )
A . 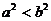 B.
B.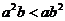 C.
C.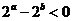 D.
D.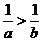
答案 C
2009年联考题
30.(2007湖北)已知m,n为正整数.
(Ⅰ)用数学归纳法证明:当x>-1时,(1+x)m≥1+mx;
(Ⅱ)对于n≥6,已知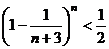 ,求证
,求证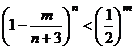 ,m=1,1,2…,n;
,m=1,1,2…,n;
(Ⅲ)求出满足等式3n+4m+…+(n+2)m=(n+3)n的所有正整数n.
解:(Ⅰ)证:当x=0或m=1时,原不等式中等号显然成立,下用数学归纳法证明:
当x>-1,且x≠0时,m≥2,(1+x)m>1+mx. 1
(i)当m=2时,左边=1+2x+x2,右边=1+2x,因为x≠0,所以x2>0,即左边>右边,不等式①成立;
(ii)假设当m=k(k≥2)时,不等式①成立,即(1+x)k>1+kx,则当m=k+1时,因为x>-1,所以1+x>0.又因为x≠0,k≥2,所以kx2>0.
于是在不等式(1+x)k>1+kx两边同乘以1+x得
(1+x)k·(1+x)>(1+kx)(1+x)=1+(k+1)x+kx2>1+(k+1)x,
所以(1+x)k+1>1+(k+1)x,即当m=k+1时,不等式①也成立.
综上所述,所证不等式成立.
(Ⅱ)证:当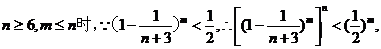
而由(Ⅰ),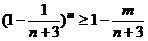
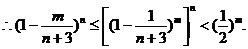
(Ⅲ)解:假设存在正整数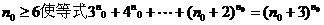 成立,
成立,
即有(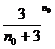 )+
)+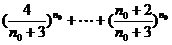 =1. ②
=1. ②
又由(Ⅱ)可得
(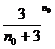 )+
)+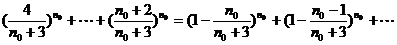
+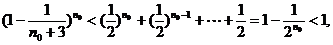 与②式矛盾,
与②式矛盾,
故当n≥6时,不存在满足该等式的正整数n.
故只需要讨论n=1,2,3,4,5的情形;
当n=1时,3≠4,等式不成立;
当n=2时,32+42=52,等式成立;
当n=3时,33+43+53=63,等式成立;
当n=4时,34+44+54+64为偶数,而74为奇数,故34+44+54+64≠74,等式不成立;
当n=5时,同n=4的情形可分析出,等式不成立.
综上,所求的n只有n=2,3.
29.(2007北京)记关于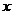 的不等式
的不等式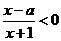 的解集为
的解集为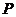 ,不等式
,不等式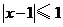 的解集为
的解集为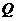 .
.
(I)若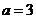 ,求
,求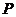 ;
;
(II)若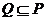 ,求正数
,求正数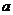 的取值范围.
的取值范围.
解:(I)由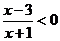 ,得
,得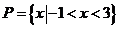 .
.
(II)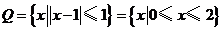 .
.
由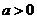 ,得
,得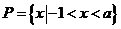 ,又
,又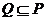 ,所以
,所以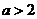 ,
,
即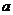 的取值范围是
的取值范围是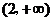 .
.
28.(2006上海)不等式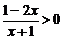 的解集是
.
的解集是
.
答案 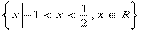 .
.
解析 应用结论: 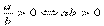 .不等式
.不等式
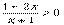 等价于(1-2x)(x+1)>0,也就是
等价于(1-2x)(x+1)>0,也就是 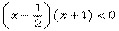 ,所以
,所以
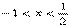 ,从而应填
,从而应填
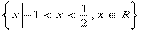 .
.
27.(2006浙江)不等式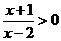 的解集是 。.
的解集是 。.
答案  x<-1或x>2
x<-1或x>2
解析 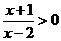 Û(x+1)(x-2)>0Ûx<-1或x>2.
Û(x+1)(x-2)>0Ûx<-1或x>2.
26.(2006江苏)不等式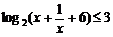 的解集为
的解集为
[思路点拨]本题考查对数函数单调性和不等式的解法
答案 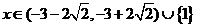
解析 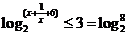 ,0〈
,0〈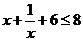 ,
,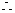
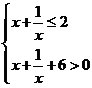 .
.
解得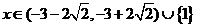
25.(2007北京)已知集合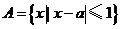 ,
,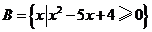 .若
.若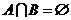 ,则实数
,则实数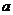 的取值范围是 (2,3) .
的取值范围是 (2,3) .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com