
16.(2009山东卷文)某公司租赁甲、乙两种设备生产A,B两类产品,甲种设备每天能生产A类产品5件和B类产品10件,乙种设备每天能生产A类产品6件和B类产品20件.已知设备甲每天的租赁费为200元,设备乙每天的租赁费为300元,现该公司至少要生产A类产品50件,B类产品140件,所需租赁费最少为__________元. 

答案 2300
解析 设甲种设备需要生产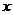 天, 乙种设备需要生产
天, 乙种设备需要生产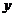 天, 该公司所需租赁费为
天, 该公司所需租赁费为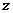 元,则
元,则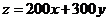 ,甲、乙两种设备生产A,B两类产品的情况为下表所示:
,甲、乙两种设备生产A,B两类产品的情况为下表所示:
 产品 产品
设备 |
A类产品 (件)(≥50) |
B类产品 (件)(≥140) |
租赁费 (元) |
|
甲设备 |
5
|
10 |
200 |
|
乙设备 |
6
|
20
|
300 |
则满足的关系为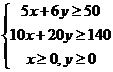 即:
即: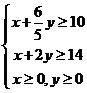 ,
, 

作出不等式表示的平面区域,当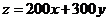 对应的直线过两直线
对应的直线过两直线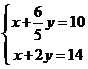 的交点(4,5)时,目标函数
的交点(4,5)时,目标函数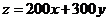 取得最低为2300元.
取得最低为2300元. 

[命题立意]:本题是线性规划的实际应用问题,需要通过审题理解题意,找出各量之间的关系,最好是列成表格,找出线性约束条件,写出所研究的目标函数,通过数形结合解答问题..
15.(2009山东卷理)不等式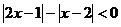 的解集为
.
的解集为
. 

答案 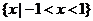
解析 原不等式等价于不等式组①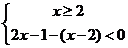 或②
或②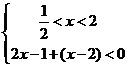
或③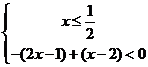 不等式组①无解,由②得
不等式组①无解,由②得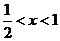 ,由③得
,由③得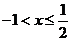 ,综上得
,综上得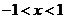 ,所以原不等式的解集为
,所以原不等式的解集为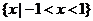 .
.
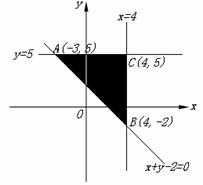
14.(2009北京卷理)若实数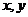 满足
满足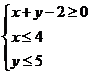 则
则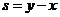 的最小值为__________.
的最小值为__________.
答案 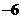


解析 本题主要考查线性规划方面
的基础知. 属于基础知识、基本运算
的考查.
如图,当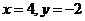 时,
时, 

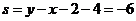 为最小值.
为最小值.
故应填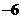 .
.
13.(2009北京文)若实数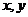 满足
满足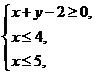 则
则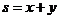 的最大值为
.
的最大值为
.
答案 9
解析:本题主要考查线性规划方面的基础知. 属于基础知识、基本运算的考查. 

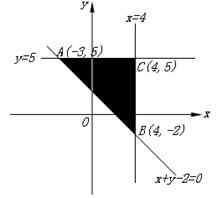 如图,当
如图,当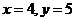 时,
时,
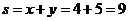 为最大值.
为最大值. 

故应填9.
12.(2009浙江卷文)若实数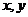 满足不等式组
满足不等式组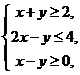 则
则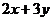 的最小
的最小
是 .
[命题意图]此题主要是考查了线性规划中的最值问题,此题的考查既体现了正确画线性区域的要求,也体现了线性目标函数最值求解的要求
解析 通过画出其线性规划,可知直线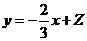 过点
过点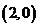 时,
时,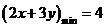
11.(2009浙江理)若实数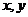 满足不等式组
满足不等式组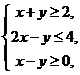 则
则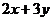 的最小值是
.
的最小值是
.
答案 4
解析 通过画出其线性规划,可知直线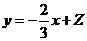 过点
过点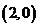 时,
时,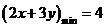
10.(2009福建卷文)在平面直角坐标系中,若不等式组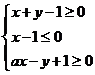 (
(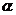 为常数)所表示的平面区域内的面积等于2,则
为常数)所表示的平面区域内的面积等于2,则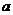 的值为
的值为
A. -5 B. 1 C. 2 D. 3
答案 D
解析 如图可得黄色即为满足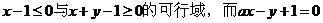 的直线恒过(0,1),故看作直线绕点(0,1)旋转,当a=-5时,则可行域不是一个封闭区域,当a=1时,面积是1;a=2时,面积是
的直线恒过(0,1),故看作直线绕点(0,1)旋转,当a=-5时,则可行域不是一个封闭区域,当a=1时,面积是1;a=2时,面积是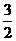 ;当a=3时,面积恰好为2,故选D.
;当a=3时,面积恰好为2,故选D.
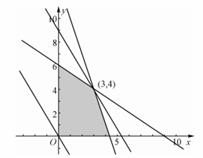
9.(2009四川卷理)某企业生产甲、乙两种产品,已知生产每吨甲产品要用A原料3吨、B 原料2吨;生产每吨乙产品要用A原料1吨、B原料3吨。销售每吨甲产品可获得利润5万元,每吨乙产品可获得利润3万元,该企业在一个生产周期内消耗A原料不超过13吨,B原料不超过18吨,那么该企业可获得最大利润是
A. 12万元 B. 20万元 C. 25万元 D. 27万元


答案 D
[考点定位]本小题考查简单的线性规划,基础题。(同文10)
解析 设甲、乙种两种产品各需生产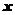 、
、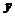 吨,可使利润
吨,可使利润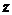 最大,故本题即
最大,故本题即
 已知约束条件
已知约束条件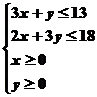 ,求目标函数
,求目标函数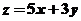 的最大
的最大
值,可求出最优解为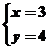 ,故
,故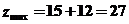 ,故选
,故选
择D。
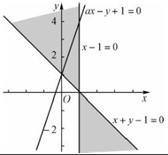
8.(2009天津卷理)设变量x,y满足约束条件: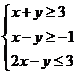 .则目标函数z=2x+3y的最小值为
.则目标函数z=2x+3y的最小值为
A.6 B.7 C.8 D.23
答案 B
[考点定位]本小考查简单的线性规划,基础题。
解析 画出不等式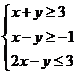 表示的可行域,如右图,
表示的可行域,如右图, 

让目标函数表示直线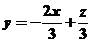 在可行域上平移,知在点B自目标函数取到最小值,解方程组
在可行域上平移,知在点B自目标函数取到最小值,解方程组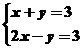 得
得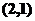 ,所以
,所以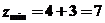 ,故选择B。
,故选择B。


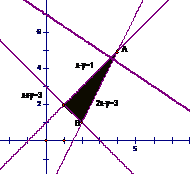
7.(2009湖南卷理)已知D是由不等式组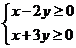 ,所确定的平面区域,则圆
,所确定的平面区域,则圆 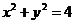 在区域D内
在区域D内
的弧长为 [ B]
A .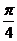 B.
B.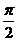 C.
C.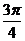 D.
D.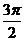
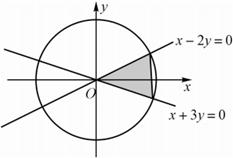


答案 B
解析
解析如图示,图中阴影部分所在圆心角所对弧长即为所求,易知图中两直线的斜率分别是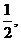
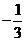 ,所以圆心角
,所以圆心角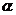 即为两直线的所成夹角,所以
即为两直线的所成夹角,所以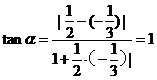 ,所以
,所以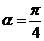 ,而圆的半径是2,所以弧长是
,而圆的半径是2,所以弧长是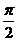 ,故选B现。
,故选B现。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com