
7.(2009湖南卷文)设函数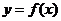 在
在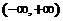 内有定义,对于给定的正数K,定义函数
内有定义,对于给定的正数K,定义函数 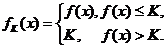
取函数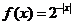 。当
。当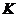 =
=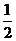 时,函数
时,函数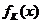 的单调递增区间为 (
)
的单调递增区间为 (
)
A
.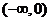 B.
B.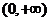 C .
C .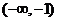 D .
D .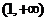
答案 C
解析 函数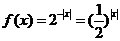 ,作图易知
,作图易知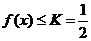
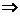
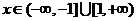 ,
,
故在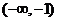 上是单调递增的,选C.
上是单调递增的,选C.
6.(2009湖南卷文)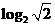 的值为
的值为
A.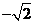 B.
B.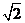 C.
C.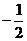 D.
D. 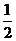
答案 D
解析 由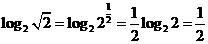 ,易知D正确.
,易知D正确.
5.(2009全国卷Ⅱ理)设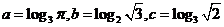 ,则
,则
A. 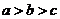 B.
B. 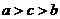 C.
C.
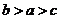 D.
D.
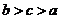
答案 A
解析 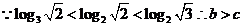
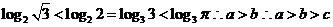 .
.
4.(2009四川卷文)函数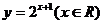 的反函数是
的反函数是
A. 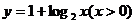 B.
B.
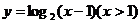
C. 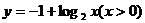 D.
D.
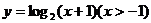
答案 C
解析 由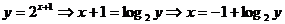 ,又因原函数的值域是
,又因原函数的值域是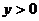 ,
,
∴其反函数是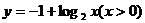
3.(2009天津卷文)设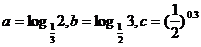 ,则 ( )
,则 ( )
A a<b<c B a<c<b C b<c<a D b<a<c
答案 B
解析 由已知结合对数函数图像和指数函数图像得到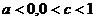 ,而
,而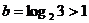 ,因此选B。
,因此选B。
[考点定位]本试题考查了对数函数和指数函数的性质运用,考查了基本的运算能
2.(2009北京文)为了得到函数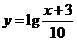 的图像,只需把函数
的图像,只需把函数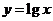 的图像上所有
的图像上所有
点 ( )
A.向左平移3个单位长度,再向上平移1个单位长度
B.向右平移3个单位长度,再向上平移1个单位长度
C.向左平移3个单位长度,再向下平移1个单位长度
D.向右平移3个单位长度,再向下平移1个单位长度
答案 C
.w 解析 本题主要考查函数图象的平移变换. 属于基础知识、基本运算的考查.
2009年高考题
1.(2009年广东卷文)若函数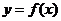 是函数
是函数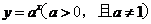 的反函数,且
的反函数,且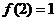 ,则
,则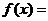 ( )
( )
A.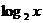 B.
B.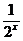 C.
C.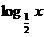 D.2
D.2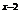
答案 A
解析
函数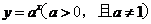 的反函数是
的反函数是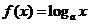 ,又
,又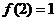 ,即
,即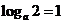 ,
,
所以,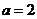 ,故
,故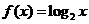 ,选A.
,选A.
8.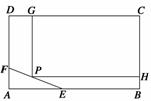 (陕西长安二中2008届高三第一学期第二次月考)为了保护环境,实现城市绿化,某房地产公司要在拆迁地长方形
(陕西长安二中2008届高三第一学期第二次月考)为了保护环境,实现城市绿化,某房地产公司要在拆迁地长方形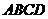 上规划出一块长方形地面建造公园,公园一边落在CD 上,但不得越过文物保护区
上规划出一块长方形地面建造公园,公园一边落在CD 上,但不得越过文物保护区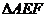 的EF.问如何设计才能使公园占地面积最大,并求这最大面积( 其中AB=200 m,BC=160 m,AE=60 m,AF=40 m.)
的EF.问如何设计才能使公园占地面积最大,并求这最大面积( 其中AB=200 m,BC=160 m,AE=60 m,AF=40 m.)
解 设CG=x,矩形CGPH面积为y,
如图作EN⊥PH于点N,则
∴HC=160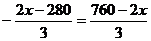
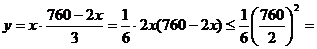
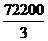
当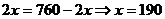 (m)即CG长为190m时,最大面积为
(m)即CG长为190m时,最大面积为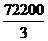 (m2)
(m2)
7.(四川省成都市新都一中高2008级一诊适应性测试)某机床厂今年年初用98万元购进一台
数控机床,并立即投入生产使用,计划第一年维修、保养费用12万元,从第二年开始,每年所需维修、保养费用比上一年增加4万元,该机床使用后,每年的总收入为50万元,设使用x年后数控机床的盈利额为y万元.
(1)写出y与x之间的函数关系式;
(2)从第几年开始,该机床开始盈利(盈利额为正值);
(3)使用若干年后,对机床的处理方案有两种:(Ⅰ)当年平均盈利额达到最大值时,以30万元价格处理该机床;(Ⅱ)当盈利额达到最大值时,以12万元价格处理该机床.
请你研究一下哪种方案处理较为合理?请说明理由.
解 (1)依题得: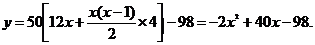 (x
(x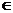 N*)
N*)
(2)解不等式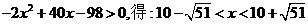
∵x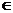 N*,∴3≤x≤17,故从第3年开始盈利。
N*,∴3≤x≤17,故从第3年开始盈利。
(3)(Ⅰ)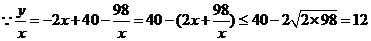
当且仅当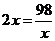 时,即x=7时等号成立.
时,即x=7时等号成立.
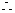 到2008年,年平均盈利额达到最大值,工厂共获利12×7+30=114万元.
到2008年,年平均盈利额达到最大值,工厂共获利12×7+30=114万元.
(Ⅱ)y=-2x2+40x-98=-(x-10)2+102,当x=10时,ymax=102
故到2011年,盈利额达到最大值,工厂获利102+12=114万元
盈利额达到的最大值相同,而方案Ⅰ所用的时间较短,故方案Ⅰ比较合理.
6.( 2008年高考数学各校月考试题)某公司以每吨10万元的价格销售某种化工产品,每年可售出该产品1000吨,若将该产品每吨的价格上涨x%,则每年的销售数量将减少mx%,其中m为正常数.
(1)当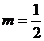 时,该产品每吨的价格上涨百分之几,可使销售的总金额最大?
时,该产品每吨的价格上涨百分之几,可使销售的总金额最大?
(2)如果涨价能使销售总金额增加,求m的取值范围.
解(1)由题设,当价格上涨x%时,销售总金额为:
(2)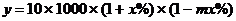 (万元)
(万元)
即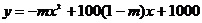 。
。
当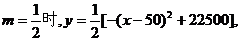
当x=50时,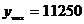 万元.
万元.
即该吨产品每吨的价格上涨50%时,销售总最大.
(2)由(1)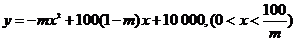
如果上涨价格能使销假售总金额增加,
则有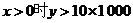
即x>0时,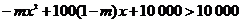
∴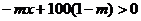
注意到m>0
∴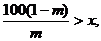 ∴
∴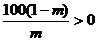 ∴
∴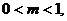
∴m的取值范围是(0,1)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com