
6.(湖北省黄冈市2009年3月份高三年级质量检测文)设函数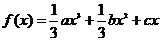
(c<0)单调递增区间是 .
答案 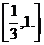
5. (北京市东城区2009年3月高中示范校高三质量检测理)已知函数f(x)的定义域为[-2,+∞),部分对应值如下表,
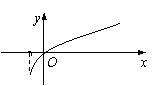
(北京市东城区2009年3月高中示范校高三质量检测理)已知函数f(x)的定义域为[-2,+∞),部分对应值如下表,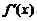 为f(x)的导函数,函数
为f(x)的导函数,函数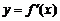 的图象如右图所示,若两正数a,b满足
的图象如右图所示,若两正数a,b满足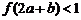 ,则
,则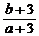 的取值范围是 .
的取值范围是 .
答案 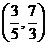
4.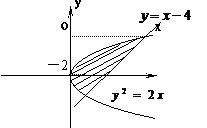 (2009年乐陵一中)图中,阴影部分的面积是
( )
(2009年乐陵一中)图中,阴影部分的面积是
( )
A.16 B.18
C.20 D.22
答案 B
3.(2009嘉兴一中一模)下列图像中有一个是函数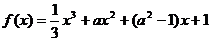
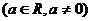 的导数
的导数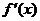 的图像,则
的图像,则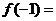 ( )
( )
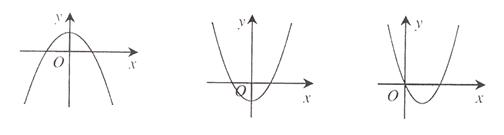
A.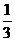 B.
B.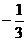 C.
C.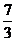 D.
D.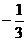 或
或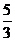
答案 B
2.(2009天津重点学校二模)已知函数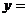
 是定义在R上的奇函数,且当
是定义在R上的奇函数,且当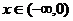
时不等式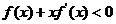 成立, 若
成立, 若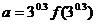 ,
,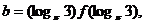
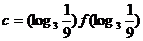 ,则
,则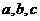 的大小关系是 ( )
的大小关系是 ( )
A.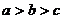 B.
B.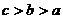 C.
C.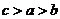 D.
D.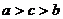
答案 C
1.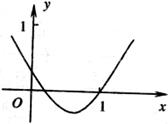 (2009威海二模)右图是函数f(x)=x2+ax+b的部分图象,则
(2009威海二模)右图是函数f(x)=x2+ax+b的部分图象,则
函数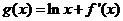 的零点所在的区间是
( )
的零点所在的区间是
( )
A.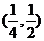 B.
B.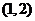
C.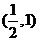 D.
D.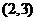
答案 C
2009年联考题
25.( 2005年全国卷III)用长为90cm,宽为48cm的长方形铁皮做一个无盖的容器,先在四角
分别截去一个小正方形,然后把四边翻转90°角,再焊接而成(如图),问该容器的高为多少时,容器的容积最大?最大容积是多少?
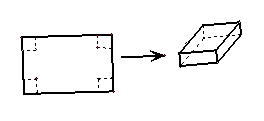 解 设容器的高为x,容器的体积为V,1分
解 设容器的高为x,容器的体积为V,1分
则V=(90-2x)(48-2x)x,(0<V<24) 5分
=4x3-276x2+4320x
∵V′=12x2-552x+4320…… 7分
由V′=12x2-552x+4320=0得x1=10,x2=36
∵x<10 时,V′>0,
10<x<36时,V′<0,
x>36时,V′>0,
所以,当x=10,V有极大值V(10)=1960…………………………………………………10分
又V(0)=0,V(24)=0, ……………………………………………………………………11分
所以当x=10,V有最大值V(10)=1960 …………………………………………………12分
24.(2005年安徽卷)设函数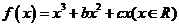 ,已知
,已知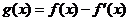 是奇
是奇
函数。
(Ⅰ)求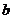 、
、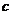 的值。
的值。
(Ⅱ)求 的单调区间与极值。
的单调区间与极值。
解
(Ⅰ)∵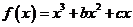 ,∴
,∴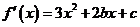 .从而
.从而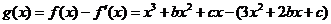 =
=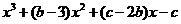
是一个奇函数,所以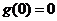 得
得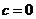 ,由奇函数定义得
,由奇函数定义得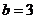 ;
;
(Ⅱ)由(Ⅰ)知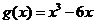 ,从而
,从而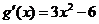 ,由此可知,
,由此可知,
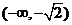 和
和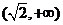 是函数
是函数 是单调递增区间;
是单调递增区间;
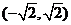 是函数
是函数 是单调递减区间;
是单调递减区间;
 在
在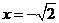 时,取得极大值,极大值为
时,取得极大值,极大值为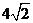 ,
, 在
在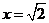 时,取得极小值,极小值为
时,取得极小值,极小值为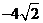 。
。
23.(2008年天津卷21)(本小题满分14分)
已知函数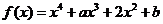 (
(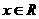 ),其中
),其中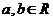 .
.
(Ⅰ)当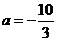 时,讨论函数
时,讨论函数 的单调性;
的单调性;
(Ⅱ)若函数 仅在
仅在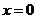 处有极值,求
处有极值,求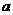 的取值范围;
的取值范围;
(Ⅲ)若对于任意的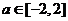 ,不等式
,不等式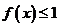 在
在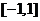 上恒成立,求
上恒成立,求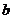 的取值范围.
的取值范围.
本小题主要考查利用导数研究函数的单调性、函数的最大值、解不等式等基础知识,考查综合分析和解决问题的能力.满分14分.
(Ⅰ)解析 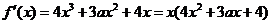 .
.
当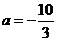 时,
时,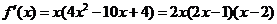 .
.
令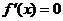 ,解得
,解得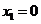 ,
,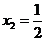 ,
,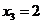 .
.
当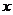 变化时,
变化时,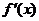 ,
, 的变化情况如下表:
的变化情况如下表:
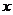 |
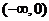 |
0 |
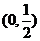 |
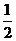 |
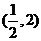 |
2 |
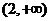 |
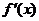 |
- |
0 |
+ |
0 |
- |
0 |
+ |
 |
↘ |
极小值 |
↗ |
极大值 |
↘ |
极小值 |
↗ |
所以 在
在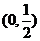 ,
,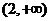 内是增函数,在
内是增函数,在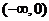 ,
,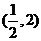 内是减函数.
内是减函数.
(Ⅱ)解析 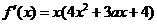 ,显然
,显然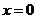 不是方程
不是方程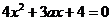 的根.
的根.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com