
2.函数 的最小正周期是( )
的最小正周期是( )
A. B.
B.
 C.
C. D.
D.
1.已知 ,
, , 则
, 则 ·
· 等于( )
等于( )
A. 0
B. 10
C. 6
D. 
16. (本小题共13分)
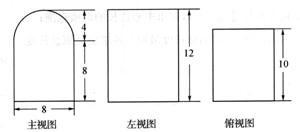
已知某个几何体的三视图如图(主视图的弧线是半圆),根据图中标出的数据,
(Ⅰ)求这个组合体的体积;
(Ⅱ)若组合体的底部几何体记为 ,其中
,其中 为正方形.
为正方形.
(i)求证: ;
;
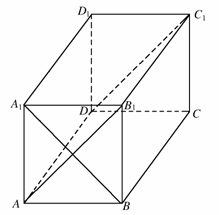 (ii)求证:
(ii)求证: 为棱
为棱 上一点,求
上一点,求 的最小值.
的最小值.
17.(本小题满分13分)
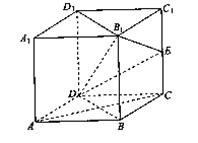
 如图,已知四棱柱ABCD-A1B1C1D1的底面是菱形,侧棱BB1⊥底面ABCD,E是侧棱CC1的中点。
如图,已知四棱柱ABCD-A1B1C1D1的底面是菱形,侧棱BB1⊥底面ABCD,E是侧棱CC1的中点。
(I)求证:AC⊥平面BDD1B1;
(II)求证:AC//平面B1DE。
16、
 (13分)如图,在四棱锥
(13分)如图,在四棱锥 中,底面
中,底面 是菱形,
是菱形, ,
, 为
为 的中点,
的中点, 为
为 的中点.
的中点.
(Ⅰ)证明:平面
 平面
平面 ;
;
(Ⅱ)证明:直线 .
.
17.(本小题满分14分)
如图,四棱锥 中,
中, 平面
平面 ,底面
,底面 为矩形,
为矩形, ,
, ,
, 为
为 的中点.
的中点.
(Ⅰ)求证: ;
;
(Ⅱ)求三棱锥 的体积;
的体积;
(Ⅲ) 边上是否存在一点
边上是否存在一点 ,使得
,使得 平面
平面 ,若存在,求出
,若存在,求出 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
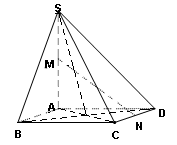
(17) (本题满分13分)
如图,在四棱锥 中,底面
中,底面 是正方形,其他四个侧面都是等边三角形,
是正方形,其他四个侧面都是等边三角形, 与
与 的交点为O.
的交点为O.
(Ⅰ)求证: 平面
平面 ;
;
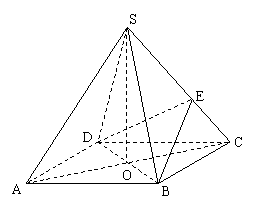 (Ⅱ)已知
(Ⅱ)已知 为侧棱
为侧棱 上一个动点. 试问对于
上一个动点. 试问对于 上任意一点
上任意一点 ,平面
,平面 与平面
与平面 是否垂直?若垂直,请加以证明;若不垂直,请
是否垂直?若垂直,请加以证明;若不垂直,请 说明理由.
说明理由.
(16)(本小题共14分)]
 正方体
正方体 的棱长为
的棱长为 ,
, 是
是 与
与 的
的 交点,
交点, 为
为 的中点.
的中点.
(Ⅰ)求证:直线 ∥平面
∥平面 ;
;
(Ⅱ)求 证:
证: 平面
平面 ;
;
(Ⅲ)求三棱锥 的体积.
的体积.
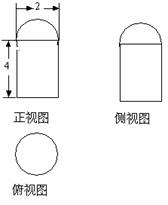
12. 已知一个空间几何体的三视图如图所示,其中正视图、侧视图都是由半圆和矩形组成,根据图中标出的尺寸,计算这个几何体的表面积是 .
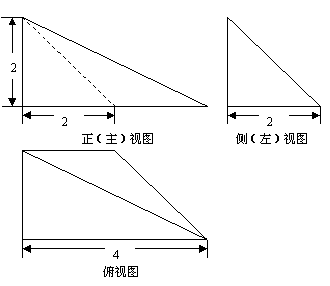 (2)一个几何体的三视图如图所示,则这个几何体的体积等于
(2)一个几何体的三视图如图所示,则这个几何体的体积等于
(A)  (B)
(B)  (C)
(C) (D)
(D)
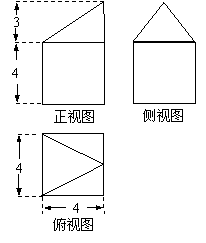
(7)一个几何体的三视图如图所示,则此几何体的体积是
(A) (B)
(B)
 (C)
(C) (D)
(D)
17.(本小题满分14分)
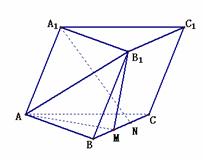 在斜三棱柱
在斜三棱柱 中,侧面
中,侧面
 平面
平面 ,
, .
.
(I)求证: ;
;
(II)若M,N是棱BC上的两个三等分点,
求证: 平 面
平 面 .
.
5.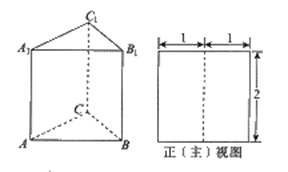 如图,三棱柱ABC-A1B1C1的侧棱长和底面边长均为2,且侧棱
如图,三棱柱ABC-A1B1C1的侧棱长和底面边长均为2,且侧棱 底面ABC,其正(主)视图是边长为2的正方形,则此三棱柱侧(左)视图
底面ABC,其正(主)视图是边长为2的正方形,则此三棱柱侧(左)视图 的面积为 ( )
的面积为 ( )
A.
B.
C.
D.4
3. 已知 ,
, 为两条不同的直线,
为两条不同的直线, ,
, 为两个不同的平面,则下列命题中正确的是( A )
为两个不同的平面,则下列命题中正确的是( A )
A . B.
B. 
C. D.
D. 
(4)一个正方体的所有顶点都在同一球面上,若球的体积是 ,则正方体的表面积是
,则正方体的表面积是
(A)8 (B)6 (C)4 (D)3
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com