第一节 (共5小题；每小题1.5分，满分7.5分)

1. How was the concert?　

A. Boring.　 B. Dull.　 C. Wonderful.

2. What is the exact time now?　

A. 9:37.　 B. 9:35.　 C. 9:39.

3. Where was the man last weekend?　

　A. In his sister’s.　 B. At home.　 C. In the 4^th street.

4. What’s Susan like?

　A. She is very honest.　 B. She is very clever.　 C. She is very capable.

5. What does the lady like to drink?　

A. Tea.　 B. Coffee.　 C. Orange juice.

20. [解析]本题是关于椭圆、圆、直线的综合问题，解决的关键是确定圆心的坐标。

⑴由题意有．…2分设,由为等腰三角形,则只能是,又，即,所以．…6分

⑵由题意得椭圆的方程为，其离心率为，此时．　　

由，可得．…10分，设内切圆的圆心，，因为为等腰三角形，所以的内切圆的圆心点到的距离等于点到轴的距离，即，　 ① 由点在直线上，所以，　　 ②

由①②可得所以的内切圆的方程为

.16分.点评：本题亦可先用面积求出半径，再求圆的方程．本题属于中档题，计算量稍大。

19、(本题满分16分)

解：(1)长轴长26，右准线方程………4分(2)抛物线…8分

(3)设，由题意知，..11分

……13分

(4)最小值为21…………………………16分

18、解:(1)由题意知此平面区域表示的是以构成的三角形及其内部,且△是直角三角形,…3分，所以覆盖它的且面积最小的圆是其外接圆,故圆心是(2,1),半径是,…5分

所以圆的方程是.…7分

　 (2)设直线的方程是:..8分因为,所以圆心到直线的距离是_..10分

即……12分解得:.……13分

所以直线的方程是:.………15分注：用第二问结论参照得分。

17．(1),

，面；…5分

(2)

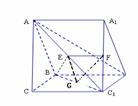
……10分

(3)G为中点…………………11分

……………………15分

16．解：(1)∵B(0,-b)，A(∵2　 ∴D为线段FP的中点　 1分　

∴(c,即A、B、D共线2分　∴而?,?∴(得a=2b∴e=　 4分?

　(Ⅱ)∵a=2而e=双曲线方程为①5分∴B(0,-1)　

假设存在定点C(0,n)使为常数u，　设MN的方程为y=kx-1　 ②　 6分　

由②代入①得由题意得得

设M(?　 8分　

而?　

=?

整理得：［4］［8-］=0　　 10分

对满足　∴解得n=4,u=17　

故存在y轴上的定点C(0,4),使为常数17　　 14分

15．(1)-------4(2) 或-------4

(3) 和-------4

8. ①②③ 9. 10.11. 　12. 13. 　14. 　

1． 　2. 　3. R, >0　 4. 　5. 　6. () 7.

20. (本题满分16分)已知椭圆的左、右焦点分别为，其右准线上上存在点(点在 轴上方)，使为等腰三角形．⑴求离心率的范围；⑵若椭圆上的点到两焦点的距离之和为，求的内切圆的方程．

苏州市2009-2010学年度第二学期模块过关试题

高 二 数 学