
2、某矿泉水标签上印有水质成分如下(mg/L): 硒:0.013;锶:0.0596;锌:0.00162;钠:18.4;钙:4.69。这里的硒、锶、锌、钠、钙是指( )
A.金属 B.分子
C.原子 D.元素
1、下列各图所示变化属于物理变化的是 ( )

例4 (2007年高考全国卷Ⅱ理科22题)已知函数f (x)=x3-x.
(Ⅰ)求曲线y=f (x)在点M(t,f (t))处的切线方程;
(Ⅱ)设a>0,如果过点(a,b)可作曲线y=f (x)的三条切线,证明:-a<b<f (a).
分析 (Ⅰ)问比较简单,f ¢(x0)的几何意义是曲线f(x)在点(x0,f (x0))处的切线的斜率,利用这一几何意义就可以求切线方程.(Ⅱ)问中条件“过点可作曲线y=f (x)的三条切线”,可转化为该点代入切线方程后所得方程有三个相异的实根,而研究根的个数仍然需要借助导数.
解 (Ⅰ)求函数f (x)的导数:f ¢(x)=3x2-1.
曲线y=f (x)在点M(t,f (t))处的切线方程为:y-f (t)=f ¢(t)(x-t),
即y=(3t2-1)x-2t3.
(Ⅱ)如果有一条切线过点(a,b),则存在t,使b=(3t2-1)a-2t3.
于是,若过点(a,b)可作曲线y=f (x)的三条切线,则方程2t3-3at2+a+b=0有三个相异的实数根.
记g(t)= 2t3-3at2+a+b,则g¢(t)=6t2-6at=6t(t-a).
当t变化时,g(t),g¢(t)变化情况如下表:
|
t |
(-¥,0) |
0 |
(0,a) |
a |
(a,+¥) |
|
g¢(t) |
+ |
0 |
- |
0 |
+ |
|
g(t) |
↗ |
极大值a+b |
↘ |
极小值b-f (a) |
↗ |
由g(t)的单调性,当极大值a+b<0或极小值b-f (a)>0时,方程g(t)=0最多有一个实数根;
当a+b=0时,解方程g(t)=0得 ,即方程g(t)=0只有两个相异的实数根;
,即方程g(t)=0只有两个相异的实数根;
当b-f (a)=0时,解方程g(t)=0得 ,即方程g(t)=0只有两个相异的实数根.
,即方程g(t)=0只有两个相异的实数根.
综上,如果过(a,b)可作曲线y=f (x)三条切线,即g(t)=0有三个相异的实数根,则 即-a<b<f (a).
即-a<b<f (a).
点评 利用导数研究一个三次方程f (x)=0根的个数问题是一类常见的题型,它可以看成是函数f (x)的图像与x轴的交点个数问题,因此与函数的极值有关.
由此可见,我们常常利用导数判断函数的单调性、求极值、求最值、求取值范围、证明不等式、求切线方程、判断方程根的个数,而这七个应用我们通过上面四个典型例题就可以学到.
例3 (2007年高考安徽卷理科18题)设a≥0,f (x)=x-1-ln2 x+2aln x(x>0).
(Ⅰ)令F(x)=x f ¢(x),讨论F(x)在(0,+¥)内的单调性并求极值;
(Ⅱ)求证:当x>1时,恒有x>ln2 x-2aln x+1.
分析 利用导数研究函数的单调性、极值和证明不等式是近年来高考中的常考题型,解题时有一套完整的流程,我们必须十分熟练.
(Ⅰ)解 根据求导法则有 ,
,
故F(x)=x f ¢(x)=x-2ln x+2a(x>0),于是 ,
,
列表如下:
|
x |
(0,2) |
2 |
(2,+¥) |
|
F¢(x) |
- |
0 |
+ |
|
F(x) |
↘ |
极小值F(2) |
↗ |
故知F(x)在(0,2)内是减函数,在(2,+¥)内是增函数,所以,在x=2处取得极小值F(2)=2-2ln2+2a.
(Ⅱ)证明 由a≥0知,F(x)的极小值F(2)=2-2ln2+2a>0.
于是由上表知,对一切x∈(0,+¥),恒有F(x)=x f ¢(x)>0.
从而当x>0时,恒有f ¢(x)>0,故f (x)在(0,+¥)内单调增加.
所以当x>1时,f (x)>f (1)=0,即x-1-ln2 x+2aln x>0.
故当x>1时,恒有x>ln2 x-2aln x+1.
点评 本题主要考查函数导数的概念与计算,利用导数研究函数的单调性、极值和证明不等式的方法,考查综合运用有关知识解决问题的能力.需要注意的是(Ⅱ)问中的不等式经移项后不必构造新的函数,因为这就是已知函数f (x),并且f (x)的单调性也不用再求导研究,因为可以利用(Ⅰ)问中F(x)的单调性和极小值就可以找到f ¢(x)>0,从而得出f (x)的单调性.
例2 (2007年高考全国卷Ⅰ理科20题)设函数 .
.
(Ⅰ)证明:f (x)的导数f ¢(x)≥2;
(Ⅱ)若对所有x≥0都有f (x)≥ax,求a的取值范围.
分析 本题(Ⅰ)比较简单,用均值不等式可一步到位;(Ⅱ)需要先把不等式移项之后,构造新的函数,通过对新函数求导来研究其单调性从而确定参数的范围.
(Ⅰ)证明 f (x)的导数 .
.
由于 ,故f ¢(x)≥2.(当且仅当x=0时,等号成立.)
,故f ¢(x)≥2.(当且仅当x=0时,等号成立.)
(Ⅱ)解 令g(x)=f (x)-ax,则g¢(x)=f ¢(x)-a= .
.
(ⅰ)若a≤2,当x>0时, ,
,
故g(x)在(0,+¥)上为增函数.
所以,对x≥0时,g(x)≥g(0)=0,即f (x)≥ax.
(ⅱ)若a>2,方程g¢(x)=0的正根为 ,
,
此时,若x∈(0,x1),则g¢(x)<0,故g(x)在该区间为减函数.
所以,x∈(0,x1)时,g(x)<g(0)=0,即f (x)<ax,与题设f (x)≥ax相矛盾.
综上,满足条件的a的取值范围是(-¥,2].
点评 需要提醒大家的是,初步得出a的取值范围为a≤2还不完整,还需继续说明当a不在此范围内时,即当a>2时为什么不行,等找到矛盾后才能彻底说明范围a≤2是原条件的充要条件.
例1某分公司经销某种品牌产品,每件产品的成本为3元,并且每件产品需向总公司交a元(3≤a≤5)的管理费,预计当每件产品的售价为x元(9≤x≤11)时,一年的销售量为 (12-x)2万件.
(Ⅰ)求分公司一年的利润L(万元)与每件产品的售价x的函数关系式;
(Ⅱ)当每件产品的售价为多少元时,分公司一年的利润L最大,并求出L的最大值Q(a).
分析 本题列出利润函数的关系式并不难,但由于函数是三次的,所以要求出最大的利润还需借助导数知识.
解 (Ⅰ)分公司一年的利润L(万元)与售价x的函数关系式为
L(x)=(x-3-a)(12-x)2,x∈[9,11].
(Ⅱ)L¢(x)=(12-x)2-2(x-3-a)(12-x)
=(12-x)(18+2a-3x).
令L¢(x)=0得 ,或x=12(不合题意,舍去).
,或x=12(不合题意,舍去).
∵3≤a≤5,∴8≤ ≤
≤ .
.
(1)当8≤ <9即3≤a<
<9即3≤a< 时,在[9,11]上L¢(x)<0,L(x)为减函数,
时,在[9,11]上L¢(x)<0,L(x)为减函数,
所以Lmax=L(9)=(9-3-a)(12-9)2=9(6-a).
(2)当9≤ ≤
≤ 即
即 ≤a≤5时,在
≤a≤5时,在 两侧L¢的值由正变负,L(x)由增函数变减函数,
两侧L¢的值由正变负,L(x)由增函数变减函数,
所以 .
.
综上所述,最大利润
答:若3≤a< ,则当每件售价为9元时,分公司一年的利润L最大,且最大值Q(a)=9(6-a)(万元);若
,则当每件售价为9元时,分公司一年的利润L最大,且最大值Q(a)=9(6-a)(万元);若 ≤a≤5,则当每件售价为
≤a≤5,则当每件售价为 元时,分公司一年的利润L最大,且最大值
元时,分公司一年的利润L最大,且最大值 (万元).
(万元).
点评 本题考查了函数、导数及其应用等知识,考查了运用数学知识分析和解决实际问题的能力,还体现了分类讨论的思想方法.
7、已知数列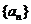 与圆
与圆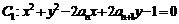 和圆
和圆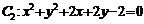 ,若圆
,若圆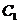 与圆
与圆 交于
交于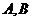 两点且这两点平分圆
两点且这两点平分圆 的周长.
的周长.
(1)求证:数列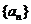 是等差数列;(2)若
是等差数列;(2)若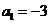 ,则当圆
,则当圆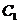 的半径最小时,求出圆
的半径最小时,求出圆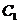 的方程.
的方程.
6、已知⊙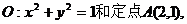 由⊙O外一点P(a,b)向⊙O引切线PQ,切点为
由⊙O外一点P(a,b)向⊙O引切线PQ,切点为
Q,且满足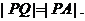
(1)求实数a,b间满足的等量关系;
(2)求线段PQ长的最小值;
(3)若以P为圆心所作的⊙P与⊙O有公共点,试求半径最小值时⊙P的方程。
5、 已知两点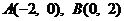 ,点
,点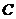 是圆
是圆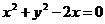 上任意一点,则
上任意一点,则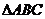 面积的最小值是
面积的最小值是
4、
已知圆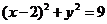 和直线
和直线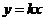 交于A,B两点,O是坐标原点, 若
交于A,B两点,O是坐标原点, 若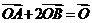 ,则
,则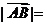 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com