
(Ⅰ)证明:直线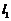 和
和 的斜率之积为定值;
的斜率之积为定值;
(Ⅱ)求点M的轨迹方程。
解:(I)依题意,直线l的斜率存在,设直线l的方程为y=kx+p
17、(北京市西城区2008年5月高三抽样测试)已知抛物线的方程为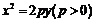 ,过点
,过点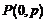 的直线
的直线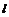 与抛物线相交于A、B两点,分别过点A、B作抛物线的两条切线
与抛物线相交于A、B两点,分别过点A、B作抛物线的两条切线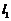 和
和 的斜率之积为定值;
的斜率之积为定值;
综上,在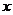 轴上存在定点
轴上存在定点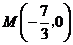 ,使
,使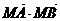 为常数.
为常数.
当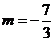 时, 亦有
时, 亦有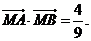 ………….. 13分
………….. 13分
② 当直线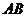 与
与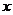 轴垂直时,此时点
轴垂直时,此时点 的坐标分别为
的坐标分别为 ,
,
注意到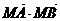 是与
是与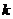 无关的常数, 从而有
无关的常数, 从而有 , 此时
, 此时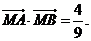 .. 11分
.. 11分
将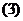 代入,整理得
代入,整理得 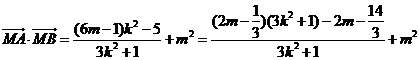
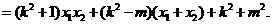 …………..
8分
…………..
8分
所以
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com