⑴获得亲身参与研究探索的体验，

⑵培养提出问题和解决问题的能力，

⑶培养收集、分析和利用信息的能力，

⑷学会分享与合作，

⑸培养科学研究的志趣、态度和社会使命感。

4、交流

各组间进行交流，并进行评比，产生优秀研究小组并加以奖励。

3、分工调查

由组长安排，组员间发挥通力协作的精神，分工合作完成数据采集，分析，整理等工作，并形成调查报告。

2、分组申报

按每班人数合理分组，由组员选择研究性课题并加以申报。

1、给出参考课题

⑴ 气象学中的数学应用问题

⑵ 有关房子粉刷的预算

⑶ 日常生活中的悖论问题

⑷ 投资人寿保险和投资银行的分析比较

⑸ 环境规划与数学

⑹ 如何计算一份试卷的难度与区分度

⑺ 数学的发展历史

⑻ 给人与人的关系(友情)评分

⑼ 丈量方圆大厦

⑽ 如何存款最合算

⑾ 哪家超市最便宜

⑿ 计算器对运算能力影响

⒀ 出租车车费的合理定价

⒁ 衣服的价格、质地、品牌，左右消费者观念多少？

根据所学知识研究日常生活中的问题

2006年9月11日--2006年12月10日

∴a_­²+b²+c²＜2(ab+bc+ca)

2、利用分析法，结合三角形的边角关系和同向正则不等式可以相乘的性质可以得到

证法三：∵a,b,c为△ABC的三边

∴a＞0，b＞0，c＞0且a+b＞c，a+c＞b，b+c＞a

利用同向正则不等式可以相乘，得到

a(b+c)＞a² 　 b(a+c)＞b² c(a+b)＞c²

又∵ 2(ab+bc+ca)

　　 ＝ab+ac+bc+ba+bc+ac

　　 ＝a(b+c)+b(a+c)+c(a+b)＞a_­²+b²+c²

∴ a_­²+b²+c²＜2(ab+bc+ca)

在讨论题目的证明过程中，有的同学想到了这样的证明方法：

证法四∵a,b,c为△ABC的三边

∴a－b＜c， b－c＜a，a－c＜b

∴(a－b)²＜c²， (b－c)²＜a²，(a－c)²＜b²

上述三个不等式相得

(a－b)+(b－c)²+(a－c)²＜a_­²+b²+c²

即a_­²+b²+c²＜2(ab+bc+ca)

这种证明简明扼要，非常优秀，说明学生的思维是非常敏捷的。只是在三角形中由a－b＜c， b－c＜a，a－c＜b就一定推出(a－b)²＜c²， (b－c)²＜a²，(a－c)²＜b²的推理不严谨，师生共同改进证明方法可以得到下列优秀证法

证明：∵a,b,c为△ABC的三边

∴|a－b|＜c， |b－c|＜a，|a－c|＜b

∴(a－b)²＜c²， (b－c)²＜a²，(a－c)²＜b²

上述三个同向不等式相得

(a－b)+(b－c)²+(a－c)²＜a_­²+b²+c²

即a_­²+b²+c²＜2(ab+bc+ca)

题目证明完成后，进一步引申，可以得到下面的命题：

已知a,b,c为△ABC的三边,求证关于x的不等式

x²+(a+b+c)x+ab+ac+bc＞0的解集为R。

证明：∵ a,b,c为△ABC的三边

x²+(a+b+c)x+ab+ac+b

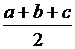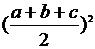＝(x+)²－+ab+ac+bc

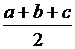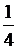＝(x+)²+(4(ab+bc+ac)－(a+b+c)²)

由前面的命题可知

(a+b+c)²－4(ab+ac+bc)

　 ＝a_­²+b²+c²－2(ab+bc+ca)

　　 ＝(a²－ab－ca)+(b²－ab－bc)+(c²－bc－ac)

　　 ＝a(a－b－c)+b(b－a－c)+c(c－b－a)

　　 ＝－(a(b+c－a)+b(a+c－b)+c(b+a－c))＜0

∴4(ab+bc+ac)－(a+b+c)²＞0

又∵(x+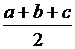)²＞0

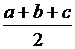∴(x+)²+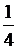(4(ab+bc+ac)－(a+b+c)²)＞0恒成立

∴关于x的不等式x²+(a+b+c)x+ab+ac+bc＞0的解集为R

4、　 重视数学应用

3、　 增加灵活性