
8、数列的极限
我们先来回忆一下初等数学中学习的数列的概念。
⑴、数列:若按照一定的法则,有第一个数a1,第二个数a2,…,依次排列下去,使得任何一个正整数n对应着一个确定的数an,那末,我们称这列有次序的数a1,a2,…,an,…为数列.数列中的每一个数叫做数列的项。第n项an叫做数列的一般项或通项.
注:我们也可以把数列an看作自变量为正整数n的函数,即:an=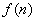 ,它的定义域是全体正整数
,它的定义域是全体正整数
⑵、极限:极限的概念是求实际问题的精确解答而产生的。
例:我们可通过作圆的内接正多边形,近似求出圆的面积。
设有一圆,首先作圆内接正六边形,把它的面积记为A1;再作圆的内接正十二边形,其面积记为A2;再作圆的内接正二十四边形,其面积记为A3;依次循下去(一般把内接正6×2n-1边形的面积记为An)可得一系列内接正多边形的面积:A1,A2,A3,…,An,…,它们就构成一列有序数列。我们可以发现,当内接正多边形的边数无限增加时,An也无限接近某一确定的数值(圆的面积),这个确定的数值在数学上被称为数列A1,A2,A3,…,An,… 当n→∞(读作n趋近于无穷大)的极限。
注:上面这个例子就是我国古代数学家刘徽(公元三世纪)的割圆术。
⑶、数列的极限:一般地,对于数列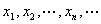 来说,若存在任意给定的正数ε(不论其多么小),总存在正整数N,使得对于n>N时的一切
来说,若存在任意给定的正数ε(不论其多么小),总存在正整数N,使得对于n>N时的一切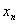 不等式
不等式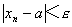 都成立,那末就称常数a是数列
都成立,那末就称常数a是数列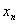 的极限,或者称数列
的极限,或者称数列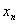 收敛于a .
收敛于a .
记作: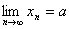 或
或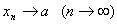
注:此定义中的正数ε只有任意给定,不等式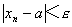 才能表达出
才能表达出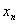 与a无限接近的意思。且定义中的正整数N与任意给定的正数ε是有关的,它是随着ε的给定而选定的。
与a无限接近的意思。且定义中的正整数N与任意给定的正数ε是有关的,它是随着ε的给定而选定的。
⑷、数列的极限的几何解释:在此我们可能不易理解这个概念,下面我们再给出它的一个几何解释,以使我们能理解它。数列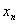 极限为a的一个几何解释:将常数a及数列
极限为a的一个几何解释:将常数a及数列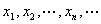 在数轴上用它们的对应点表示出来,再在数轴上作点a的ε邻域即开区间(a-ε,a+ε),如下图所示:
在数轴上用它们的对应点表示出来,再在数轴上作点a的ε邻域即开区间(a-ε,a+ε),如下图所示:
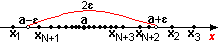 因不等式
因不等式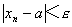 与不等式
与不等式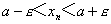 等价,故当n>N时,所有的点
等价,故当n>N时,所有的点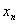 都落在开区间(a-ε,a+ε)内,而只有有限个(至多只有N个)在此区间以外。
都落在开区间(a-ε,a+ε)内,而只有有限个(至多只有N个)在此区间以外。
注:至于如何求数列的极限,我们在以后会学习到,这里我们不作讨论。
⑸、数列的有界性:对于数列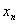 ,若存在着正数M,使得一切
,若存在着正数M,使得一切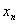 都满足不等式│
都满足不等式│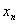 │≤M,则称数列
│≤M,则称数列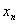 是有界的,若正数M不存在,则可说数列
是有界的,若正数M不存在,则可说数列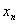 是无界的。
是无界的。
定理:若数列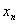 收敛,那末数列
收敛,那末数列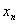 一定有界。
一定有界。
注:有界的数列不一定收敛,即:数列有界是数列收敛的必要条件,但不是充分条件。例:数列 1,-1,1,-1,…,(-1)n+1,… 是有界的,但它是发散的。
7、双曲函数及反双曲函数
⑴、双曲函数:在应用中我们经常遇到的双曲函数是:(用表格来描述)
|
函数的名称 |
函数的表达式 |
函数的图形 |
函数的性质 |
|
双曲正弦 |
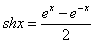 |
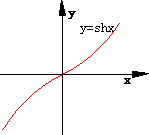 |
a):其定义域为:(-∞,+∞);
b):是奇函数;
c):在定义域内是单调增 |
|
双曲余弦 |
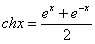 |
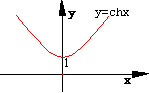 |
a):其定义域为:(-∞,+∞);
b):是偶函数;
c):其图像过点(0,1); |
|
双曲正切 |
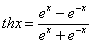 |
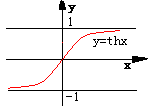 |
a):其定义域为:(-∞,+∞);
b):是奇函数;
c):其图形夹在水平直线y=1及y=-1之间;在定域内单调增; |
我们再来看一下双曲函数与三角函数的区别:
|
双曲函数的性质 |
三角函数的性质 |
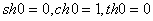 |
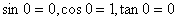 |
|
shx与thx是奇函数,chx是偶函数 |
sinx与tanx是奇函数,cosx是偶函数 |
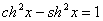 |
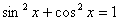 |
|
它们都不是周期函数 |
都是周期函数 |
双曲函数也有和差公式:
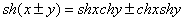
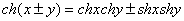
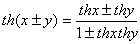
⑵、反双曲函数:双曲函数的反函数称为反双曲函数.
a):反双曲正弦函数 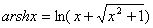 其定义域为:(-∞,+∞);
其定义域为:(-∞,+∞);
b):反双曲余弦函数
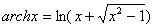 其定义域为:[1,+∞);
其定义域为:[1,+∞);
c):反双曲正切函数
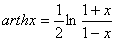 其定义域为:(-1,+1);
其定义域为:(-1,+1);
6、初等函数
⑴、基本初等函数:我们最常用的有五种基本初等函数,分别是:指数函数、对数函数、幂函数、三角函数及反三角函数。下面我们用表格来把它们总结一下:
|
函数名称 |
函数的记号 |
函数的图形 |
函数的性质 |
|
指数函数 |
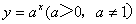 |
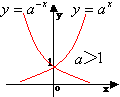 |
a):不论x为何值,y总为正数;
b):当x=0时,y=1. |
|
对数函数 |
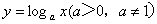 |
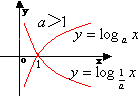 |
a):其图形总位于y轴右侧,并过(1,0)点
b):当a>1时,在区间(0,1)的值为负;在区间(-,+∞)的值为正;在定义域内单调增. |
|
幂函数 |
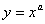 a为任意实数 a为任意实数 |
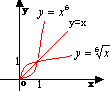 这里只画出部分函数图形的一部分。
这里只画出部分函数图形的一部分。 |
令a=m/n
a):当m为偶数n为奇数时,y是偶函数;
b):当m,n都是奇数时,y是奇函数;
c):当m奇n偶时,y在(-∞,0)无意义. |
|
三角函数 |
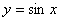 (正弦函数)
这里只写出了正弦函数 (正弦函数)
这里只写出了正弦函数 |
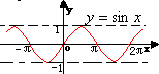 |
a):正弦函数是以2π为周期的周期函数
b):正弦函数是奇函数且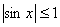 |
|
反三角函数 |
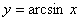 (反正弦函数)
这里只写出了反正弦函数 (反正弦函数)
这里只写出了反正弦函数 |
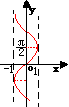 |
a):由于此函数为多值函数,因此我们此函数值限制在[-π/2,π/2]上,并称其为反正弦函数的主值. |
⑵、初等函数:由基本初等函数与常数经过有限次的有理运算及有限次的函数复合所产生并且能用一个解析式表出的函数称为初等函数.
例题: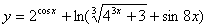 是初等函数。
是初等函数。
5、复合函数
复合函数的定义:若y是u的函数: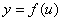 ,而u又是x的函数:
,而u又是x的函数: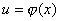 ,且
,且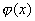 的函数值的全部或部分在
的函数值的全部或部分在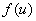 的定义域内,那末,y通过u的联系也是x的函数,我们称后一个函数是由函数
的定义域内,那末,y通过u的联系也是x的函数,我们称后一个函数是由函数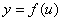 及
及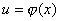 复合而成的函数,简称复合函数,记作
复合而成的函数,简称复合函数,记作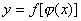 ,其中u叫做中间变量。
,其中u叫做中间变量。
注:并不是任意两个函数就能复合;复合函数还可以由更多函数构成。
例题:函数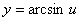 与函数
与函数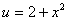 是不能复合成一个函数的。
是不能复合成一个函数的。
因为对于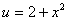 的定义域(-∞,+∞)中的任何x值所对应的u值(都大于或等于2),使
的定义域(-∞,+∞)中的任何x值所对应的u值(都大于或等于2),使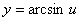 都没有定义。
都没有定义。
4、反函数
⑴、反函数的定义:设有函数 ,若变量y在函数的值域内任取一值y0时,变量x在函数的定义域内必有一值x0与之对应,即
,若变量y在函数的值域内任取一值y0时,变量x在函数的定义域内必有一值x0与之对应,即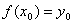 ,那末变量x是变量y的函数.这个函数用
,那末变量x是变量y的函数.这个函数用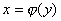 来表示,称为函数
来表示,称为函数 的反函数.
的反函数.
注:由此定义可知,函数 也是函数
也是函数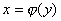 的反函数。
的反函数。
⑵、反函数的存在定理:若 在(a,b)上严格增(减),其值域为 R,则它的反函数必然在R上确定,且严格增(减).
在(a,b)上严格增(减),其值域为 R,则它的反函数必然在R上确定,且严格增(减).
注:严格增(减)即是单调增(减)
例题:y=x2,其定义域为(-∞,+∞),值域为[0,+∞).对于y取定的非负值,可求得x=±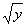 .若我们不加条件,由y的值就不能唯一确定x的值,也就是在区间(-∞,+∞)上,函数不是严格增(减),故其没有反函数。如果我们加上条件,要求x≥0,则对y≥0、x=
.若我们不加条件,由y的值就不能唯一确定x的值,也就是在区间(-∞,+∞)上,函数不是严格增(减),故其没有反函数。如果我们加上条件,要求x≥0,则对y≥0、x=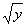 就是y=x2在要求x≥0时的反函数。即是:函数在此要求下严格增(减).
就是y=x2在要求x≥0时的反函数。即是:函数在此要求下严格增(减).
⑶、反函数的性质:在同一坐标平面内, 与
与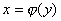 的图形是关于直线y=x对称的。
的图形是关于直线y=x对称的。
例题:函数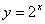 与函数
与函数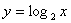 互为反函数,则它们的图形在同一直角坐标系中是关于直线y=x对称的。如右图所示:
互为反函数,则它们的图形在同一直角坐标系中是关于直线y=x对称的。如右图所示:
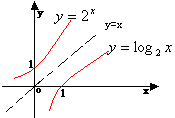
3、函数的简单性态
⑴、函数的有界性:如果对属于某一区间I的所有x值总有│f(x)│≤M成立,其中M是一个与x无关的常数,那么我们就称f(x)在区间I有界,否则便称无界。
注:一个函数,如果在其整个定义域内有界,则称为有界函数
例题:函数cosx在(-∞,+∞)内是有界的.
⑵、函数的单调性:如果函数 在区间(a,b)内随着x增大而增大,即:对于(a,b)内任意两点x1及x2,当x1<x2时,有
在区间(a,b)内随着x增大而增大,即:对于(a,b)内任意两点x1及x2,当x1<x2时,有  ,则称函数
,则称函数 在区间(a,b)内是单调增加的。如果函数
在区间(a,b)内是单调增加的。如果函数 在区间(a,b)内随着x增大而减小,即:对于(a,b)内任意两点x1及x2,当x1<x2时,有
在区间(a,b)内随着x增大而减小,即:对于(a,b)内任意两点x1及x2,当x1<x2时,有 ,则称函数
,则称函数 在区间(a,b)内是单调减小的。
在区间(a,b)内是单调减小的。
例题:函数 =x2在区间(-∞,0)上是单调减小的,在区间(0,+∞)上是单调增加的。
=x2在区间(-∞,0)上是单调减小的,在区间(0,+∞)上是单调增加的。
⑶、函数的奇偶性
如果函数 对于定义域内的任意x都满足
对于定义域内的任意x都满足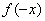 =
= ,则
,则 叫做偶函数;如果函数
叫做偶函数;如果函数 对于定义域内的任意x都满足
对于定义域内的任意x都满足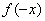 =-
=- ,则
,则 叫做奇函数。
叫做奇函数。
注:偶函数的图形关于y轴对称,奇函数的图形关于原点对称。
⑷、函数的周期性
对于函数 ,若存在一个不为零的数l,使得关系式
,若存在一个不为零的数l,使得关系式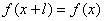 对于定义域内任何x值都成立,则
对于定义域内任何x值都成立,则 叫做周期函数,l是
叫做周期函数,l是 的周期。
的周期。
注:我们说的周期函数的周期是指最小正周期。
例题:函数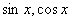 是以2π为周期的周期函数;函数tgx是以π为周期的周期函数。
是以2π为周期的周期函数;函数tgx是以π为周期的周期函数。
2、函数
⑴、函数的定义:如果当变量x在其变化范围内任意取定一个数值时,量y按照一定的法则f总有确定的数值与它对应,则称y是x的函数。变量x的变化范围叫做这个函数的定义域。通常x叫做自变量,y叫做函数值(或因变量),变量y的变化范围叫做这个函数的值域。注:为了表明y是x的函数,我们用记号y=f(x)、y=F(x)等等来表示。这里的字母"f"、"F"表示y与x之间的对应法则即函数关系,它们是可以任意采用不同的字母来表示的。如果自变量在定义域内任取一个确定的值时,函数只有一个确定的值和它对应,这种函数叫做单值函数,否则叫做多值函数。这里我们只讨论单值函数。
⑵、函数相等
由函数的定义可知,一个函数的构成要素为:定义域、对应关系和值域。由于值域是由定义域和对应关系决定的,所以,如果两个函数的定义域和对应关系完全一致,我们就称两个函数相等。
⑶、域函数的表示方法
a):解析法:用数学式子表示自变量和因变量之间的对应关系的方法即是解析法。例:直角坐标系中,半径为r、圆心在原点的圆的方程是:x2+y2=r2
b):表格法:将一系列的自变量值与对应的函数值列成表来表示函数关系的方法即是表格法。例:在实际应用中,我们经常会用到的平方表,三角函数表等都是用表格法表示的函数。
c):图示法:用坐标平面上曲线来表示函数的方法即是图示法。一般用横坐标表示自变量,纵坐标表示因变量。例:直角坐标系中,半径为r、圆心在原点的圆用图示法表示为:
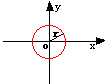
2、常量与变量
⑴、变量的定义:我们在观察某一现象的过程时,常常会遇到各种不同的量,其中有的量在过程中不起变化,我们把其称之为常量;有的量在过程中是变化的,也就是可以取不同的数值,我们则把其称之为变量。注:在过程中还有一种量,它虽然是变化的,但是它的变化相对于所研究的对象是极其微小的,我们则把它看作常量。
⑵、变量的表示:如果变量的变化是连续的,则常用区间来表示其变化范围。在数轴上来说,区间是指介于某两点之间的线段上点的全体。
|
区间的名称 |
区间的满足的不等式 |
区间的记号 |
区间在数轴上的表示 |
|
闭区间 |
a≤x≤b |
[a,b] |
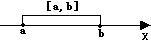 |
|
开区间 |
a<x<b |
(a,b) |
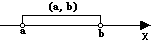 |
|
半开区间 |
a<x≤b或a≤x<b |
(a,b]或[a,b) |
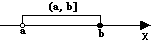
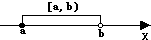 |
以上我们所述的都是有限区间,除此之外,还有无限区间:
[a,+∞):表示不小于a的实数的全体,也可记为:a≤x<+∞;
(-∞,b):表示小于b的实数的全体,也可记为:-∞<x<b;
(-∞,+∞):表示全体实数,也可记为:-∞<x<+∞
注:其中-∞和+∞,分别读作"负无穷大"和"正无穷大",它们不是数,仅仅是记号。
⑶、邻域:设α与δ是两个实数,且δ>0.满足不等式│x-α│<δ的实数x的全体称为点α的δ邻域,点α称为此邻域的中心,δ称为此邻域的半径。
5、无限集合A={1,2,3,4,…,n,…},B={2,4,6,8,…,2n,…},你能设计一种比较这两个集合中元素个数多少的方法吗?
4、对于有限集合A、B、C,能不能找出这三个集合中元素个数与交集、并集元素个数之间的关系呢?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com