
|
微分方程的基本概念 |
在许多科技领域里,常会遇到这样的问题:
某个函数是怎样的并不知道,但根据科技领域的普遍规律,却可以知道这个未知函数及其导数与自变量之间会满足某种关系。下面我们先来看一个例子:
例题:已知一条曲线过点(1,2),且在该直线上任意点P(x,y)处的切线斜率为2x,求这条曲线方程
解答:设所求曲线的方程为y=y(x),我们根据导数的几何意义,可知y=y(x)应满足方程:
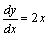 我们发现这个方程中含有未知函数y的导数。这里我们先不求解。
微分方程的概念
我们把含有未知函数的导数(或微分)的方程称为微分方程。
在一个微分方程中所出现的导数的最高阶数称为微分方程的阶。当然阶数越高的微分方程越麻烦。
从微分方程求出未知函数是什么就叫做解微分方程。满足微分方程的函数(它要在某区间上连续)称为微分方程的解,微分方程的一般形式的解称为微分方程的一般解.
满足微分方程的一个有特殊要求的解称为微分方程的一特解,这种特解通常是满足一定的附加条件的解。
通常,微分方程的一般解里,含有一些任意常数,其个数与微分方程的阶数相同,因此用来确定任意常数以从一般解得出一个特解的附加条件的个数也与微分方程的阶数相同. 我们发现这个方程中含有未知函数y的导数。这里我们先不求解。
微分方程的概念
我们把含有未知函数的导数(或微分)的方程称为微分方程。
在一个微分方程中所出现的导数的最高阶数称为微分方程的阶。当然阶数越高的微分方程越麻烦。
从微分方程求出未知函数是什么就叫做解微分方程。满足微分方程的函数(它要在某区间上连续)称为微分方程的解,微分方程的一般形式的解称为微分方程的一般解.
满足微分方程的一个有特殊要求的解称为微分方程的一特解,这种特解通常是满足一定的附加条件的解。
通常,微分方程的一般解里,含有一些任意常数,其个数与微分方程的阶数相同,因此用来确定任意常数以从一般解得出一个特解的附加条件的个数也与微分方程的阶数相同. |
|
可分离变量的微分方程与齐次方程 |
下面我们来学习用积分法解一阶微分方程的问题。
并不是所有的一阶微分方程都可以用积分法求解,只有一些特殊形式的一阶微分方程可以用积分法求解,并且解法也各不相同。因此,我们学习时要认清各种微分方程的特点及它们的解法。
可分离变量的微分方程
这种方程的形式为: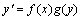 我们往往会以为将上式两端积分即可求解。其实是不对的。因为两端积分后,得
我们往往会以为将上式两端积分即可求解。其实是不对的。因为两端积分后,得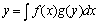 ,右端是什么也求不出的,所以求不出y来。
其正确解法为:设y=y(x)为所求的解,于是当y=y(x)时,有 ,右端是什么也求不出的,所以求不出y来。
其正确解法为:设y=y(x)为所求的解,于是当y=y(x)时,有
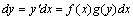 ,即 ,即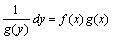 这一步把y的函数及dy与x的函数及dx分开了,称为分离变量,这是求解的关键的一步,下一步我们就可由不定积分换元法进行求解了。
例题:求方程
这一步把y的函数及dy与x的函数及dx分开了,称为分离变量,这是求解的关键的一步,下一步我们就可由不定积分换元法进行求解了。
例题:求方程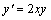 的通解。
解答:这是一个可分离变量的方程,分离变量后得 的通解。
解答:这是一个可分离变量的方程,分离变量后得
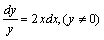 两端分别积分,得
两端分别积分,得
 令
令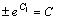 ,得 ,得
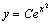 这就是该方程的通解。
齐次微分方程
这种微分方程的形式为:
这就是该方程的通解。
齐次微分方程
这种微分方程的形式为: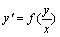 它也不能由两端积分求解。其求解步骤为:
令
它也不能由两端积分求解。其求解步骤为:
令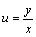 ,则 ,则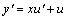 ,y的微分方程就化成了u的微分方程 ,y的微分方程就化成了u的微分方程
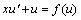 即:
即: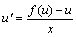 这就化成了可分离变量的微分方程,再由上面我们所学的方法就可求出方程的通解。
例题:求方程
这就化成了可分离变量的微分方程,再由上面我们所学的方法就可求出方程的通解。
例题:求方程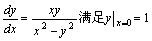 的特解。
解答:这是一个齐次方程。令y=ux代入,得 的特解。
解答:这是一个齐次方程。令y=ux代入,得
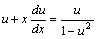 分离变量后,得
分离变量后,得
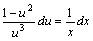 两端分别积分,得
两端分别积分,得
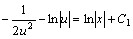 或
或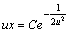 其中
其中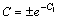 代回u=y/x,得原方程的通解为
代回u=y/x,得原方程的通解为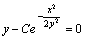 将初始条件y(0)=1代入,得 C=1.
所以满足初始条件的特解为
将初始条件y(0)=1代入,得 C=1.
所以满足初始条件的特解为
|
|
线性微分方程 |
线性微分方程
这种微分方程的形式为: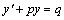 ,其中,p,q与y,y'无关,但可以与x有关.它对y与y'而言是一次的,故被称之为一阶线性微分方程。
当q=0时称为齐次线性微分方程;当q≠0时称为非齐次线性微分方程。
齐次线性微分方程的解法
齐次线性微分方程的形式为: ,其中,p,q与y,y'无关,但可以与x有关.它对y与y'而言是一次的,故被称之为一阶线性微分方程。
当q=0时称为齐次线性微分方程;当q≠0时称为非齐次线性微分方程。
齐次线性微分方程的解法
齐次线性微分方程的形式为: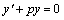 此方程是可分离变量的微分方程,分离变量后,得:
此方程是可分离变量的微分方程,分离变量后,得: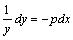 ,这就可以由我们前面所学的方法进行求解。
例题:求 ,这就可以由我们前面所学的方法进行求解。
例题:求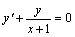 的一般解。
解答:由此方程可得 的一般解。
解答:由此方程可得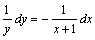 ,故 ,故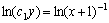 因此该方程的一般解为:
因此该方程的一般解为: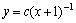 非齐次线性微分方程的解法
非齐次线性微分方程的形式为:
非齐次线性微分方程的解法
非齐次线性微分方程的形式为: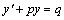 这种方程的解法为:先求出其对应的齐次线性微分方程
这种方程的解法为:先求出其对应的齐次线性微分方程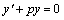 的一般解 的一般解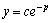 ,然后把c看作x的函数,再代到非齐次线性微分方程中来决定c,使它能满足非齐次微分方程。 ,然后把c看作x的函数,再代到非齐次线性微分方程中来决定c,使它能满足非齐次微分方程。
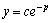 中把c作为x的函数求导数比c作为常数求导数要多处一项: 中把c作为x的函数求导数比c作为常数求导数要多处一项: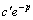 ,所以 ,所以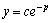 中c作为x的函数代入微分方程就得到 中c作为x的函数代入微分方程就得到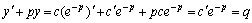 .
所以只要 .
所以只要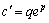 ,即 ,即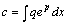 就可使非齐次线性微分方程得到满足,即 就可使非齐次线性微分方程得到满足,即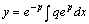 为所求的一般解。
上面我们说学的这种解法被称为Lagrange常数变易法。
例题:求解 为所求的一般解。
上面我们说学的这种解法被称为Lagrange常数变易法。
例题:求解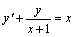 解答:相应齐次线性微分方程
解答:相应齐次线性微分方程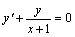 的一般解为: 的一般解为: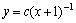 把c看成x的函数代入得:
把c看成x的函数代入得: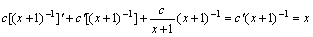 因此:c'=x(x+1)
∴
因此:c'=x(x+1)
∴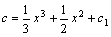 故:
故: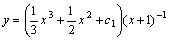 就是非齐次线性微分方程的一般解。 就是非齐次线性微分方程的一般解。 |
|
可降阶的高阶方程 |
求解高阶微分方程的方法之一是设法降低方程的阶数。下面我们以二阶方程为例来学习三种可以降阶的方程。
1.右端仅含x的方程:y"=f(x)
对这类方程,只须两端分别积分一次就可化为一阶方程
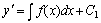 ,
再次积分,即可求出方程得通解。 ,
再次积分,即可求出方程得通解。
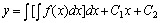 例题:求方程y"=cosx的通解。
解答:一次积分得:
例题:求方程y"=cosx的通解。
解答:一次积分得:
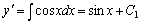 二次积分即得到方程得通解:
二次积分即得到方程得通解:
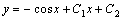 2.右端不显含y的方程:y"=f(x,y')
我们为了把方程降阶,可令y'=p,将p看作是新的未知函数,x仍是自变量,于是
2.右端不显含y的方程:y"=f(x,y')
我们为了把方程降阶,可令y'=p,将p看作是新的未知函数,x仍是自变量,于是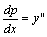 ,代入原方程得: ,代入原方程得:
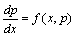 这就是一个一阶方程,然后即可由我们前面学的方法进行求解了。
例题:求方程
这就是一个一阶方程,然后即可由我们前面学的方法进行求解了。
例题:求方程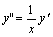 的通解。
解答:令y'=p. 的通解。
解答:令y'=p.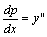 ,代入方程,得 ,代入方程,得
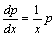 分离变量后,得
分离变量后,得
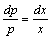 积分,得
积分,得
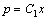 .即 .即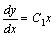 再积分,即得原方程的通解:
再积分,即得原方程的通解:
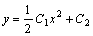 .
3.右端不显含x的方程:y"=f(y,y')
我们为了把方程降阶,可令y'=p,将p看作是自变量y的函数,有 .
3.右端不显含x的方程:y"=f(y,y')
我们为了把方程降阶,可令y'=p,将p看作是自变量y的函数,有
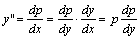 代入原方程,得
代入原方程,得
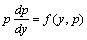 这是关于p的一阶方程,我们可由此解出通解,然后再代入原方程求解,即可。
例题:求方程
这是关于p的一阶方程,我们可由此解出通解,然后再代入原方程求解,即可。
例题:求方程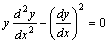 的通解
解答:令 的通解
解答:令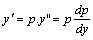 代入原方程得: 代入原方程得:
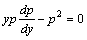 它相当于两个方程:
它相当于两个方程:
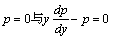 由第一个方程解得:y=C;
第二个方程可用分离变量法解得
p =C1y
从而
由第一个方程解得:y=C;
第二个方程可用分离变量法解得
p =C1y
从而
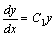 由此再分离变量,解得:
由此再分离变量,解得:
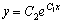 这就是原方程的通解(解y=C包含在这个解中)
这就是原方程的通解(解y=C包含在这个解中) |
|
线性微分方程解的结构 |
我们以二阶方程为例来说明线性方程解的结构,当然这些结论也适合于高阶线性微分方程。
二阶线性方程的一般形式为
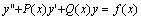 其中y",y',y都是一次的,否则称为二阶非线性方程。
线性齐次方程解的结构
二阶线性齐次方程的形式为:
其中y",y',y都是一次的,否则称为二阶非线性方程。
线性齐次方程解的结构
二阶线性齐次方程的形式为:
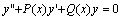 定理:如果函数
定理:如果函数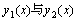 均是方程 均是方程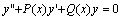 的解,那末 的解,那末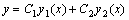 也是该方程的解,其中C1,C2为任意常数。
线性齐次方程的这一性质,又称为解的叠和性。
问题:我们所求得的解 也是该方程的解,其中C1,C2为任意常数。
线性齐次方程的这一性质,又称为解的叠和性。
问题:我们所求得的解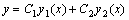 是不是方程的 是不是方程的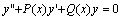 通解呢?
一般来说,这是不一定的,那么什么情况下它才是方程的通解呢?为此我们由引出了两个概念:线性相关与线性独立。
定义:设 通解呢?
一般来说,这是不一定的,那么什么情况下它才是方程的通解呢?为此我们由引出了两个概念:线性相关与线性独立。
定义:设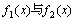 是定义在区间I的两个函数,如果 是定义在区间I的两个函数,如果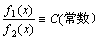 ,那末称此两函数在区间I线性相关,否则,即 ,那末称此两函数在区间I线性相关,否则,即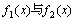 之比不恒等于一个常数,那末称此两函数线性独立或线性无关。
为此我们有了关于线性齐次方程特解的定理。
定理:如果 之比不恒等于一个常数,那末称此两函数线性独立或线性无关。
为此我们有了关于线性齐次方程特解的定理。
定理:如果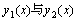 是二阶线线性齐次方程的任意两个线性独立的特解,那末 是二阶线线性齐次方程的任意两个线性独立的特解,那末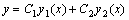 就是该方程的通解,其中C1,C2为任意常数。
线性非齐次方程解的结构
二阶线性非齐次方程的形式为: 就是该方程的通解,其中C1,C2为任意常数。
线性非齐次方程解的结构
二阶线性非齐次方程的形式为:
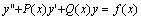 对于一阶线性非齐次方程我们知道,线性非齐次方程的通解等于它的一个特解与对应的齐次方程通解之和。那末这个结论对高阶线性非齐次方程适合吗?
答案是肯定的。为此我们有下面的定理。
定理:设y是二阶线性非齐次方程
对于一阶线性非齐次方程我们知道,线性非齐次方程的通解等于它的一个特解与对应的齐次方程通解之和。那末这个结论对高阶线性非齐次方程适合吗?
答案是肯定的。为此我们有下面的定理。
定理:设y是二阶线性非齐次方程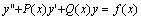 的任一特解,Y是与该方程对应的齐次线性方程的通解,那末 y=y+Y 就是方程 的任一特解,Y是与该方程对应的齐次线性方程的通解,那末 y=y+Y 就是方程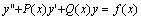 的通解。
我们为了以后的解题方便,又给出了一个定理,如下:
定理:设有线性非齐次方程 的通解。
我们为了以后的解题方便,又给出了一个定理,如下:
定理:设有线性非齐次方程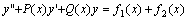 .如果 .如果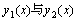 分别是方程 分别是方程
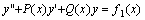 与方程 与方程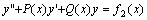 的解,那末
的解,那末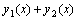 就是原方程的解。 就是原方程的解。 |
|
二阶常系数齐次线性方程的解法 |
前面我们已经知道了,无论是线性齐次方程和非齐次方程,它们的通解结构虽然知道,但通解的寻求却是建立在已知特解的基础上。但是,即使对二阶线性齐次方程,特解的寻求也没有一般的方法。但是对于常系数的二阶线性齐次方程,它的通解可按一定的方法很容易求的。
二阶线性齐次方程的解法
二阶线性齐次方程的一般形式为: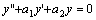 ,其中a1,a2为实常数。
我们知道指数函数eax求导后仍为指数函数。利用这个性质,可适当的选择常数ρ,使eax满足方程上面的方程。我们可令: ,其中a1,a2为实常数。
我们知道指数函数eax求导后仍为指数函数。利用这个性质,可适当的选择常数ρ,使eax满足方程上面的方程。我们可令: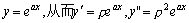 ,代入上面的方程得: ,代入上面的方程得:
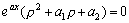 因为eax≠0,所以:
因为eax≠0,所以:
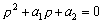 这样,对于上面二次方程的每个根ρ,eax就是方程
这样,对于上面二次方程的每个根ρ,eax就是方程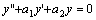 的一个解。方程 的一个解。方程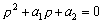 就被称为方程 就被称为方程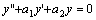 的特征方程。根据这个代数方程的根的不同性质,我们分三种不同的情况来讨论:
1.特征方程有两个不等的实根的情形
设此两实根为 的特征方程。根据这个代数方程的根的不同性质,我们分三种不同的情况来讨论:
1.特征方程有两个不等的实根的情形
设此两实根为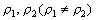 。于是 。于是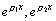 是齐次方程 是齐次方程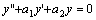 的两个特解,由于它们之比不等于常数,所以它们线性独立,因此,方程 的两个特解,由于它们之比不等于常数,所以它们线性独立,因此,方程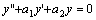 的通解为: 的通解为:
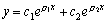 其中c1,c2为实常数。
2.特征方程有重根的情形
此时特征方程的重根应为:
其中c1,c2为实常数。
2.特征方程有重根的情形
此时特征方程的重根应为: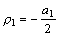 ,于是只能得到 ,于是只能得到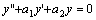 的一个特解: 的一个特解: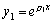 ,我们可根据常数变易法再求其另一个特解为: ,我们可根据常数变易法再求其另一个特解为: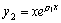 .于是方程 .于是方程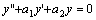 的通解为: 的通解为:
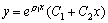 3.特征方程有共轭复根的情形
设共轭复根为
3.特征方程有共轭复根的情形
设共轭复根为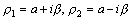 ,那末 ,那末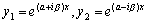 是方程 是方程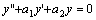 的两个线性独立的解,但是这种复数形式的解使用不方便,为了得到实数形式的解,利用欧拉公式: 的两个线性独立的解,但是这种复数形式的解使用不方便,为了得到实数形式的解,利用欧拉公式: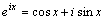 ,为此可以得到方程 ,为此可以得到方程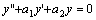 的通解: 的通解:
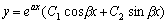 由上面可知,求二阶常系数线性齐次方程通解的步骤为:
1.对照方程
由上面可知,求二阶常系数线性齐次方程通解的步骤为:
1.对照方程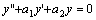 写出其特征方程: 写出其特征方程: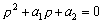 ;
2.求出特征方程的两个根:ρ1,ρ2
3.根据ρ1,ρ2是不同实根,相同实根,共轭复根,分别利用上面的公式写出原方程的通解。
例题:求方程 ;
2.求出特征方程的两个根:ρ1,ρ2
3.根据ρ1,ρ2是不同实根,相同实根,共轭复根,分别利用上面的公式写出原方程的通解。
例题:求方程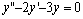 的通解.
解答:此方程的特征方程为: 的通解.
解答:此方程的特征方程为:
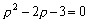 它有两个不相同的实根
它有两个不相同的实根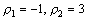 ,因此所求的通解为: ,因此所求的通解为:
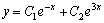 |
|
二阶常系数非齐次线性方程的解法 |
我们来学习二阶常系数线性非齐次方程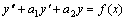 的求解方法.由前面我们知道线性非齐次方程的通解,等于它的任一特解与对应齐次方程的通解之和。前面我们已知道对应齐次方程的通解的解法,现在的关键是怎样求得特解。
二阶常系数非齐次线性方程的解法
常系数二阶线性非齐次方程的一般形式为: 的求解方法.由前面我们知道线性非齐次方程的通解,等于它的任一特解与对应齐次方程的通解之和。前面我们已知道对应齐次方程的通解的解法,现在的关键是怎样求得特解。
二阶常系数非齐次线性方程的解法
常系数二阶线性非齐次方程的一般形式为:
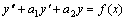 下面我们根据f(x)具有下列特殊情形时,来给出求其特解的公式:
(1):设
下面我们根据f(x)具有下列特殊情形时,来给出求其特解的公式:
(1):设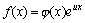 ,其中μ为一常数,
若 ,其中μ为一常数,
若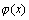 为零次多项式,此时:
a):当μ不是特征方程的根时,可设 为零次多项式,此时:
a):当μ不是特征方程的根时,可设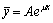 b):当μ是特征方程的单根时,可设
b):当μ是特征方程的单根时,可设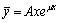 c):当μ是特征方程的重根时,可设
c):当μ是特征方程的重根时,可设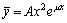 若
若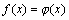 为一m次多项式,即:μ=0,此时
a):当a2≠0即μ=0不是特征方程的根时,可设 为一m次多项式,即:μ=0,此时
a):当a2≠0即μ=0不是特征方程的根时,可设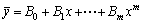 b):当a2=0,a1≠0时,即μ=0是特征方程的单根时,可设
b):当a2=0,a1≠0时,即μ=0是特征方程的单根时,可设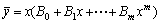 c):当a2=0,a1=0时,即μ=0是特征方程的重根时,可设
c):当a2=0,a1=0时,即μ=0是特征方程的重根时,可设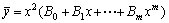 例题:求方程
例题:求方程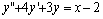 的一个特解
解答:对应的特征方程为 的一个特解
解答:对应的特征方程为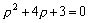 原方程右端不出现
原方程右端不出现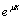 ,但可以把它看作是 ,但可以把它看作是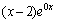 ,即μ=0
因为μ=0不是特征方程的根,所以设特解为 ,即μ=0
因为μ=0不是特征方程的根,所以设特解为
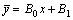 代入原方程,得
代入原方程,得
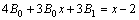 于是:
于是:
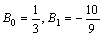 故所求的特解为:
故所求的特解为:
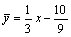 (2):设
(2):设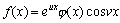 或 或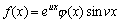 ,其中a,μ,v为常数。
此时的特解为: ,其中a,μ,v为常数。
此时的特解为: 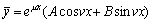 例题:求方程
例题:求方程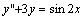 的特解
解答:显然可设特解为: 的特解
解答:显然可设特解为:
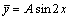 代入原方程得:
代入原方程得:
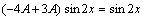 由此得:
A=-1
从而原方程的特解是
由此得:
A=-1
从而原方程的特解是
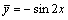 |
|
二重积分的概念及性质 |
前面我们已经知道了,定积分与曲边梯形的面积有关。下面我们通过曲顶柱体的体积来引出二重积分的概念,在此我们不作详述,请大家参考有关书籍。
二重积分的定义
设z=f(x,y)为有界闭区域(σ)上的有界函数:
(1)把区域(σ)任意划分成n个子域(△σk)(k=1,2,3,…,n),其面积记作△σk(k=1,2,3,…,n);
(2)在每一个子域(△σk)上任取一点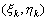 ,作乘积 ,作乘积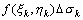 ;
(3)把所有这些乘积相加,即作出和数 ;
(3)把所有这些乘积相加,即作出和数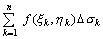 (4)记子域的最大直径d.如果不论子域怎样划分以及
(4)记子域的最大直径d.如果不论子域怎样划分以及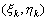 怎样选取,上述和数当n→+∞且d→0时的极限存在,那末称此极限为函数f(x,y)在区域(σ)上的二重积分.记作: 怎样选取,上述和数当n→+∞且d→0时的极限存在,那末称此极限为函数f(x,y)在区域(σ)上的二重积分.记作: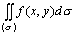 即:
即: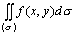 = =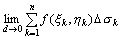 其中x与y称为积分变量,函数f(x,y)称为被积函数,f(x,y)dσ称为被积表达式,(σ)称为积分区域.
关于二重积分的问题
对于二重积分的定义,我们并没有f(x,y)≥0的限.容易看出,当f(x,y)≥0时,二重积分
其中x与y称为积分变量,函数f(x,y)称为被积函数,f(x,y)dσ称为被积表达式,(σ)称为积分区域.
关于二重积分的问题
对于二重积分的定义,我们并没有f(x,y)≥0的限.容易看出,当f(x,y)≥0时,二重积分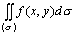 在几何上就是以z=f(x,y)为曲顶,以(σ)为底且母线平行于z轴的曲顶柱体的体积。
上述就是二重积分的几何意义。
如果被积函数f(x,y)在积分区域(σ)上连续,那末二重积分 在几何上就是以z=f(x,y)为曲顶,以(σ)为底且母线平行于z轴的曲顶柱体的体积。
上述就是二重积分的几何意义。
如果被积函数f(x,y)在积分区域(σ)上连续,那末二重积分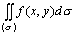 必定存在。
二重积分的性质
(1).被积函数中的常数因子可以提到二重积分符号外面去. 必定存在。
二重积分的性质
(1).被积函数中的常数因子可以提到二重积分符号外面去.
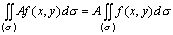 (2).有限个函数代数和的二重积分等于各函数二重积分的代数和.
(2).有限个函数代数和的二重积分等于各函数二重积分的代数和.
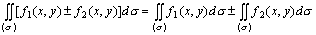 (3).如果把积分区域(σ)分成两个子域(σ1)与(σ2),即(σ)=(σ1)+(σ2),那末:
(3).如果把积分区域(σ)分成两个子域(σ1)与(σ2),即(σ)=(σ1)+(σ2),那末:
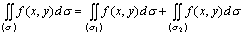 (4).如果在(σ)上有f(x,y)≤g(x,y),那末:
(4).如果在(σ)上有f(x,y)≤g(x,y),那末:
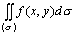 ≤ ≤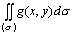 (5).设f(x,y)在闭域(σ)上连续,则在(σ)上至少存在一点(ξ,η),使
(5).设f(x,y)在闭域(σ)上连续,则在(σ)上至少存在一点(ξ,η),使
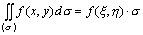 其中σ是区域(σ)的面积.
其中σ是区域(σ)的面积. |
|
二重积分的计算法 |
直角坐标系中的计算方法
这里我们采取的方法是累次积分法。也就是先把x看成常量,对y进行积分,然后在对x进行积分,或者是先把y看成常量,对x进行积分,然后在对y进行积分。为此我们有积分公式,如下:
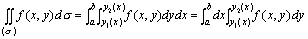 或
或 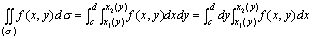 在这里我们可能会有这个问题:累次积分的上下限是怎么确定的呢?
累次积分上下限的确定方法
我们先来对区域作些补充说明:如果经过区域(σ)内任意一点(即不是区域边界上的点)作平行于y轴(或x轴)的直线,且此直线交(σ)的边界不超过两点,那末称(σ)为沿y轴(x轴)方向的正规区域.如果(σ)即是沿y轴方向也是沿x轴方向的正规区域,那末(σ)就称为正规区域.下图所示的即为正规区域:
在这里我们可能会有这个问题:累次积分的上下限是怎么确定的呢?
累次积分上下限的确定方法
我们先来对区域作些补充说明:如果经过区域(σ)内任意一点(即不是区域边界上的点)作平行于y轴(或x轴)的直线,且此直线交(σ)的边界不超过两点,那末称(σ)为沿y轴(x轴)方向的正规区域.如果(σ)即是沿y轴方向也是沿x轴方向的正规区域,那末(σ)就称为正规区域.下图所示的即为正规区域:
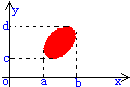 关于累次积分上下限的取法如下所述:
(1).如果(σ)为沿y轴方向的正规区域,那末二重积分可化为先对y再对x的累次积分.其中对y的积分下限是(σ)的下部边界曲线所对应的函数y1(x),积分上限是上部边界曲线所对应的函数y2(x).对x的积分下限与上限分别是(σ)的最左与最右点的横坐标a与b.
(2).如果(σ)为沿x轴方向的正规区域,那末二重积分可化为先对x再对y的累次积分.其中对x的积分下限是(σ)的左部边界曲线所对应的函数x1(y),积分上限是右部边界曲线所对应的函数x2(y).对y的积分下限与上限分别是(σ)的最低与最高点的横坐标c与d.
(3).如果(σ)为正规区域,那末累次积分可以交换积分次序。
(4).如果(σ)既不是沿y轴方向的正规区域,也不是沿x轴方向的正规区域,那末总可以把它化分成几块沿y轴方向的正规区域或沿x轴方向的正规区域,然后根据积分的性质即可求解积分.
例题:求二重积分
关于累次积分上下限的取法如下所述:
(1).如果(σ)为沿y轴方向的正规区域,那末二重积分可化为先对y再对x的累次积分.其中对y的积分下限是(σ)的下部边界曲线所对应的函数y1(x),积分上限是上部边界曲线所对应的函数y2(x).对x的积分下限与上限分别是(σ)的最左与最右点的横坐标a与b.
(2).如果(σ)为沿x轴方向的正规区域,那末二重积分可化为先对x再对y的累次积分.其中对x的积分下限是(σ)的左部边界曲线所对应的函数x1(y),积分上限是右部边界曲线所对应的函数x2(y).对y的积分下限与上限分别是(σ)的最低与最高点的横坐标c与d.
(3).如果(σ)为正规区域,那末累次积分可以交换积分次序。
(4).如果(σ)既不是沿y轴方向的正规区域,也不是沿x轴方向的正规区域,那末总可以把它化分成几块沿y轴方向的正规区域或沿x轴方向的正规区域,然后根据积分的性质即可求解积分.
例题:求二重积分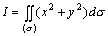 ,其中(σ)是由 ,其中(σ)是由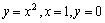 所围成的区域。
解答:因为是正规区域,所以我们可先对y后对x积分,也可先对x后对y积分。这里我们采用前者
先对y后对x积分: 所围成的区域。
解答:因为是正规区域,所以我们可先对y后对x积分,也可先对x后对y积分。这里我们采用前者
先对y后对x积分:
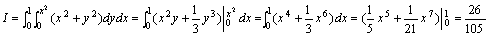 极坐标系中的计算法
如果二重积分的被积函数和积分区域(σ)的边界方程均由极坐标的形式给出,那末我们如何计算呢?下面我们给出极坐标系中二重积分的计算公式.
如果极点O在(σ)的外部,区域(σ)用不等式表示为R1(θ)≤ρ≤R2(θ),α≤θ≤β,则积分公式如下:
极坐标系中的计算法
如果二重积分的被积函数和积分区域(σ)的边界方程均由极坐标的形式给出,那末我们如何计算呢?下面我们给出极坐标系中二重积分的计算公式.
如果极点O在(σ)的外部,区域(σ)用不等式表示为R1(θ)≤ρ≤R2(θ),α≤θ≤β,则积分公式如下:
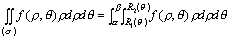 如果极点O在(σ)的内部,区域(σ)的边界方程为ρ=R(θ),0≤θ≤2π,则积分公式如下:
如果极点O在(σ)的内部,区域(σ)的边界方程为ρ=R(θ),0≤θ≤2π,则积分公式如下:
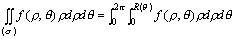 如果极点O在(σ)的边界上,边界方程为ρ=R(θ),θ1≤θ≤θ2,则积分公式如下:
如果极点O在(σ)的边界上,边界方程为ρ=R(θ),θ1≤θ≤θ2,则积分公式如下:
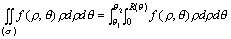 有了上面这些公式,一些在直角坐标系中不易积出而在极坐标系中易积出的函数,我们就可以把它转化为在极坐标系中的积分即可,反之依然。
注:直角坐标与极坐标的转换公式为:
有了上面这些公式,一些在直角坐标系中不易积出而在极坐标系中易积出的函数,我们就可以把它转化为在极坐标系中的积分即可,反之依然。
注:直角坐标与极坐标的转换公式为:
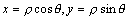 例题:求
例题:求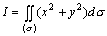 ,其中(σ)是圆环a2≤x2+y2≤b2
解答:由于积分域由同心圆围成以及被积函数的形式,显然,这个二重积分化为极坐标计算比较方便。
把 ,其中(σ)是圆环a2≤x2+y2≤b2
解答:由于积分域由同心圆围成以及被积函数的形式,显然,这个二重积分化为极坐标计算比较方便。
把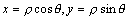 ,dσ=ρdρdθ代入,即可转化为极坐标系的积分形式。如下: ,dσ=ρdρdθ代入,即可转化为极坐标系的积分形式。如下:
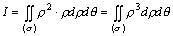 在对其进行累次积分计算:
在对其进行累次积分计算:
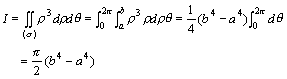 |
|
三重积分及其计算法 |
二重积分的被积函数是一个二元函数,它的积分域是-平面区域.如果考虑三元函数f(x,y,z)在一空间区域(V)上的积分,就可得到三重积分的概念。
三重积分的概念
设函数u=f(x,y,z)在空间有界闭区域(V)任意划分成n个子域(△V1),(△V2),(△V3),…,(△Vn),它们的体积分别记作△Vk(k=1,2,…,n).在每一个子域上任取一点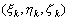 ,并作和数 ,并作和数
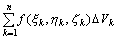 如果不论△Vk怎样划分,点
如果不论△Vk怎样划分,点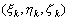 怎样选取,当n→+∞而且最大的子域直径δ→0时,这个和数的极限都存在,那末此极限就称为函数 怎样选取,当n→+∞而且最大的子域直径δ→0时,这个和数的极限都存在,那末此极限就称为函数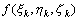 在域(V)上的三重积分,记作: 在域(V)上的三重积分,记作:
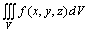 即:
即:
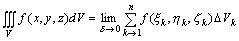 如果f(x,y,z)在域(V)上连续,那末此三重积分一定存在。
对于三重积分没有直观的几何意义,但它却有着各种不同的物理意义。
直角坐标系中三重积分的计算方法
这里我们直接给出三重积分的计算公式,具体它是怎样得来的,请大家参照有关书籍。
直角坐标系中三重积分的计算公式为:
如果f(x,y,z)在域(V)上连续,那末此三重积分一定存在。
对于三重积分没有直观的几何意义,但它却有着各种不同的物理意义。
直角坐标系中三重积分的计算方法
这里我们直接给出三重积分的计算公式,具体它是怎样得来的,请大家参照有关书籍。
直角坐标系中三重积分的计算公式为:
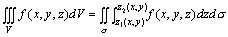 此公式是把一个三重积分转化为一个定积分与一个二重积分的问题,根据我们前面所学的结论即可求出。
例题:求
此公式是把一个三重积分转化为一个定积分与一个二重积分的问题,根据我们前面所学的结论即可求出。
例题:求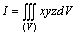 ,其中(V)是由平面x=0,y=0,z=0及x+y+z=1所围成的区域.
解答:把I化为先对z积分,再对y和x积分的累次积分,那末应把(V)投影到xOy平面上,求出投影域(σ),它就是
平面x+y+z=1与xOy平面的交线和x轴、y轴所围成的三角区域.
我们为了确定出对z积分限,在(σ)固定点(x,y),通过此点作一条平行于z的直线,它与(V)上下边界的交
点的竖坐标:z=0与z=1-x-y,这就是对z积分的下限与上限,于是由积分公式得: ,其中(V)是由平面x=0,y=0,z=0及x+y+z=1所围成的区域.
解答:把I化为先对z积分,再对y和x积分的累次积分,那末应把(V)投影到xOy平面上,求出投影域(σ),它就是
平面x+y+z=1与xOy平面的交线和x轴、y轴所围成的三角区域.
我们为了确定出对z积分限,在(σ)固定点(x,y),通过此点作一条平行于z的直线,它与(V)上下边界的交
点的竖坐标:z=0与z=1-x-y,这就是对z积分的下限与上限,于是由积分公式得:
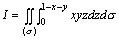 其中(σ)为平面区域:x≥0,y≥0,x+y≤1,如下图红色阴影部分所示:
其中(σ)为平面区域:x≥0,y≥0,x+y≤1,如下图红色阴影部分所示:
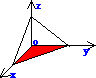 再把(σ)域上的二重积分化成先对y后对x的累次积分,得:
再把(σ)域上的二重积分化成先对y后对x的累次积分,得:
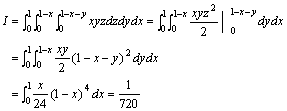 柱面坐标系中三重积分的计算法
我们先来学习一下空间中的点用极坐标的表示方法。
平面上点P可以用极坐标(ρ,θ)来确定,因此空间中的点P可用数组(ρ,θ,z)来表示.显然,空间的点P与数组(ρ,θ,z)之间的对应关系是一一对应关系,数组(ρ,θ,z)称为空间点P的柱面坐标.它与直角坐标的关系为:
柱面坐标系中三重积分的计算法
我们先来学习一下空间中的点用极坐标的表示方法。
平面上点P可以用极坐标(ρ,θ)来确定,因此空间中的点P可用数组(ρ,θ,z)来表示.显然,空间的点P与数组(ρ,θ,z)之间的对应关系是一一对应关系,数组(ρ,θ,z)称为空间点P的柱面坐标.它与直角坐标的关系为:
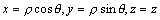 构成柱面坐标系的三族坐标面分别为:
ρ=常数:以z轴为对称轴的同轴圆柱面族,
θ=常数:通过z轴的半平面族,
z =常数:与z轴垂直的平面族.
因此,每三个这样的坐标面确定着空间的唯一的一点,由于利用了圆柱面,所以称为柱面坐标。
柱面坐标系下三重积分的计算公式为:
构成柱面坐标系的三族坐标面分别为:
ρ=常数:以z轴为对称轴的同轴圆柱面族,
θ=常数:通过z轴的半平面族,
z =常数:与z轴垂直的平面族.
因此,每三个这样的坐标面确定着空间的唯一的一点,由于利用了圆柱面,所以称为柱面坐标。
柱面坐标系下三重积分的计算公式为:
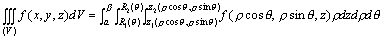 此处我们不在举例。
此处我们不在举例。 |
|
多元函数的概念 |
|||||||||
我们前面所学的函数的自变量的个数都是一个,但是在实际问题中,所涉及的函数的自变量的个数往往是两个,或者更多。
例:一个圆柱体的体积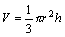 与两个独立变量r,h有关。`
我们先以二个独立的变量为基础,来给出二元函数的定义。
二元函数的定义
设有两个独立的变量x与y在其给定的变域中D中,任取一组数值时,第三个变量z就以某一确定的法则有唯一确定的值与其对应,那末变量z称为变量x与y的二元函数。
记作:z=f(x,y). 其中x与y称为自变量,函数z也叫做因变量,自变量x与y的变域D称为函数的定义域。
关于二元函数的定义域的问题
我们知道一元函数的定义域一般来说是一个或几个区间.二元函数的定义域通常是由平面上一条或几段光滑曲线所围成的连通的部分平面.这样的部分在平面称为区域.围成区域的曲线称为区域的边界,边界上的点称为边界点,包括边界在内的区域称为闭域,不包括边界在内的区域称为开域。
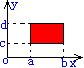
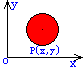
如果一个区域D(开域或闭域)中任意两点之间的距离都不超过某一常数M,则称D为有界区域;否则称D为无界区域。常见的区域有矩形域和圆形域。如下图所示: 与两个独立变量r,h有关。`
我们先以二个独立的变量为基础,来给出二元函数的定义。
二元函数的定义
设有两个独立的变量x与y在其给定的变域中D中,任取一组数值时,第三个变量z就以某一确定的法则有唯一确定的值与其对应,那末变量z称为变量x与y的二元函数。
记作:z=f(x,y). 其中x与y称为自变量,函数z也叫做因变量,自变量x与y的变域D称为函数的定义域。
关于二元函数的定义域的问题
我们知道一元函数的定义域一般来说是一个或几个区间.二元函数的定义域通常是由平面上一条或几段光滑曲线所围成的连通的部分平面.这样的部分在平面称为区域.围成区域的曲线称为区域的边界,边界上的点称为边界点,包括边界在内的区域称为闭域,不包括边界在内的区域称为开域。
如果一个区域D(开域或闭域)中任意两点之间的距离都不超过某一常数M,则称D为有界区域;否则称D为无界区域。常见的区域有矩形域和圆形域。如下图所示:
 例题:求
例题:求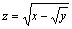 的定义域.
解答:该函数的定义域为:x≥ 的定义域.
解答:该函数的定义域为:x≥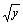 ,y≥0.
二元函数的几何表示
把自变量x、y及因变量z当作空间点的直角坐标,先在xOy平面内作出函数z=f(x,y)的定义域D;再过D域中得任一点M(x,y)作垂直于xOy平面的有向线段MP,使其值为与(x,y)对应的函数值z;
当M点在D中变动时,对应的P点的轨迹就是函数z=f(x,y)的几何图形.它通常是一张曲面,
其定义域D就是此曲面在xOy平面上的投影。 ,y≥0.
二元函数的几何表示
把自变量x、y及因变量z当作空间点的直角坐标,先在xOy平面内作出函数z=f(x,y)的定义域D;再过D域中得任一点M(x,y)作垂直于xOy平面的有向线段MP,使其值为与(x,y)对应的函数值z;
当M点在D中变动时,对应的P点的轨迹就是函数z=f(x,y)的几何图形.它通常是一张曲面,
其定义域D就是此曲面在xOy平面上的投影。 |
|||||||||
|
二元函数的极限及其连续性 |
|||||||||
在一元函数中,我们曾学习过当自变量趋向于有限值时函数的极限。对于二元函数z=f(x,y)我们同样可以学习当自变量x与y趋向于有限值ξ与η时,函数z的变化状态。
在平面xOy上,(x,y)趋向(ξ,η)的方式可以时多种多样的,因此二元函数的情况要比一元函数复杂得多。如果当点(x,y)以任意方式趋向点(ξ,η)时,f(x,y)总是趋向于一个确定的常数A,
那末就称A是二元函数f(x,y)当(x,y)→(ξ,η)时的极限。
这种极限通常称为二重极限。
下面我们用ε-δ语言给出二重极限的严格定义:
二重极限的定义
如果定义于(ξ,η)的某一去心邻域的一个二元函数f(x,y)跟一个确定的常数A有如下关系:对于任意给定的正数ε,无论怎样小,相应的必有另一个正数δ,凡是满足
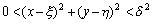 的一切(x,y)都使不等式
的一切(x,y)都使不等式
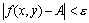 成立,
那末常数A称为函数f(x,y)当(x,y)→(ξ,η)时的二重极限。
正像一元函数的极限一样,二重极限也有类似的运算法则:
二重极限的运算法则
如果当(x,y)→(ξ,η)时,f(x,y)→A,g(x,y)→B.
那末(1):f(x,y)±g(x,y)→A±B;
(2):f(x,y).g(x,y)→A.B;
(3):f(x,y)/g(x,y)→A/B;其中B≠0
像一元函数一样,我们可以利用二重极限来给出二元函数连续的定义:
二元函数的连续性
如果当点(x,y)趋向点(x0,y0)时,函数f(x,y)的二重极限等于f(x,y)在点(x0,y0)处的函数值f(x0,y0),那末称函数f(x,y)在点(x0,y0)处连续.如果f(x,y)在区域D的每一点都连续,那末称它在区域D连续。
如果函数z=f(x,y)在(x0,y0)不满足连续的定义,那末我们就称(x0,y0)是f(x,y)的一个间断点。
关于二元函数间断的问题
二元函数间断点的产生与一元函数的情形类似,但是二元函数间断的情况要比一元函数复杂,它除了有间断点,还有间断线。
二元连续函数的和,差,积,商(分母不为零)和复合函数仍是连续函数。
例题:求下面函数的间断线 成立,
那末常数A称为函数f(x,y)当(x,y)→(ξ,η)时的二重极限。
正像一元函数的极限一样,二重极限也有类似的运算法则:
二重极限的运算法则
如果当(x,y)→(ξ,η)时,f(x,y)→A,g(x,y)→B.
那末(1):f(x,y)±g(x,y)→A±B;
(2):f(x,y).g(x,y)→A.B;
(3):f(x,y)/g(x,y)→A/B;其中B≠0
像一元函数一样,我们可以利用二重极限来给出二元函数连续的定义:
二元函数的连续性
如果当点(x,y)趋向点(x0,y0)时,函数f(x,y)的二重极限等于f(x,y)在点(x0,y0)处的函数值f(x0,y0),那末称函数f(x,y)在点(x0,y0)处连续.如果f(x,y)在区域D的每一点都连续,那末称它在区域D连续。
如果函数z=f(x,y)在(x0,y0)不满足连续的定义,那末我们就称(x0,y0)是f(x,y)的一个间断点。
关于二元函数间断的问题
二元函数间断点的产生与一元函数的情形类似,但是二元函数间断的情况要比一元函数复杂,它除了有间断点,还有间断线。
二元连续函数的和,差,积,商(分母不为零)和复合函数仍是连续函数。
例题:求下面函数的间断线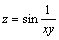 解答:x=0与y=0都是函数
解答:x=0与y=0都是函数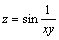 的间断线。 的间断线。 |
|||||||||
|
偏导数 |
|||||||||
在一元函数中,我们已经知道导数就是函数的变化率。对于二元函数我们同样要研究它的"变化率"。然而,由于自变量多了一个,情况就要复杂的多.在xOy平面内,当变点由(x0,y0)沿不同方向变化时,函数f(x,y)的变化快慢一般说来时不同的,因此就需要研究f(x,y)在(x0,y0)点处沿不同方向的变化率。
在这里我们只学习(x,y)沿着平行于x轴和平行于y轴两个特殊方位变动时f(x,y)的变化率。
偏导数的定义
设有二元函数z=f(x,y),点(x0,y0)是其定义域D内一点.把y固定在y0而让x在x0有增量△x,相应地函数
z=f(x,y)有增量(称为对x的偏增量)
△xz=f(x0+△x)-f(x0,y0).
如果△xz与△x之比当△x→0时的极限
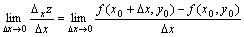 存在,
那末此极限值称为函数z=f(x,y)在(x0,y0)处对x的偏导数。
记作:f'x(x0,y0)或 存在,
那末此极限值称为函数z=f(x,y)在(x0,y0)处对x的偏导数。
记作:f'x(x0,y0)或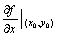 关于对x的偏导数的问题
函数z=f(x,y)在(x0,y0)处对x的偏导数,实际上就是把y固定在y0看成常数后,一元函数z=f(x,y0)在x0处的导数
同样,把x固定在x0,让y有增量△y,如果极限
关于对x的偏导数的问题
函数z=f(x,y)在(x0,y0)处对x的偏导数,实际上就是把y固定在y0看成常数后,一元函数z=f(x,y0)在x0处的导数
同样,把x固定在x0,让y有增量△y,如果极限
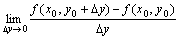 存在,
那末此极限称为函数z=(x,y)在(x0,y0)处对y的偏导数.
记作f'y(x0,y0)或 存在,
那末此极限称为函数z=(x,y)在(x0,y0)处对y的偏导数.
记作f'y(x0,y0)或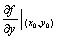 偏导数的求法
当函数z=f(x,y)在(x0,y0)的两个偏导数f'x(x0,y0)与f'y(x0,y0)都存在时,
我们称f(x,y)在(x0,y0)处可导。如果函数f(x,y)在域D的每一点均可导,
那末称函数f(x,y)在域D可导。
此时,对应于域D的每一点(x,y),必有一个对x(对y)的偏导数,因而在域D确定了一个新的二元函数,
称为f(x,y)对x(对y)的偏导函数。简称偏导数。
例题:求z=x2siny的偏导数
解答:把y看作常量对x求导数,得
偏导数的求法
当函数z=f(x,y)在(x0,y0)的两个偏导数f'x(x0,y0)与f'y(x0,y0)都存在时,
我们称f(x,y)在(x0,y0)处可导。如果函数f(x,y)在域D的每一点均可导,
那末称函数f(x,y)在域D可导。
此时,对应于域D的每一点(x,y),必有一个对x(对y)的偏导数,因而在域D确定了一个新的二元函数,
称为f(x,y)对x(对y)的偏导函数。简称偏导数。
例题:求z=x2siny的偏导数
解答:把y看作常量对x求导数,得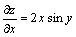 把x看作常量对y求导数,得
把x看作常量对y求导数,得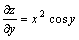 注意:二元函数偏导数的定义和求法可以推广到三元和三元以上函数。
例题:求
注意:二元函数偏导数的定义和求法可以推广到三元和三元以上函数。
例题:求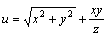 的偏导数。
解答:我们根据二元函数的偏导数的求法来做。
把y和z看成常量对x求导,得 的偏导数。
解答:我们根据二元函数的偏导数的求法来做。
把y和z看成常量对x求导,得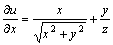 .
把x和z看成常量对y求导,得 .
把x和z看成常量对y求导,得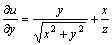 .
把x和y看成常量对z求导,得 .
把x和y看成常量对z求导,得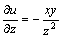 .
高阶偏导数
如果二元函数z=f(x,y)的偏导数f'x(x,y)与f'y(x,y)仍然可导,
那末这两个偏导函数的偏导数称为z=f(x,y)的二阶偏导数。
二元函数的二阶偏导数有四个:f"xx,f"xy,f"yx,f"yy.
注意:f"xy与f"yx的区别在于:前者是先对x求偏导,然后将所得的偏导函数再对y求偏导;后者是先对y求偏导再对x求偏导.当f"xy与f"yx都连续时,求导的结果于求导的先后次序无关。
例题:求函数 .
高阶偏导数
如果二元函数z=f(x,y)的偏导数f'x(x,y)与f'y(x,y)仍然可导,
那末这两个偏导函数的偏导数称为z=f(x,y)的二阶偏导数。
二元函数的二阶偏导数有四个:f"xx,f"xy,f"yx,f"yy.
注意:f"xy与f"yx的区别在于:前者是先对x求偏导,然后将所得的偏导函数再对y求偏导;后者是先对y求偏导再对x求偏导.当f"xy与f"yx都连续时,求导的结果于求导的先后次序无关。
例题:求函数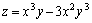 的二阶偏导数.
解答: 的二阶偏导数.
解答: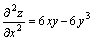 , ,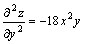 , ,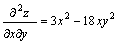 |
|||||||||
|
全微分 |
|||||||||
我们已经学习了一元函数的微分的概念了,现在我们用类似的思想方法来学习多元函数的的全增量,从而把微分的概念推广到多元函数。
这里我们以二元函数为例。
全微分的定义
函数z=f(x,y)的两个偏导数f'x(x,y),f'y(x,y)分别与自变量的增量△x,△y乘积之和
f'x(x,y)△x+f'y(x,y)△y
若该表达式与函数的全增量△z之差,
当ρ→0时,是ρ(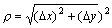 )
的高阶无穷小,
那末该表达式称为函数z=f(x,y)在(x,y)处(关于△x,△y)的全微分。
记作:dz=f'x(x,y)△x+f'y(x,y)△y
注意:其中△z=f'x(x,y)△x+f'y(x,y)△y+αρ,(α是当ρ→0时的无穷小)
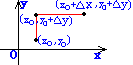
注意:在找函数相应的全增量时,为了使△z与偏导数发生关系,我们把由(x0,y0)变到(x0+△x,y0+△y)的过程分为两部:先由点(x0,y0)变到点(x0,y0+△y),再变到点(x0+△x,y0+△y).其过程如下图所示: )
的高阶无穷小,
那末该表达式称为函数z=f(x,y)在(x,y)处(关于△x,△y)的全微分。
记作:dz=f'x(x,y)△x+f'y(x,y)△y
注意:其中△z=f'x(x,y)△x+f'y(x,y)△y+αρ,(α是当ρ→0时的无穷小)
注意:在找函数相应的全增量时,为了使△z与偏导数发生关系,我们把由(x0,y0)变到(x0+△x,y0+△y)的过程分为两部:先由点(x0,y0)变到点(x0,y0+△y),再变到点(x0+△x,y0+△y).其过程如下图所示:
 例题:求
例题:求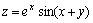 的全微分
解答:由于 的全微分
解答:由于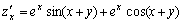 , ,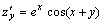 所以
所以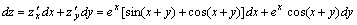 关于全微分的问题
如果偏导数f'x(x,y),f'y(x,y)连续,那末z=f(x,y)一定可微。
关于全微分的问题
如果偏导数f'x(x,y),f'y(x,y)连续,那末z=f(x,y)一定可微。 |
|||||||||
|
多元复合函数的求导法 |
|||||||||
在一元函数中,我们已经知道,复合函数的求导公式在求导法中所起的重要作用,对于多元函数来说也是如此。下面我们来学习多元函数的复合函数的求导公式。我们先以二元函数为例:
多元复合函数的求导公式
链导公式:
设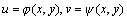 均在(x,y)处可导,函数z=F(u,v)在对应的(u,v)处有连续的一阶偏导数,
那末,复合函数 均在(x,y)处可导,函数z=F(u,v)在对应的(u,v)处有连续的一阶偏导数,
那末,复合函数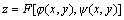 在(x,y)处可导,且有链导公式: 在(x,y)处可导,且有链导公式:
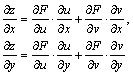 例题:求函数
例题:求函数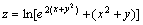 的一阶偏导数
解答:令 的一阶偏导数
解答:令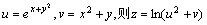 由于
由于
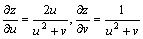 而
而
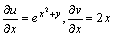 由链导公式可得:
由链导公式可得:
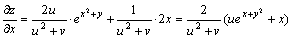
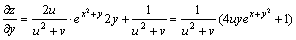 其中
其中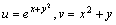 上述公式可以推广到多元,在此不详述。
一个多元复合函数,其一阶偏导数的个数取决于此复合函数自变量的个数。在一阶偏导数的链导公式中,项数的多少取决于与此自变量有关的中间变量的个数。
全导数
由二元函数z=f(u,v)和两个一元函数
上述公式可以推广到多元,在此不详述。
一个多元复合函数,其一阶偏导数的个数取决于此复合函数自变量的个数。在一阶偏导数的链导公式中,项数的多少取决于与此自变量有关的中间变量的个数。
全导数
由二元函数z=f(u,v)和两个一元函数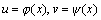 复合起来的函数 复合起来的函数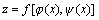 是x的一元函数.
这时复合函数的导数就是一个一元函数的导数 是x的一元函数.
这时复合函数的导数就是一个一元函数的导数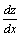 ,称为全导数.
此时的链导公式为: ,称为全导数.
此时的链导公式为:
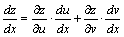 例题:设z=u2v,u=cosx,v=sinx,求
例题:设z=u2v,u=cosx,v=sinx,求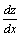 解答:由全导数的链导公式得:
解答:由全导数的链导公式得:
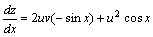 将u=cosx,v=sinx代入上式,得:
将u=cosx,v=sinx代入上式,得:
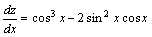 关于全导数的问题
全导数实际上是一元函数的导数,只是求导的过程是借助于偏导数来完成而已。
关于全导数的问题
全导数实际上是一元函数的导数,只是求导的过程是借助于偏导数来完成而已。 |
|||||||||
|
多元函数的极值 |
|||||||||
在一元函数中我们看到,利用函数的导数可以求得函数的极值,从而可以解决一些最大、最小值的应用问题。多元函数也有类似的问题,这里我们只学习二元函数的极值问题。
二元函数极值的定义
如果在(x0,y0)的某一去心邻域内的一切点(x,y)恒有等式:
f(x,y)≤f(x0,y0)
成立,那末就称函数f(x,y)在点(x0,y0)处取得极大值f(x0,y0);如果恒有等式:
f(x,y)≥f(x0,y0)
成立,那末就称函数f(x,y)在点(x0,y0)处取得极小值f(x0,y0).
极大值与极小值统称极值.使函数取得极值的点(x0,y0)称为极值点.
二元可导函数在(x0,y0)取得极值的条件是: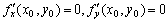 .
注意:此条件只是取得极值的必要条件。
凡是使 .
注意:此条件只是取得极值的必要条件。
凡是使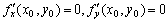 的点(x,y)称为函数f(x,y)的驻点.可导函数的极值点必为驻点,但驻点却不一定是极值点。
二元函数极值判定的方法
设z=f(x,y)在(x0,y0)的某一邻域内有连续的二阶偏导数.如果 的点(x,y)称为函数f(x,y)的驻点.可导函数的极值点必为驻点,但驻点却不一定是极值点。
二元函数极值判定的方法
设z=f(x,y)在(x0,y0)的某一邻域内有连续的二阶偏导数.如果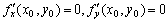 ,那末函数f(x,y)在(x0,y0)取得极值的条件如下表所示: ,那末函数f(x,y)在(x0,y0)取得极值的条件如下表所示:
|
|||||||||
其中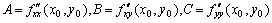 例题:求
例题:求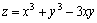 的极值。
解答:设 的极值。
解答:设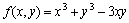 ,则 ,则
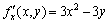 , ,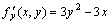 . .
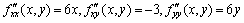 .
解方程组 .
解方程组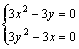 ,得驻点(1,1),(0,0).
对于驻点(1,1)有 ,得驻点(1,1),(0,0).
对于驻点(1,1)有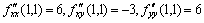 ,故
B2-AC=(-3)2-6.6=-27<0,A=6>0
因此, ,故
B2-AC=(-3)2-6.6=-27<0,A=6>0
因此,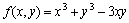 在点(1,1)取得极小值f(1,1)=-1.
对于驻点(0,0)有 在点(1,1)取得极小值f(1,1)=-1.
对于驻点(0,0)有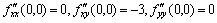 ,故
B2-AC=(-3)2-0.0=9>0
因此, ,故
B2-AC=(-3)2-0.0=9>0
因此,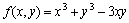 在点(0,0)不取得极值.
多元函数的最大、最小值问题
我们已经知道求一元函数极大值、极小值的步骤,对于多元函数的极大值、极小值的求解也可采用同样的步骤。下面我们给出实际问题中多元函数的极大值、极小值求解步骤。如下:
a):根据实际问题建立函数关系,确定其定义域;
b):求出驻点;
c):结合实际意义判定最大、最小值.
例题:在平面3x+4y-z=26上求一点,使它与坐标原点的距离最短。
解答:a):先建立函数关系,确定定义域
求解与原点的距离最短的问题等价于求解与原点距离的平方 在点(0,0)不取得极值.
多元函数的最大、最小值问题
我们已经知道求一元函数极大值、极小值的步骤,对于多元函数的极大值、极小值的求解也可采用同样的步骤。下面我们给出实际问题中多元函数的极大值、极小值求解步骤。如下:
a):根据实际问题建立函数关系,确定其定义域;
b):求出驻点;
c):结合实际意义判定最大、最小值.
例题:在平面3x+4y-z=26上求一点,使它与坐标原点的距离最短。
解答:a):先建立函数关系,确定定义域
求解与原点的距离最短的问题等价于求解与原点距离的平方
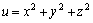 最小的问题.但是P点位于所给的平面上,故z=3x+4y-26.把它代入上式便得到我们所需的函数关系:
最小的问题.但是P点位于所给的平面上,故z=3x+4y-26.把它代入上式便得到我们所需的函数关系:
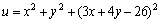 ,-∞<x<+∞,-∞<y<+∞
b):求驻点 ,-∞<x<+∞,-∞<y<+∞
b):求驻点
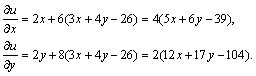 解
解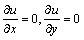 得唯一驻点x=3,y=4.由于点P在所给平面上,故可知
z=-1
c):结合实际意义判定最大、最小值
由问题的实际意义可知,原点与平面距离的最小值是客观存在的,且这个最小值就是极小值.而函数
仅有唯一的驻点.所以,平面上与原点距离最短的点为P(3,4,-1).
从上例我们可以看出,上面函数关系也可看成是:求三元函数 得唯一驻点x=3,y=4.由于点P在所给平面上,故可知
z=-1
c):结合实际意义判定最大、最小值
由问题的实际意义可知,原点与平面距离的最小值是客观存在的,且这个最小值就是极小值.而函数
仅有唯一的驻点.所以,平面上与原点距离最短的点为P(3,4,-1).
从上例我们可以看出,上面函数关系也可看成是:求三元函数
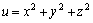 ,
在约束条件
3x+4y-z=26
下的最小值.一个多元函数在一个或几个约束条件下的极值称为条件极值。 ,
在约束条件
3x+4y-z=26
下的最小值.一个多元函数在一个或几个约束条件下的极值称为条件极值。 |
|
空间直角坐标系 |
||||||||||||
空间点的直角坐标系
为了沟通空间图形与数的研究,我们需要建立空间的点与有序数组之间的联系,为此我们通过引进空间直角坐标系来实现。
过定点O,作三条互相垂直的数轴,它们都以O为原点且一般具有相同的长度单位.这三条轴分别叫做x轴(横轴)、y轴(纵轴)、z轴(竖轴);统称坐标轴.通常把x轴和y轴配置在水平面上,而z轴则是铅垂线;它们的正方向要符合右手规则,即以右手握住z轴,当右手的四指从正向x轴以π/2角度转向正向y轴时,大拇指的指向就是z轴的正向,这样的三条坐标轴就组成了一个空间直角坐标系,点O叫做坐标原点。(如下图所示)
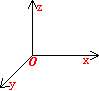 三条坐标轴中的任意两条可以确定一个平面,这样定出的三个平面统称坐标面。
取定了空间直角坐标系后,就可以建立起空间的点与有序数组之间的对应关系。
例:设点M为空间一已知点.我们过点M作三个平面分别垂直于x轴、y轴、z轴,它们与x轴、y轴、z轴的交点依次为P、Q、R,这三点在x轴、y轴、z轴的坐标依次为x、y、z.于是空间的一点M就唯一的确定了一个有序数组x,y,z.这组数x,y,z就叫做点M的坐标,并依次称x,y和z为点M的横坐标,纵坐标和竖坐标。(如下图所示)
三条坐标轴中的任意两条可以确定一个平面,这样定出的三个平面统称坐标面。
取定了空间直角坐标系后,就可以建立起空间的点与有序数组之间的对应关系。
例:设点M为空间一已知点.我们过点M作三个平面分别垂直于x轴、y轴、z轴,它们与x轴、y轴、z轴的交点依次为P、Q、R,这三点在x轴、y轴、z轴的坐标依次为x、y、z.于是空间的一点M就唯一的确定了一个有序数组x,y,z.这组数x,y,z就叫做点M的坐标,并依次称x,y和z为点M的横坐标,纵坐标和竖坐标。(如下图所示)
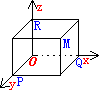 坐标为x,y,z的点M通常记为M(x,y,z).
这样,通过空间直角坐标系,我们就建立了空间的点M和有序数组x,y,z之间的一一对应关系。
注意:坐标面上和坐标轴上的点,其坐标各有一定的特征.
例:如果点M在yOz平面上,则x=0;同样,zOx面上的点,y=0;如果点M在x轴上,则y=z=0;如果M是原点,
则x=y=z=0,等。
空间两点间的距离
设M1(x1,y1,z1)、M2(x2,y2,z2)为空间两点,为了用两点的坐标来表达它们间的距离d我们有公式:
坐标为x,y,z的点M通常记为M(x,y,z).
这样,通过空间直角坐标系,我们就建立了空间的点M和有序数组x,y,z之间的一一对应关系。
注意:坐标面上和坐标轴上的点,其坐标各有一定的特征.
例:如果点M在yOz平面上,则x=0;同样,zOx面上的点,y=0;如果点M在x轴上,则y=z=0;如果M是原点,
则x=y=z=0,等。
空间两点间的距离
设M1(x1,y1,z1)、M2(x2,y2,z2)为空间两点,为了用两点的坐标来表达它们间的距离d我们有公式:
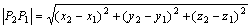 例题:证明以A(4,3,1),B(7,1,2),C(5,2,3)为顶点的三角形△ABC是一等腰三角形.
解答:由两点间距离公式得:
例题:证明以A(4,3,1),B(7,1,2),C(5,2,3)为顶点的三角形△ABC是一等腰三角形.
解答:由两点间距离公式得:
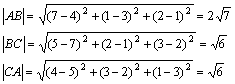 由于
由于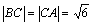 ,所以△ABC是一等腰三角形 ,所以△ABC是一等腰三角形 |
||||||||||||
|
方向余弦与方向数 |
||||||||||||
解析几何中除了两点间的距离外,还有一个最基本的问题就是如何确定有向线段的或有向直线的方向。
方向角与方向余弦
设有空间两点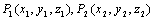 ,若以P1为始点,另一点P2为终点的线段称为有向线段.记作 ,若以P1为始点,另一点P2为终点的线段称为有向线段.记作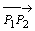 .通过原点作一与其平行且同向的有向线段 .通过原点作一与其平行且同向的有向线段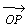 .将 .将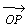 与Ox,Oy,Oz三个坐标轴正向夹角分别记作α,β,γ.这三个角α,β,γ称为有向线段 与Ox,Oy,Oz三个坐标轴正向夹角分别记作α,β,γ.这三个角α,β,γ称为有向线段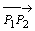 的方向角.其中0≤α≤π,0≤β≤π,0≤γ≤π.
关于方向角的问题
若有向线段的方向确定了,则其方向角也是唯一确定的。
方向角的余弦 的方向角.其中0≤α≤π,0≤β≤π,0≤γ≤π.
关于方向角的问题
若有向线段的方向确定了,则其方向角也是唯一确定的。
方向角的余弦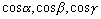 称为有向线段 称为有向线段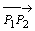 或相应的有向线段的方向余弦。
设有空间两点 或相应的有向线段的方向余弦。
设有空间两点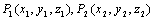 ,则其方向余弦可表示为: ,则其方向余弦可表示为:
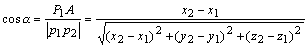
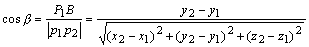
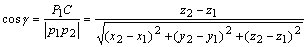 从上面的公式我们可以得到方向余弦之间的一个基本关系式:
从上面的公式我们可以得到方向余弦之间的一个基本关系式:
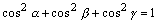 注意:从原点出发的任一单位的有向线段的方向余弦就是其端点坐标。
方向数
方向余弦可以用来确定空间有向直线的方向,但是,如果只需要确定一条空间直线的方位(一条直线的两个方向均确定着同一方位),那末就不一定需要知道方向余弦,而只要知道与方向余弦成比例的三个数就可以了。这三个与方向余弦成比例且不全为零的数A,B,C称为空间直线的方向数,记作:{A,B,C}.即:
注意:从原点出发的任一单位的有向线段的方向余弦就是其端点坐标。
方向数
方向余弦可以用来确定空间有向直线的方向,但是,如果只需要确定一条空间直线的方位(一条直线的两个方向均确定着同一方位),那末就不一定需要知道方向余弦,而只要知道与方向余弦成比例的三个数就可以了。这三个与方向余弦成比例且不全为零的数A,B,C称为空间直线的方向数,记作:{A,B,C}.即:
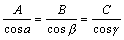 据此我们可得到方向余弦与方向数的转换公式:
据此我们可得到方向余弦与方向数的转换公式:
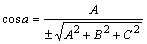 , ,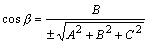 , ,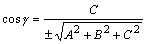 其中:根式取正负号分别得到两组方向余弦,它们代表两个相反的方向。
关于方向数的问题
空间任意两点坐标之差就是联结此两点直线的一组方向数。
两直线的夹角
设L1与L2是空间的任意两条直线,它们可能相交,也可能不相交.通过原点O作平行与两条直线的线段
其中:根式取正负号分别得到两组方向余弦,它们代表两个相反的方向。
关于方向数的问题
空间任意两点坐标之差就是联结此两点直线的一组方向数。
两直线的夹角
设L1与L2是空间的任意两条直线,它们可能相交,也可能不相交.通过原点O作平行与两条直线的线段 .则线段 .则线段 的夹角称为此两直线L1与L2的夹角.
若知道L1与L2的方向余弦则有公式为: 的夹角称为此两直线L1与L2的夹角.
若知道L1与L2的方向余弦则有公式为:
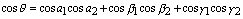 其中:θ为两直线的夹角。
若知道L1与L2的方向数则有公式为:
其中:θ为两直线的夹角。
若知道L1与L2的方向数则有公式为:
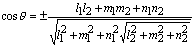 两直线平行、垂直的条件
两直线平行的充分必要条件为:
两直线平行、垂直的条件
两直线平行的充分必要条件为:
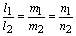 两直线垂直的充分必要条件为:
两直线垂直的充分必要条件为:
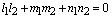 |
||||||||||||
|
平面与空间直线 |
||||||||||||
平面及其方程
我们把与一平面垂直的任一直线称为此平面的法线。
设给定点为Po(x0,y0,z0),给定法线n的一组方向数为{A,B,C}A2+B2+C2≠0,则过此定点且以n为法线的平面方程可表示为:
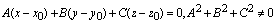 注意:此种形式的方程称为平面方程的点法式。
例题:设直线L的方向数为{3,-4,8},求通过点(2,1,-4)且垂直于直线L的平面方程.
解答:应用上面的公式得所求的平面方程为:
注意:此种形式的方程称为平面方程的点法式。
例题:设直线L的方向数为{3,-4,8},求通过点(2,1,-4)且垂直于直线L的平面方程.
解答:应用上面的公式得所求的平面方程为:
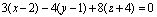 即
即
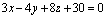 我们把形式为:
Ax+By+Cz+D=0.
称为平面方程的一般式。其中x,y,z的系数A,B,C是平面的法线的一组方向数。
几种特殊位置平面的方程
1、通过原点
其平面方程的一般形式为:
Ax+By+Cz=0.
2、平行于坐标轴
平行于x轴的平面方程的一般形式为:
By+Cz+D=0.
平行于y轴的平面方程的一般形式为:
Ax+Cz+D=0.
平行于z轴的平面方程的一般形式为:
Ax+By+D=0.
3、通过坐标轴
通过x轴的平面方程的一般形式为:
By+Cz=0.
通过y轴和z轴的平面方程的一般形式为:
Ax+Cz=0,Ax+By=0.
4、垂直于坐标轴
垂直于x、y、z轴的平面方程的一般形式为:
Ax+D=0,By+D=0,Cz+D=0.
直线及其方程
任一给定的直线都有着确定的方位.但是,具有某一确定方位的直线可以有无穷多条,它们相互平行.如果要求直线再通过某一定点,则直线便被唯一确定,因而此直线的方程就可由通过它的方向数和定点的坐标表示出来。
设已知直线L的方向数为{l,m,n},又知L上一点Po(x0,y0,z0),则直线L的方程可表示为:
我们把形式为:
Ax+By+Cz+D=0.
称为平面方程的一般式。其中x,y,z的系数A,B,C是平面的法线的一组方向数。
几种特殊位置平面的方程
1、通过原点
其平面方程的一般形式为:
Ax+By+Cz=0.
2、平行于坐标轴
平行于x轴的平面方程的一般形式为:
By+Cz+D=0.
平行于y轴的平面方程的一般形式为:
Ax+Cz+D=0.
平行于z轴的平面方程的一般形式为:
Ax+By+D=0.
3、通过坐标轴
通过x轴的平面方程的一般形式为:
By+Cz=0.
通过y轴和z轴的平面方程的一般形式为:
Ax+Cz=0,Ax+By=0.
4、垂直于坐标轴
垂直于x、y、z轴的平面方程的一般形式为:
Ax+D=0,By+D=0,Cz+D=0.
直线及其方程
任一给定的直线都有着确定的方位.但是,具有某一确定方位的直线可以有无穷多条,它们相互平行.如果要求直线再通过某一定点,则直线便被唯一确定,因而此直线的方程就可由通过它的方向数和定点的坐标表示出来。
设已知直线L的方向数为{l,m,n},又知L上一点Po(x0,y0,z0),则直线L的方程可表示为:
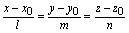 上式就是直线L的方程,这种方程的形式被称为直线方程的对称式。
直线方程也有一般式,它是有两个平面方程联立得到的,如下:
上式就是直线L的方程,这种方程的形式被称为直线方程的对称式。
直线方程也有一般式,它是有两个平面方程联立得到的,如下:
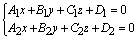 这就是直线方程的一般式。
平面、直线间的平行垂直关系
对于一个给定的平面,它的法线也就可以知道了。因此平面间的平行与垂直关系,也就转化为直线间的平行与垂直关系。平面与直线间的平行与垂直关系,也就是平面的法线与直线的平行与垂直关系。
总的来说,平面、直线间的垂直与平行关系,最终都转化为直线与直线的平行与垂直关系。在此我们就不列举例题了。
这就是直线方程的一般式。
平面、直线间的平行垂直关系
对于一个给定的平面,它的法线也就可以知道了。因此平面间的平行与垂直关系,也就转化为直线间的平行与垂直关系。平面与直线间的平行与垂直关系,也就是平面的法线与直线的平行与垂直关系。
总的来说,平面、直线间的垂直与平行关系,最终都转化为直线与直线的平行与垂直关系。在此我们就不列举例题了。 |
||||||||||||
|
曲面与空间曲线 |
||||||||||||
曲面的方程
我们知道,在平面解析几何中可把曲线看成是动点的轨迹.因此,在空间中曲面可看成是一个动点或一条动曲线(直线)按一定的条件或规律运动而产生的轨迹。
设曲面上动点P的坐标为(x,y,z),由这一条件或规律就能导出一个含有变量x,y,z的方程:
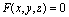 如果此方程当且仅当P为曲面上的点时,才为P点的坐标所满足。那末我们就用这个方程表示曲面,并称这个方程为曲面的方程,把这个曲面称为方程的图形。
空间曲线的方程
我们知道,空间直线可看成两平面的交线,因而它的方程可用此两相交平面的方程的联立方程组来表示,这就是直线方程的一般式。
一般地,空间曲线也可以象空间直线那样看成是两个曲面的交线,因而空间曲线的方程就可由此两相交曲面方程的联立方程组来表示。
设有两个相交曲面,它们的方程是
如果此方程当且仅当P为曲面上的点时,才为P点的坐标所满足。那末我们就用这个方程表示曲面,并称这个方程为曲面的方程,把这个曲面称为方程的图形。
空间曲线的方程
我们知道,空间直线可看成两平面的交线,因而它的方程可用此两相交平面的方程的联立方程组来表示,这就是直线方程的一般式。
一般地,空间曲线也可以象空间直线那样看成是两个曲面的交线,因而空间曲线的方程就可由此两相交曲面方程的联立方程组来表示。
设有两个相交曲面,它们的方程是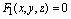 , ,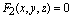 ,那末联立方程组: ,那末联立方程组:
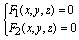 便是它们的交线方程。
两类常见的曲面
1、柱面
设有动直线L沿一给定的曲线C移动,移动时始终与给定的直线M平行,这样由动直线L所形成的曲面称为柱面,动直线L称为柱面的母线,定曲线C称为柱面的准线。
2、旋转面
设有一条平面曲线C,绕着同一平面内的一条直线L旋转一周,这样由C旋转所形成的曲面称为旋转面,曲线C称为旋转面的母线,直线L称为旋转面的轴。
下面我们再列举出几种常见的二次曲面
便是它们的交线方程。
两类常见的曲面
1、柱面
设有动直线L沿一给定的曲线C移动,移动时始终与给定的直线M平行,这样由动直线L所形成的曲面称为柱面,动直线L称为柱面的母线,定曲线C称为柱面的准线。
2、旋转面
设有一条平面曲线C,绕着同一平面内的一条直线L旋转一周,这样由C旋转所形成的曲面称为旋转面,曲线C称为旋转面的母线,直线L称为旋转面的轴。
下面我们再列举出几种常见的二次曲面
|
|
定积分的概念 |
我们先来看一个实际问题---求曲边梯形的面积。
设曲边梯形是有连续曲线y=f(x)、x轴与直线x=a、x=b所围成。如下图所示:
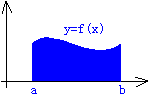 现在计算它的面积A.我们知道矩形面积的求法,但是此图形有一边是一条曲线,该如何求呢?
我们知道曲边梯形在底边上各点处的高f(x)在区间[a,b]上变动,而且它的高是连续变化的,因此在很小的一段区间的变化很小,近似于不变,并且当区间的长度无限缩小时,高的变化也无限减小。因此,如果把区间[a,b]分成许多小区间,在每个小区间上,用其中某一点的高来近似代替同一个小区间上的窄曲变梯形的变高,我们再根据矩形的面积公式,即可求出相应窄曲边梯形面积的近似值,从而求出整个曲边梯形的近似值。
显然:把区间[a,b]分的越细,所求出的面积值越接近于精确值。为此我们产生了定积分的概念。
定积分的概念
设函数f(x)在[a,b]上有界,在[a,b]中任意插入若干个分点
a=x0<x1<...<xn-1<xn=b
把区间[a,b]分成n个小区间
[x0,x1],...[xn-1,xn],
在每个小区间[xi-1,xi]上任取一点ξi(xi-1≤ξi≤xi),作函数值f(ξi)与小区间长度的乘积f(ξi)△xi,
并作出和
现在计算它的面积A.我们知道矩形面积的求法,但是此图形有一边是一条曲线,该如何求呢?
我们知道曲边梯形在底边上各点处的高f(x)在区间[a,b]上变动,而且它的高是连续变化的,因此在很小的一段区间的变化很小,近似于不变,并且当区间的长度无限缩小时,高的变化也无限减小。因此,如果把区间[a,b]分成许多小区间,在每个小区间上,用其中某一点的高来近似代替同一个小区间上的窄曲变梯形的变高,我们再根据矩形的面积公式,即可求出相应窄曲边梯形面积的近似值,从而求出整个曲边梯形的近似值。
显然:把区间[a,b]分的越细,所求出的面积值越接近于精确值。为此我们产生了定积分的概念。
定积分的概念
设函数f(x)在[a,b]上有界,在[a,b]中任意插入若干个分点
a=x0<x1<...<xn-1<xn=b
把区间[a,b]分成n个小区间
[x0,x1],...[xn-1,xn],
在每个小区间[xi-1,xi]上任取一点ξi(xi-1≤ξi≤xi),作函数值f(ξi)与小区间长度的乘积f(ξi)△xi,
并作出和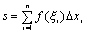 ,
如果不论对[a,b]怎样分法,也不论在小区间上的点ξi怎样取法,只要当区间的长度趋于零时,和S总趋于确定的极限I,
这时我们称这个极限I为函数f(x)在区间[a,b]上的定积分,
记作 ,
如果不论对[a,b]怎样分法,也不论在小区间上的点ξi怎样取法,只要当区间的长度趋于零时,和S总趋于确定的极限I,
这时我们称这个极限I为函数f(x)在区间[a,b]上的定积分,
记作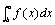 。
即: 。
即: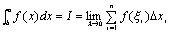 关于定积分的问题
我们有了定积分的概念了,那么函数f(x)满足什么条件时才可积?
定理(1):设f(x)在区间[a,b]上连续,则f(x)在区间[a,b]上可积。
(2):设f(x)在区间[a,b]上有界,且只有有限个间断点,则f(x)在区间[a,b]上可积。
定积分的性质
性质(1):函数的和(差)得定积分等于它们的定积分的和(差).
即:
关于定积分的问题
我们有了定积分的概念了,那么函数f(x)满足什么条件时才可积?
定理(1):设f(x)在区间[a,b]上连续,则f(x)在区间[a,b]上可积。
(2):设f(x)在区间[a,b]上有界,且只有有限个间断点,则f(x)在区间[a,b]上可积。
定积分的性质
性质(1):函数的和(差)得定积分等于它们的定积分的和(差).
即: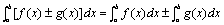 性质(2):被积函数的常数因子可以提到积分号外面.
即:
性质(2):被积函数的常数因子可以提到积分号外面.
即: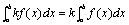 性质(3):如果在区间[a,b]上,f(x)≤g(x),则
性质(3):如果在区间[a,b]上,f(x)≤g(x),则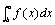 ≤ ≤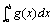 (a<b)
性质(4):设M及m分别是函数f(x)在区间[a,b]上的最大值及最小值,则 m(b-a)≤
(a<b)
性质(4):设M及m分别是函数f(x)在区间[a,b]上的最大值及最小值,则 m(b-a)≤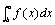 ≤M(b-a)
性质(5):如果f(x)在区间[a,b]上连续,则在积分区间[a,b]上至少存在一点ξ,使下式成立: ≤M(b-a)
性质(5):如果f(x)在区间[a,b]上连续,则在积分区间[a,b]上至少存在一点ξ,使下式成立:
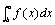 =f(ξ)(b-a)
注:此性质就是定积分中值定理。 =f(ξ)(b-a)
注:此性质就是定积分中值定理。 |
|
微积分积分公式 |
|
积分上限的函数及其导数 设函数f(x)在区间[a,b]上连续,并且设x为[a,b]上的一点.现在我们来考察f(x)在部分区间[a,x]上的定积分 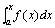 ,我们知道f(x)在[a,x]上仍旧连续,因此此定积分存在。
如果上限x在区间[a,b]上任意变动,则对于每一个取定的x值,定积分有一个对应值,所以它在[a,b]上定义了一个函数,记作φ(x): ,我们知道f(x)在[a,x]上仍旧连续,因此此定积分存在。
如果上限x在区间[a,b]上任意变动,则对于每一个取定的x值,定积分有一个对应值,所以它在[a,b]上定义了一个函数,记作φ(x): 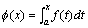 注意:为了明确起见,我们改换了积分变量(定积分与积分变量的记法无关)
定理(1):如果函数f(x)在区间[a,b]上连续,则积分上限的函数
注意:为了明确起见,我们改换了积分变量(定积分与积分变量的记法无关)
定理(1):如果函数f(x)在区间[a,b]上连续,则积分上限的函数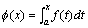 在[a,b]上具有导数,
并且它的导数是 在[a,b]上具有导数,
并且它的导数是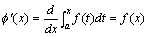 (a≤x≤b)
(2):如果函数f(x)在区间[a,b]上连续,则函数
(a≤x≤b)
(2):如果函数f(x)在区间[a,b]上连续,则函数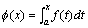 就是f(x)在[a,b]上的一个原函数。
注意:定理(2)即肯定了连续函数的原函数是存在的,又初步揭示了积分学中的定积分与原函数之间的联系。 就是f(x)在[a,b]上的一个原函数。
注意:定理(2)即肯定了连续函数的原函数是存在的,又初步揭示了积分学中的定积分与原函数之间的联系。牛顿--莱布尼兹公式 定理(3):如果函数F(x)是连续函数f(x)在区间[a,b]上的一个原函数,则 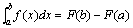 注意:此公式被称为牛顿-莱布尼兹公式,它进一步揭示了定积分与原函数(不定积分)之间的联系。
它表明:一个连续函数在区间[a,b]上的定积分等于它的任一个原函数再去见[a,b]上的增量。因此它就
给定积分提供了一个有效而简便的计算方法。
例题:求
注意:此公式被称为牛顿-莱布尼兹公式,它进一步揭示了定积分与原函数(不定积分)之间的联系。
它表明:一个连续函数在区间[a,b]上的定积分等于它的任一个原函数再去见[a,b]上的增量。因此它就
给定积分提供了一个有效而简便的计算方法。
例题:求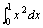 解答:我们由牛顿-莱布尼兹公式得:
解答:我们由牛顿-莱布尼兹公式得: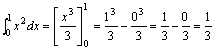 注意:通常也把牛顿--莱布尼兹公式称作微积分基本公式。
注意:通常也把牛顿--莱布尼兹公式称作微积分基本公式。 |
|
定积分的换元法与分部积分法 |
定积分的换元法
我们知道求定积分可以转化为求原函数的增量,在前面我们又知道用换元法可以求出一些函数的原函数。因此,在一定条件下,可以用换元法来计算定积分。
定理:设函数f(x)在区间[a,b]上连续;函数g(t)在区间[m,n]上是单值的且有连续导数;当t在区间[m,n]上变化时,x=g(t)的值在[a,b]上变化,且g(m)=a,g(n)=b;则有定积分的换元公式:
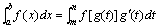 例题:计算
例题:计算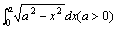 解答:设x=asint,则dx=acostdt,且当x=0时,t=0;当x=a时,t=π/2.于是:
解答:设x=asint,则dx=acostdt,且当x=0时,t=0;当x=a时,t=π/2.于是:
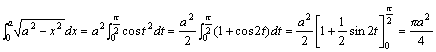 注意:在使用定积分的换元法时,当积分变量变换时,积分的上下限也要作相应的变换。
定积分的分部积分法
计算不定积分有分部积分法,相应地,计算定积分也有分部积分法。
设u(x)、v(x)在区间[a,b]上具有连续导数u'(x)、v'(x),则有(uv)'=u'v+uv',分别求此等式两端在[a,b]上的定积分,并移向得:
注意:在使用定积分的换元法时,当积分变量变换时,积分的上下限也要作相应的变换。
定积分的分部积分法
计算不定积分有分部积分法,相应地,计算定积分也有分部积分法。
设u(x)、v(x)在区间[a,b]上具有连续导数u'(x)、v'(x),则有(uv)'=u'v+uv',分别求此等式两端在[a,b]上的定积分,并移向得: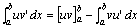 上式即为定积分的分部积分公式。
例题:计算
上式即为定积分的分部积分公式。
例题:计算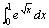 解答:设
解答:设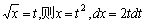 ,且当x=0时,t=0;当x=1时,t=1.由前面的换元公式得: ,且当x=0时,t=0;当x=1时,t=1.由前面的换元公式得: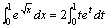 再用分部积分公式计算上式的右端的积分。设u=t,dv=etdt,则du=dt,v=et.于是:
再用分部积分公式计算上式的右端的积分。设u=t,dv=etdt,则du=dt,v=et.于是:
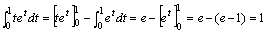 故:
故: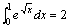 |
|
广义积分 |
在一些实际问题中,我们常遇到积分区间为无穷区间,或者被积函数在积分区间上具有无穷间断点的积分,它们已不属于前面我们所学习的定积分了。为此我们对定积分加以推广,也就是---广义积分。
一:积分区间为无穷区间的广义积分
设函数f(x)在区间[a,+∞)上连续,取b>a.如果极限
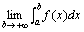 存在,
则此极限叫做函数f(x)在无穷区间[a,+∞)上的广义积分,
记作: 存在,
则此极限叫做函数f(x)在无穷区间[a,+∞)上的广义积分,
记作: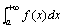 ,
即: ,
即: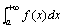 = =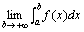 .
此时也就是说广义积分 .
此时也就是说广义积分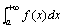 收敛。如果上述即先不存在,则说广义积分 收敛。如果上述即先不存在,则说广义积分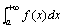 发散,此时虽然用同样的记号,但它已不表示数值了。
类似地,设函数f(x)在区间(-∞,b]上连续,取a<b.如果极限 发散,此时虽然用同样的记号,但它已不表示数值了。
类似地,设函数f(x)在区间(-∞,b]上连续,取a<b.如果极限
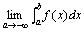 存在,
则此极限叫做函数f(x)在无穷区间(-∞,b]上的广义积分,
记作: 存在,
则此极限叫做函数f(x)在无穷区间(-∞,b]上的广义积分,
记作: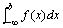 ,
即: ,
即: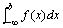 = =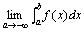 .
此时也就是说广义积分 .
此时也就是说广义积分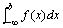 收敛。如果上述极限不存在,就说广义积分 收敛。如果上述极限不存在,就说广义积分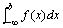 发散。
如果广义积分 发散。
如果广义积分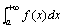 和 和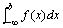 都收敛,则称上述两广义积分之和为函数f(x)在无穷区间(-∞,+∞)上的广义积分,
记作: 都收敛,则称上述两广义积分之和为函数f(x)在无穷区间(-∞,+∞)上的广义积分,
记作: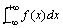 ,
即: ,
即: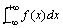 = =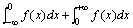 上述广义积分统称积分区间为无穷的广义积分。
例题:计算广义积分
上述广义积分统称积分区间为无穷的广义积分。
例题:计算广义积分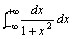 解答:
解答: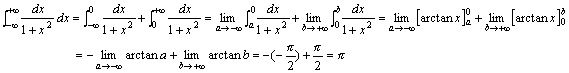 |
二:积分区间有无穷间断点的广义积分
设函数f(x)在(a,b]上连续,而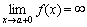 .取ε>0,如果极限 .取ε>0,如果极限
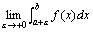 存在,则极限叫做函数f(x)在(a,b]上的广义积分,
仍然记作: 存在,则极限叫做函数f(x)在(a,b]上的广义积分,
仍然记作: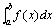 .
即: .
即: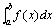 = =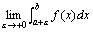 ,
这时也说广义积分 ,
这时也说广义积分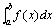 收敛.如果上述极限不存在,就说广义积分 收敛.如果上述极限不存在,就说广义积分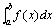 发散。
类似地,设f(x)在[a,b)上连续,而 发散。
类似地,设f(x)在[a,b)上连续,而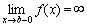 .取ε>0,如果极限 .取ε>0,如果极限
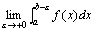 存在,
则定义 存在,
则定义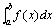 = =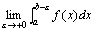 ;
否则就说广义积分 ;
否则就说广义积分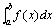 发散。
又,设f(x)在[a,b]上除点c(a<c<b)外连续,而 发散。
又,设f(x)在[a,b]上除点c(a<c<b)外连续,而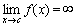 .如果两个广义积分 .如果两个广义积分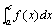 和 和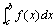 都收敛,
则定义: 都收敛,
则定义: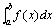 = =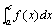 + +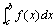 .
否则就说广义积分 .
否则就说广义积分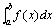 发散。
例题:计算广义积分 发散。
例题:计算广义积分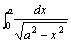 (a>0)
解答:因为 (a>0)
解答:因为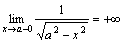 ,所以x=a为被积函数的无穷间断点,于是我们有上面所学得公式可得: ,所以x=a为被积函数的无穷间断点,于是我们有上面所学得公式可得:
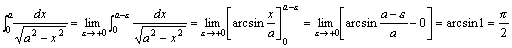 |
|
不定积分的概念 |
原函数的概念
已知函数f(x)是一个定义在某区间的函数,如果存在函数F(x),使得在该区间内的任一点都有
dF'(x)=f(x)dx,
则在该区间内就称函数F(x)为函数f(x)的原函数。
例:sinx是cosx的原函数。
关于原函数的问题
函数f(x)满足什么条件是,才保证其原函数一定存在呢?这个问题我们以后来解决。若其存在原函数,那末原函数一共有多少个呢?
我们可以明显的看出来:若函数F(x)为函数f(x)的原函数,
即:F"(x)=f(x),
则函数族F(x)+C(C为任一个常数)中的任一个函数一定是f(x)的原函数,
故:若函数f(x)有原函数,那末其原函数为无穷多个.
不定积分的概念
函数f(x)的全体原函数叫做函数f(x)的不定积分,
记作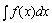 。
由上面的定义我们可以知道:如果函数F(x)为函数f(x)的一个原函数,那末f(x)的不定积分 。
由上面的定义我们可以知道:如果函数F(x)为函数f(x)的一个原函数,那末f(x)的不定积分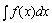 就是函数族
F(x)+C.
即: 就是函数族
F(x)+C.
即: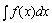 =F(x)+C
例题:求: =F(x)+C
例题:求: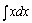 .
解答:由于 .
解答:由于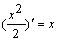 ,故 ,故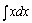 = =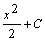 不定积分的性质
1、函数的和的不定积分等于各个函数的不定积分的和;
即:
不定积分的性质
1、函数的和的不定积分等于各个函数的不定积分的和;
即: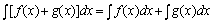 2、求不定积分时,被积函数中不为零的常数因子可以提到积分号外面来,
即:
2、求不定积分时,被积函数中不为零的常数因子可以提到积分号外面来,
即: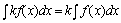 |
|
求不定积分的方法 |
换元法
换元法(一):设f(u)具有原函数F(u),u=g(x)可导,那末F[g(x)]是f[g(x)]g'(x)的原函数.
即有换元公式: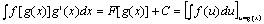 例题:求
例题:求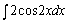 解答:这个积分在基本积分表中是查不到的,故我们要利用换元法。
设u=2x,那末cos2x=cosu,du=2dx,因此:
解答:这个积分在基本积分表中是查不到的,故我们要利用换元法。
设u=2x,那末cos2x=cosu,du=2dx,因此:
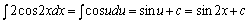 换元法(二):设x=g(t)是单调的,可导的函数,并且g'(t)≠0,又设f[g(t)]g'(t)具有原函数φ(t),
则φ[g(x)]是f(x)的原函数.(其中g(x)是x=g(t)的反函数)
即有换元公式:
换元法(二):设x=g(t)是单调的,可导的函数,并且g'(t)≠0,又设f[g(t)]g'(t)具有原函数φ(t),
则φ[g(x)]是f(x)的原函数.(其中g(x)是x=g(t)的反函数)
即有换元公式: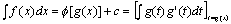 例题:求
例题:求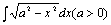 解答:这个积分的困难在于有根式,但是我们可以利用三角公式来换元.
设x=asint(-π/2<t<π/2),那末
解答:这个积分的困难在于有根式,但是我们可以利用三角公式来换元.
设x=asint(-π/2<t<π/2),那末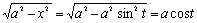 ,dx=acostdt,于是有: ,dx=acostdt,于是有:
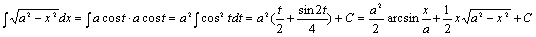 关于换元法的问题
不定积分的换元法是在复合函数求导法则的基础上得来的,我们应根据具体实例来选择所用的方法,求不定积分不象求导那样有规则可依,因此要想熟练的求出某函数的不定积分,只有作大量的练习。
分部积分法
这种方法是利用两个函数乘积的求导法则得来的。
设函数u=u(x)及v=v(x)具有连续导数.我们知道,两个函数乘积的求导公式为:
(uv)'=u'v+uv',移项,得
uv'=(uv)'-u'v,对其两边求不定积分得:
关于换元法的问题
不定积分的换元法是在复合函数求导法则的基础上得来的,我们应根据具体实例来选择所用的方法,求不定积分不象求导那样有规则可依,因此要想熟练的求出某函数的不定积分,只有作大量的练习。
分部积分法
这种方法是利用两个函数乘积的求导法则得来的。
设函数u=u(x)及v=v(x)具有连续导数.我们知道,两个函数乘积的求导公式为:
(uv)'=u'v+uv',移项,得
uv'=(uv)'-u'v,对其两边求不定积分得:
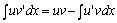 ,
这就是分部积分公式
例题:求 ,
这就是分部积分公式
例题:求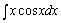 解答:这个积分用换元法不易得出结果,我们来利用分部积分法。
设u=x,dv=cosxdx,那末du=dx,v=sinx,代入分部积分公式得:
解答:这个积分用换元法不易得出结果,我们来利用分部积分法。
设u=x,dv=cosxdx,那末du=dx,v=sinx,代入分部积分公式得:
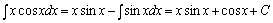 关于分部积分法的问题
在使用分部积分法时,应恰当的选取u和dv,否则就会南辕北辙。选取u和dv一般要考虑两点:
(1)v要容易求得;
(2)
关于分部积分法的问题
在使用分部积分法时,应恰当的选取u和dv,否则就会南辕北辙。选取u和dv一般要考虑两点:
(1)v要容易求得;
(2) 容易积出。 容易积出。 |
|
几种特殊类型函数的积分举例 |
有理函数的积分举例
有理函数是指两个多项式的商所表示的函数,当分子的最高项的次数大于分母最高项的次数时称之为假分式,
反之为真分式。
在求有理函数的不定积分时,若有理函数为假分式应先利用多项式的除法,把一个假分式化成一个多项式和一个真分式之和的形式,然后再求之。
例题:求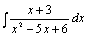 解答:
解答:
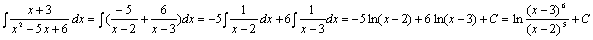 关于有理函数积分的问题
有理函数积分的具体方法请大家参照有关书籍,请谅。
三角函数的有理式的积分举例
三角函数的有理式是指由三角函数和常数经过有限次四则运算所构成的函数。
例题:求
关于有理函数积分的问题
有理函数积分的具体方法请大家参照有关书籍,请谅。
三角函数的有理式的积分举例
三角函数的有理式是指由三角函数和常数经过有限次四则运算所构成的函数。
例题:求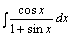 解答:
解答: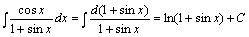 关于三角函数的有理式的积分的问题
任何三角函数都可用正弦与余弦函数表出,故变量代换u=tan(x/2)对三角函数的有理式的积分应用,在此我
们不再举例。
简单无理函数的积分举例
例题:求
关于三角函数的有理式的积分的问题
任何三角函数都可用正弦与余弦函数表出,故变量代换u=tan(x/2)对三角函数的有理式的积分应用,在此我
们不再举例。
简单无理函数的积分举例
例题:求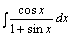 解答:设
解答:设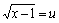 ,于是x=u2+1,dx=2udu,从而所求积分为: ,于是x=u2+1,dx=2udu,从而所求积分为:
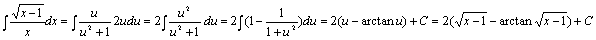 |
|
微分学中值定理 |
|
在给出微分学中值定理的数学定义之前,我们先从几何的角度看一个问题,如下: |
设有连续函数 ,a与b是它定义区间内的两点(a<b),假定此函数在(a,b)处处可导,也就是在(a,b)内的函数图形上处处都由切线,那末我们从图形上容易直到, ,a与b是它定义区间内的两点(a<b),假定此函数在(a,b)处处可导,也就是在(a,b)内的函数图形上处处都由切线,那末我们从图形上容易直到,
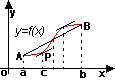 差商
差商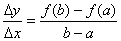 就是割线AB的斜率,若我们把割线AB作平行于自身的移动,那么至少有一次机会达到离割线最远的一点P(x=c)处成为曲线的切线,而曲线的斜率为 就是割线AB的斜率,若我们把割线AB作平行于自身的移动,那么至少有一次机会达到离割线最远的一点P(x=c)处成为曲线的切线,而曲线的斜率为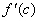 ,由于切线与割线是平行的,因此 ,由于切线与割线是平行的,因此
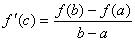 成立。
注:这个结果就称为微分学中值定理,也称为拉格朗日中值定理 成立。
注:这个结果就称为微分学中值定理,也称为拉格朗日中值定理 |
拉格朗日中值定理
如果函数 在闭区间[a,b]上连续,在开区间(a,b)内可导,那末在(a,b)内至少有一点c,使 在闭区间[a,b]上连续,在开区间(a,b)内可导,那末在(a,b)内至少有一点c,使
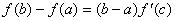 成立。 成立。 |
这个定理的特殊情形,即: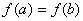 的情形,称为罗尔定理。描述如下:
若 的情形,称为罗尔定理。描述如下:
若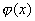 在闭区间[a,b]上连续,在开区间(a,b)内可导,且 在闭区间[a,b]上连续,在开区间(a,b)内可导,且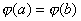 ,那末在(a,b)内至少有一点c,使 ,那末在(a,b)内至少有一点c,使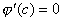 成立。
注:这个定理是罗尔在17世纪初,在微积分发明之前以几何的形式提出来的。
注:在此我们对这两个定理不加以证明,若有什么疑问,请参考相关书籍 成立。
注:这个定理是罗尔在17世纪初,在微积分发明之前以几何的形式提出来的。
注:在此我们对这两个定理不加以证明,若有什么疑问,请参考相关书籍 |
下面我们在学习一条通过拉格朗日中值定理推广得来的定理--柯西中值定理
柯西中值定理
如果函数 , ,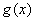 在闭区间[a,b]上连续,在开区间(a,b)内可导,且 在闭区间[a,b]上连续,在开区间(a,b)内可导,且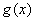 ≠0,那末在(a,b)内至少有一点c,使 ≠0,那末在(a,b)内至少有一点c,使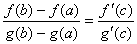 成立。 成立。 |
例题:证明方程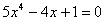 在0与1之间至少有一个实根
证明:不难发现方程左端 在0与1之间至少有一个实根
证明:不难发现方程左端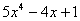 是函数 是函数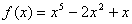 的导数: 的导数: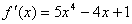 函数
函数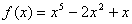 在[0,1]上连续,在(0,1)内可导,且 在[0,1]上连续,在(0,1)内可导,且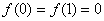 ,由罗尔定理
可知,在0与1之间至少有一点c,使 ,由罗尔定理
可知,在0与1之间至少有一点c,使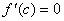 ,即 ,即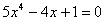 也就是:方程
也就是:方程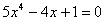 在0与1之间至少有一个实根 在0与1之间至少有一个实根 |
|
未定式问题 |
问题:什么样的式子称作未定式呢?
答案:对于函数 , ,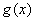 来说,当x→a(或x→∞)时,函数 来说,当x→a(或x→∞)时,函数 , ,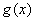 都趋于零或无穷大
则极限 都趋于零或无穷大
则极限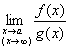 可能存在,也可能不存在,我们就把式子 可能存在,也可能不存在,我们就把式子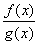 称为未定式。分别记为 称为未定式。分别记为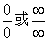 型 型 |
|
我们容易知道,对于未定式的极限求法,是不能应用"商的极限等于极限的商"这个法则来求解的,那么我们该如何求这类问题的极限呢?
下面我们来学习罗彼塔(L'Hospital)法则,它就是这个问题的答案
注:它是根据柯西中值定理推出来的。 |
罗彼塔(L'Hospital)法则
当x→a(或x→∞)时,函数 , ,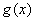 都趋于零或无穷大,在点a的某个去心邻域内(或当│x│>N)时, 都趋于零或无穷大,在点a的某个去心邻域内(或当│x│>N)时,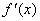 与 与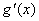 都存在, 都存在,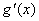 ≠0,且 ≠0,且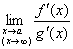 存在
则: 存在
则: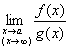 = =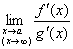 这种通过分子分母求导再来求极限来确定未定式的方法,就是所谓的罗彼塔(L'Hospital)法则
注:它是以前求极限的法则的补充,以前利用法则不好求的极限,可利用此法则求解。
这种通过分子分母求导再来求极限来确定未定式的方法,就是所谓的罗彼塔(L'Hospital)法则
注:它是以前求极限的法则的补充,以前利用法则不好求的极限,可利用此法则求解。 |
例题:求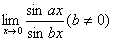 解答:容易看出此题利用以前所学的法则是不易求解的,因为它是未定式中的
解答:容易看出此题利用以前所学的法则是不易求解的,因为它是未定式中的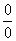 型求解问题,因此我们就可以利用上面所学的法则了。 型求解问题,因此我们就可以利用上面所学的法则了。
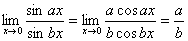 |
例题:求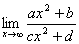 解答:此题为未定式中的
解答:此题为未定式中的 型求解问题,利用罗彼塔法则来求解 型求解问题,利用罗彼塔法则来求解
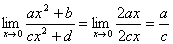 |
另外,若遇到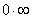 、 、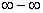 、 、
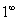 、 、
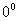 、 、
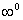 等型,通常是转化为 等型,通常是转化为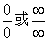 型后,在利用法则求解。 型后,在利用法则求解。 |
例题:求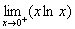 解答:此题利用以前所学的法则是不好求解的,它为
解答:此题利用以前所学的法则是不好求解的,它为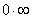 型,故可先将其转化为 型,故可先将其转化为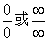 型后在求解, 型后在求解,
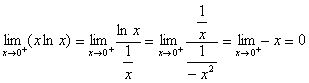 |
注:罗彼塔法则只是说明:对未定式来说,当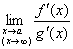 存在,则 存在,则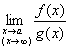 存在且二者的极限相同;而并不是 存在且二者的极限相同;而并不是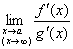 不存在时, 不存在时,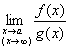 也不存在,此时只是说明了罗彼塔法则存在的条件破列。 也不存在,此时只是说明了罗彼塔法则存在的条件破列。 |
|
函数单调性的判定法 |
|
函数的单调性也就是函数的增减性,怎样才能判断函数的增减性呢?
我们知道若函数在某区间上单调增(或减),则在此区间内函数图形上切线的斜率均为正(或负),也就是函数的导数在此区间上均取正值(或负值).因此我们可通过判定函数导数的正负来判定函数的增减性. |
判定方法:
设函数 在[a,b]上连续,在(a,b)内可导.
a):如果在(a,b)内 在[a,b]上连续,在(a,b)内可导.
a):如果在(a,b)内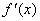 >0,那末函数 >0,那末函数 在[a,b]上单调增加;
b):如果在(a,b)内 在[a,b]上单调增加;
b):如果在(a,b)内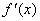 <0,那末函数 <0,那末函数 在[a,b]上单调减少. 在[a,b]上单调减少. |
例题:确定函数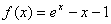 的增减区间.
解答:容易确定此函数的定义域为(-∞,+∞)
其导数为: 的增减区间.
解答:容易确定此函数的定义域为(-∞,+∞)
其导数为: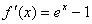 ,因此可以判出:
当x>0时, ,因此可以判出:
当x>0时,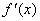 >0,故它的单调增区间为(0,+∞);
当x<0时, >0,故它的单调增区间为(0,+∞);
当x<0时,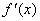 <0,故它的单调减区间为(-∞,0);
注:此判定方法若反过来讲,则是不正确的。 <0,故它的单调减区间为(-∞,0);
注:此判定方法若反过来讲,则是不正确的。 |
|
函数的极值及其求法
|
在学习函数的极值之前,我们先来看一例子:
设有函数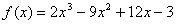 ,容易知道点x=1及x=2是此函数单调区间的分界点,又可知在点x=1左侧附近,函数值是单调增加的,在点x=1右侧附近,函数值是单调减小的.因此存在着点x=1的一个邻域,对于这个邻域内,任何点x(x=1除外), ,容易知道点x=1及x=2是此函数单调区间的分界点,又可知在点x=1左侧附近,函数值是单调增加的,在点x=1右侧附近,函数值是单调减小的.因此存在着点x=1的一个邻域,对于这个邻域内,任何点x(x=1除外), < <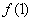 均成立,点x=2也有类似的情况(在此不多说),为什么这些点有这些性质呢?
事实上,这就是我们将要学习的内容--函数的极值, 均成立,点x=2也有类似的情况(在此不多说),为什么这些点有这些性质呢?
事实上,这就是我们将要学习的内容--函数的极值, |
函数极值的定义
设函数 在区间(a,b)内有定义,x0是(a,b)内一点.
若存在着x0点的一个邻域,对于这个邻域内任何点x(x0点除外), 在区间(a,b)内有定义,x0是(a,b)内一点.
若存在着x0点的一个邻域,对于这个邻域内任何点x(x0点除外), < <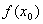 均成立,
则说 均成立,
则说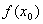 是函数 是函数 的一个极大值;
若存在着x0点的一个邻域,对于这个邻域内任何点x(x0点除外), 的一个极大值;
若存在着x0点的一个邻域,对于这个邻域内任何点x(x0点除外), > >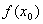 均成立,
则说 均成立,
则说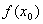 是函数 是函数 的一个极小值.
函数的极大值与极小值统称为函数的极值,使函数取得极值的点称为极值点。
我们知道了函数极值的定义了,怎样求函数的极值呢?
学习这个问题之前,我们再来学习一个概念--驻点
凡是使 的一个极小值.
函数的极大值与极小值统称为函数的极值,使函数取得极值的点称为极值点。
我们知道了函数极值的定义了,怎样求函数的极值呢?
学习这个问题之前,我们再来学习一个概念--驻点
凡是使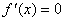 的x点,称为函数 的x点,称为函数 的驻点。
判断极值点存在的方法有两种:如下 的驻点。
判断极值点存在的方法有两种:如下 |
方法一:
设函数 在x0点的邻域可导,且 在x0点的邻域可导,且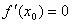 .
情况一:若当x取x0左侧邻近值时, .
情况一:若当x取x0左侧邻近值时,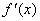 >0,当x取x0右侧邻近值时, >0,当x取x0右侧邻近值时,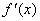 <0,
则函数 <0,
则函数 在x0点取极大值。
情况一:若当x取x0左侧邻近值时, 在x0点取极大值。
情况一:若当x取x0左侧邻近值时,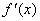 <0,当x取x0右侧邻近值时, <0,当x取x0右侧邻近值时,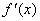 >0,
则函数 >0,
则函数 在x0点取极小值。
注:此判定方法也适用于导数在x0点不存在的情况。
用方法一求极值的一般步骤是:
a):求 在x0点取极小值。
注:此判定方法也适用于导数在x0点不存在的情况。
用方法一求极值的一般步骤是:
a):求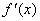 ;
b):求 ;
b):求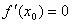 的全部的解--驻点;
c):判断 的全部的解--驻点;
c):判断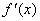 在驻点两侧的变化规律,即可判断出函数的极值。 在驻点两侧的变化规律,即可判断出函数的极值。 |
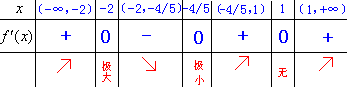
例题:求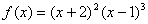 极值点
解答:先求导数 极值点
解答:先求导数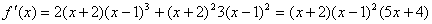 再求出驻点:当
再求出驻点:当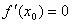 时,x=-2、1、-4/5
判定函数的极值,如下图所示 时,x=-2、1、-4/5
判定函数的极值,如下图所示
 |
方法二:
设函数 在x0点具有二阶导数,且 在x0点具有二阶导数,且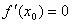 时 时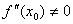 .
则:a):当 .
则:a):当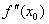 <0,函数 <0,函数 在x0点取极大值;
b):当 在x0点取极大值;
b):当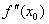 >0,函数 >0,函数 在x0点取极小值;
c):当 在x0点取极小值;
c):当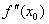 =0,其情形不一定,可由方法一来判定. =0,其情形不一定,可由方法一来判定. |
例题:我们仍以例1为例,以比较这两种方法的区别。
解答:上面我们已求出了此函数的驻点,下面我们再来求它的二阶导数。
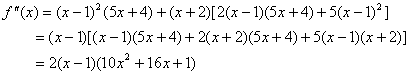
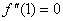 ,故此时的情形不确定,我们可由方法一来判定; ,故此时的情形不确定,我们可由方法一来判定;
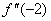 <0,故此点为极大值点; <0,故此点为极大值点;
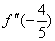 >0,故此点为极小值点。 >0,故此点为极小值点。 |
|
函数的最大值、最小值及其应用 |
在工农业生产、工程技术及科学实验中,常会遇到这样一类问题:在一定条件下,怎样使"产品最多"、"用料最省"、"成本最低"等。
这类问题在数学上可归结为求某一函数的最大值、最小值的问题。
怎样求函数的最大值、最小值呢?前面我们已经知道了,函数的极值是局部的。要求 在[a,b]上的最大值、最小值时,可求出开区间(a,b)内全部的极值点,加上端点 在[a,b]上的最大值、最小值时,可求出开区间(a,b)内全部的极值点,加上端点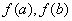 的值,从中取得最大值、最小值即为所求。 的值,从中取得最大值、最小值即为所求。 |
例题:求函数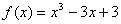 ,在区间[-3,3/2]的最大值、最小值。
解答: ,在区间[-3,3/2]的最大值、最小值。
解答: 在此区间处处可导,
先来求函数的极值 在此区间处处可导,
先来求函数的极值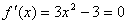 ,故x=±1,
再来比较端点与极值点的函数值,取出最大值与最小值即为所求。
因为 ,故x=±1,
再来比较端点与极值点的函数值,取出最大值与最小值即为所求。
因为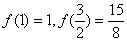 , ,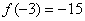 , ,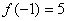 ,
故函数的最大值为 ,
故函数的最大值为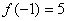 ,函数的最小值为 ,函数的最小值为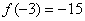 。 。 |
例题:圆柱形罐头,高度H与半径R应怎样配,使同样容积下材料最省?
解答:由题意可知: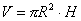 为一常数,
面积 为一常数,
面积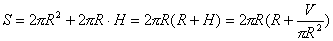 故在V不变的条件下,改变R使S取最小值。
故在V不变的条件下,改变R使S取最小值。
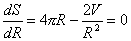
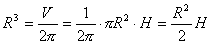 故:
故: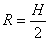 时,用料最省。 时,用料最省。 |
|
曲线的凹向与拐点 |
通过前面的学习,我们知道由一阶导数的正负,可以判定出函数的单调区间与极值,但是还不能进一步研究曲线的性态,为此我们还要了解曲线的凹性。
定义:
对区间I的曲线 作切线,如果曲线弧在所有切线的下面,则称曲线在区间I下凹,如果曲线在切线的上面,称曲线在区间I上凹。 作切线,如果曲线弧在所有切线的下面,则称曲线在区间I下凹,如果曲线在切线的上面,称曲线在区间I上凹。 |
曲线凹向的判定定理
定理一:设函数 在区间(a,b)上可导,它对应曲线是向上凹(或向下凹)的充分必要条件是:
导数 在区间(a,b)上可导,它对应曲线是向上凹(或向下凹)的充分必要条件是:
导数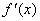 在区间(a,b)上是单调增(或单调减)。
定理二:设函数 在区间(a,b)上是单调增(或单调减)。
定理二:设函数 在区间(a,b)上可导,并且具有一阶导数和二阶导数;那末:
若在(a,b)内, 在区间(a,b)上可导,并且具有一阶导数和二阶导数;那末:
若在(a,b)内,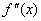 >0,则 >0,则 在[a,b]对应的曲线是下凹的;
若在(a,b)内, 在[a,b]对应的曲线是下凹的;
若在(a,b)内,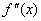 <0,则 <0,则 在[a,b]对应的曲线是上凹的; 在[a,b]对应的曲线是上凹的; |
例题:判断函数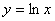 的凹向
解答:我们根据定理二来判定。
因为 的凹向
解答:我们根据定理二来判定。
因为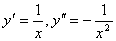 ,所以在函数 ,所以在函数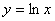 的定义域(0,+∞)内, 的定义域(0,+∞)内,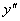 <0,
故函数所对应的曲线时下凹的。 <0,
故函数所对应的曲线时下凹的。 |
|
拐点的定义
连续函数上,上凹弧与下凹弧的分界点称为此曲线上的拐点。 |
拐定的判定方法
如果 在区间(a,b)内具有二阶导数,我们可按下列步骤来判定 在区间(a,b)内具有二阶导数,我们可按下列步骤来判定 的拐点。
(1):求 的拐点。
(1):求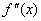 ;
(2):令 ;
(2):令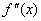 =0,解出此方程在区间(a,b)内实根;
(3):对于(2)中解出的每一个实根x0,检查 =0,解出此方程在区间(a,b)内实根;
(3):对于(2)中解出的每一个实根x0,检查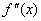 在x0左、右两侧邻近的符号,若符号相反,则此点是拐点,若相同,则不是拐点。 在x0左、右两侧邻近的符号,若符号相反,则此点是拐点,若相同,则不是拐点。 |
例题:求曲线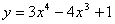 的拐点。
解答:由 的拐点。
解答:由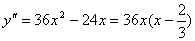 ,
令 ,
令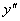 =0,得x=0,2/3
判断 =0,得x=0,2/3
判断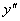 在0,2/3左、右两侧邻近的符号,可知此两点皆是曲线的拐点。 在0,2/3左、右两侧邻近的符号,可知此两点皆是曲线的拐点。 |
导数的概念
在学习到数的概念之前,我们先来讨论一下物理学中变速直线运动的瞬时速度的问题。例:设一质点沿x轴运动时,其位置x是时间t的函数,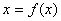 ,求质点在t0的瞬时速度?我们知道时间从t0有增量△t时,质点的位置有增量
,求质点在t0的瞬时速度?我们知道时间从t0有增量△t时,质点的位置有增量 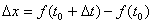 ,这就是质点在时间段△t的位移。因此,在此段时间内质点的平均速度为:
,这就是质点在时间段△t的位移。因此,在此段时间内质点的平均速度为: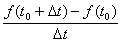 .若质点是匀速运动的则这就是在t0的瞬时速度,若质点是非匀速直线运动,则这还不是质点在t0时的瞬时速度。我们认为当时间段△t无限地接近于0时,此平均速度会无限地接近于质点t0时的瞬时速度,即:质点在t0时的瞬时速度=
.若质点是匀速运动的则这就是在t0的瞬时速度,若质点是非匀速直线运动,则这还不是质点在t0时的瞬时速度。我们认为当时间段△t无限地接近于0时,此平均速度会无限地接近于质点t0时的瞬时速度,即:质点在t0时的瞬时速度=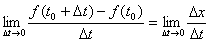 为此就产生了导数的定义,如下:
为此就产生了导数的定义,如下:
导数的定义:设函数 在点x0的某一邻域内有定义,当自变量x在x0处有增量△x(x+△x也在该邻域内)时,相应地函数有增量
在点x0的某一邻域内有定义,当自变量x在x0处有增量△x(x+△x也在该邻域内)时,相应地函数有增量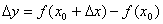 ,若△y与△x之比当△x→0时极限存在,则称这个极限值为
,若△y与△x之比当△x→0时极限存在,则称这个极限值为 在x0处的导数。记为:
在x0处的导数。记为: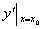 还可记为:
还可记为: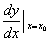 ,
,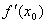
函数 在点x0处存在导数简称函数
在点x0处存在导数简称函数 在点x0处可导,否则不可导。若函数
在点x0处可导,否则不可导。若函数 在区间(a,b)内每一点都可导,就称函数
在区间(a,b)内每一点都可导,就称函数 在区间(a,b)内可导。这时函数
在区间(a,b)内可导。这时函数 对于区间(a,b)内的每一个确定的x值,都对应着一个确定的导数,这就构成一个新的函数,我们就称这个函数为原来函数
对于区间(a,b)内的每一个确定的x值,都对应着一个确定的导数,这就构成一个新的函数,我们就称这个函数为原来函数 的导函数。
注:导数也就是差商的极限
的导函数。
注:导数也就是差商的极限
左、右导数
前面我们有了左、右极限的概念,导数是差商的极限,因此我们可以给出左、右导数的概念。若极限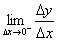 存在,我们就称它为函数
存在,我们就称它为函数 在x=x0处的左导数。若极限
在x=x0处的左导数。若极限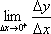 存在,我们就称它为函数
存在,我们就称它为函数 在x=x0处的右导数。
在x=x0处的右导数。
注:函数 在x0处的左右导数存在且相等是函数
在x0处的左右导数存在且相等是函数 在x0处的可导的充分必要条件
在x0处的可导的充分必要条件
函数的和、差求导法则
函数的和差求导法则
法则:两个可导函数的和(差)的导数等于这两个函数的导数的和(差).用公式可写为: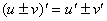 。其中u、v为可导函数。
。其中u、v为可导函数。
例题:已知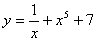 ,求
,求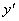
解答: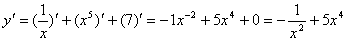
例题:已知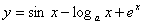 ,求
,求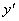
解答: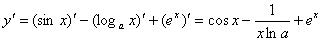
函数的积商求导法则
常数与函数的积的求导法则
法则:在求一个常数与一个可导函数的乘积的导数时,常数因子可以提到求导记号外面去。用公式可写成:
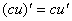
例题:已知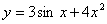 ,求
,求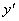
解答: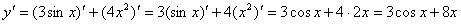
函数的积的求导法则
法则:两个可导函数乘积的导数等于第一个因子的导数乘第二个因子,加上第一个因子乘第二个因子的导数。用公式可写成: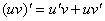
例题:已知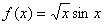 ,求
,求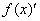
解答: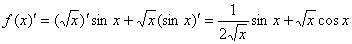
注:若是三个函数相乘,则先把其中的两个看成一项。
函数的商的求导法则
法则:两个可导函数之商的导数等于分子的导数与分母导数乘积减去分母导数与分子导数的乘积,在除以分母导数的平方。用公式可写成:
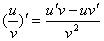
例题:已知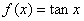 ,求
,求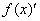
解答:
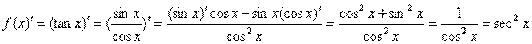
复合函数的求导法则
在学习此法则之前我们先来看一个例子!
例题:求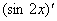 =?
=?
解答:由于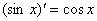 ,故
,故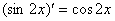 这个解答正确吗?
这个解答正确吗?
这个解答是错误的,正确的解答应该如下:
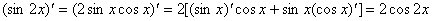
我们发生错误的原因是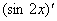 是对自变量x求导,而不是对2x求导。
是对自变量x求导,而不是对2x求导。
下面我们给出复合函数的求导法则
复合函数的求导规则
规则:两个可导函数复合而成的复合函数的导数等于函数对中间变量的导数乘上中间变量对自变量的导数。用公式表示为:
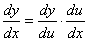 ,其中u为中间变量
,其中u为中间变量
例题:已知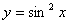 ,求
,求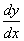
解答:设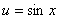 ,则
,则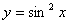 可分解为
可分解为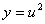 ,
,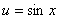 因此
因此
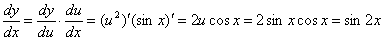
注:在以后解题中,我们可以中间步骤省去。
例题:已知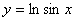 ,求
,求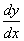 解答:
解答: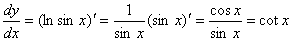
反函数求导法则
根据反函数的定义,函数 为单调连续函数,则它的反函数
为单调连续函数,则它的反函数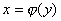 ,它也是单调连续的.为此我们可给出反函数的求导法则,如下(我们以定理的形式给出):
,它也是单调连续的.为此我们可给出反函数的求导法则,如下(我们以定理的形式给出):
定理:若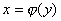 是单调连续的,且
是单调连续的,且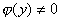 ,则它的反函数
,则它的反函数 在点x可导,且有:
在点x可导,且有: 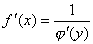 注:通过此定理我们可以发现:反函数的导数等于原函数导数的倒数。注:这里的反函数是以y为自变量的,我们没有对它作记号变换。
注:通过此定理我们可以发现:反函数的导数等于原函数导数的倒数。注:这里的反函数是以y为自变量的,我们没有对它作记号变换。
即: 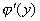 是对y求导,
是对y求导,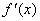 是对x求导
是对x求导
例题:求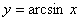 的导数.
的导数.
解答:此函数的反函数为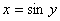 ,故
,故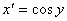 则:
则:
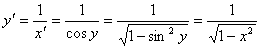
例题:求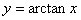 的导数.
的导数.
解答:此函数的反函数为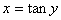 ,故
,故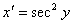 则:
则:
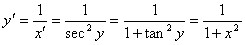
高阶导数
我们知道,在物理学上变速直线运动的速度v(t)是位置函数s(t)对时间t的导数,即: 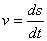 ,而加速度a又是速度v对时间t的变化率,即速度v对时间t的导数:
,而加速度a又是速度v对时间t的变化率,即速度v对时间t的导数: 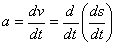 ,或
,或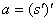 。这种导数的导数
。这种导数的导数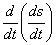 叫做s对t的二阶导数。下面我们给出它的数学定义:
叫做s对t的二阶导数。下面我们给出它的数学定义:
定义:函数 的导数
的导数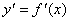 仍然是x的函数.我们把
仍然是x的函数.我们把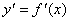 的导数叫做函数
的导数叫做函数 的二阶导数,记作
的二阶导数,记作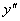 或
或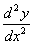 ,即:
,即: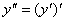 或
或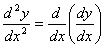 .相应地,把
.相应地,把 的导数
的导数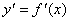 叫做函数
叫做函数 的一阶导数.类似地,二阶导数的导数,叫做三阶导数,三阶导数的导数,叫做四阶导数,…,一般地(n-1)阶导数的导数叫做n阶导数.
的一阶导数.类似地,二阶导数的导数,叫做三阶导数,三阶导数的导数,叫做四阶导数,…,一般地(n-1)阶导数的导数叫做n阶导数.
分别记作: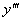 ,
,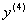 ,…,
,…,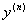 或
或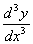 ,
,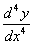 ,…,
,…,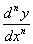
二阶及二阶以上的导数统称高阶导数。由此可见,求高阶导数就是多次接连地求导,所以,在求高阶导数时可运用前面所学的求导方法。
例题:已知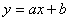 ,求
,求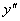 解答:因为
解答:因为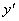 =a,故
=a,故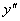 =0
=0
例题:求对数函数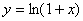 的n阶导数。
的n阶导数。
解答: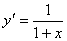 ,
,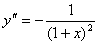 ,
,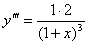 ,
,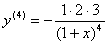 ,
,
一般地,可得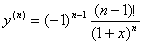
隐函数及其求导法则
我们知道用解析法表示函数,可以有不同的形式.若函数y可以用含自变量x的算式表示,像y=sinx,y=1+3x等,这样的函数叫显函数.前面我们所遇到的函数大多都是显函数.
一般地,如果方程F(x,y)=0中,令x在某一区间内任取一值时,相应地总有满足此方程的y值存在,则我们就说方程F(x,y)=0在该区间上确定了x的隐函数y.把一个隐函数化成显函数的形式,叫做隐函数的显化。注:有些隐函数并不是很容易化为显函数的,那么在求其导数时该如何呢?下面让我们来解决这个问题!
隐函数的求导
若已知F(x,y)=0,求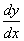 时,一般按下列步骤进行求解:
时,一般按下列步骤进行求解:
a):若方程F(x,y)=0,能化为 的形式,则用前面我们所学的方法进行求导;
的形式,则用前面我们所学的方法进行求导;
b):若方程F(x,y)=0,不能化为 的形式,则是方程两边对x进行求导,并把y看成x的函数
的形式,则是方程两边对x进行求导,并把y看成x的函数 ,用复合函数求导法则进行。
,用复合函数求导法则进行。
例题:已知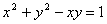 ,求
,求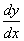
解答:此方程不易显化,故运用隐函数求导法.两边对x进行求导, 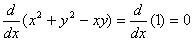 ,
,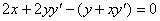 ,故
,故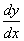 =
=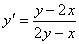 注:我们对隐函数两边对x进行求导时,一定要把变量y看成x的函数,然后对其利用复合函数求导法则进行求导。
注:我们对隐函数两边对x进行求导时,一定要把变量y看成x的函数,然后对其利用复合函数求导法则进行求导。
例题:求隐函数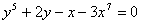 ,在x=0处的导数
,在x=0处的导数
解答:两边对x求导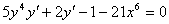 ,故
,故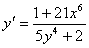 ,当x=0时,y=0.故
,当x=0时,y=0.故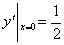 。
。
有些函数在求导数时,若对其直接求导有时很不方便,像对某些幂函数进行求导时,有没有一种比较直观的方法呢?下面我们再来学习一种求导的方法:对数求导法
对数求导法
对数求导的法则:根据隐函数求导的方法,对某一函数先取函数的自然对数,然后在求导。注:此方法特别适用于幂函数的求导问题。
例题:已知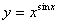 x>0,求
x>0,求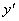
此题若对其直接求导比较麻烦,我们可以先对其两边取自然对数,然后再把它看成隐函数进行求导,就比较简便些。如下
解答:先两边取对数: 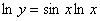 ,把其看成隐函数,再两边求导
,把其看成隐函数,再两边求导
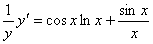
因为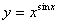 ,所以
,所以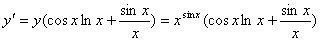
例题:已知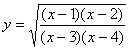 ,求
,求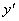
此题可用复合函数求导法则进行求导,但是比较麻烦,下面我们利用对数求导法进行求导
解答:先两边取对数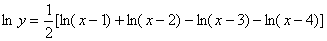 再两边求导
再两边求导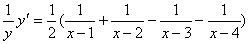 因为
因为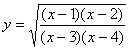 ,所以
,所以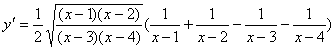
函数的微分
学习函数的微分之前,我们先来分析一个具体问题:一块正方形金属薄片受温度变化的影响时,其边长由x0变到了x0+△x,则此薄片的面积改变了多少?
解答:设此薄片的边长为x,面积为A,则A是x的函数: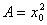 薄片受温度变化的影响面积的改变量,可以看成是当自变量x从x0取的增量△x时,函数A相应的增量△A,即:
薄片受温度变化的影响面积的改变量,可以看成是当自变量x从x0取的增量△x时,函数A相应的增量△A,即: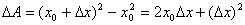 。从上式我们可以看出,△A分成两部分,第一部分
。从上式我们可以看出,△A分成两部分,第一部分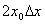 是△x的线性函数,即下图中红色部分;第二部分
是△x的线性函数,即下图中红色部分;第二部分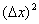 即图中的黑色部分,
即图中的黑色部分,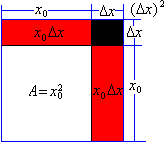 当△x→0时,它是△x的高阶无穷小,表示为:
当△x→0时,它是△x的高阶无穷小,表示为: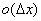
由此我们可以发现,如果边长变化的很小时,面积的改变量可以近似的用地一部分来代替。下面我们给出微分的数学定义:
函数微分的定义:设函数在某区间内有定义,x0及x0+△x在这区间内,若函数的增量可表示为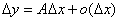 ,其中A是不依赖于△x的常数,
,其中A是不依赖于△x的常数,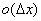 是△x的高阶无穷小,则称函数
是△x的高阶无穷小,则称函数 在点x0可微的。
在点x0可微的。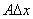 叫做函数
叫做函数 在点x0相应于自变量增量△x的微分,记作dy,即:
在点x0相应于自变量增量△x的微分,记作dy,即: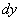 =
=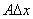 。
。
通过上面的学习我们知道:微分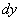 是自变量改变量△x的线性函数,dy与△y的差
是自变量改变量△x的线性函数,dy与△y的差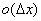 是关于△x的高阶无穷小量,我们把dy称作△y的线性主部。于是我们又得出:当△x→0时,△y≈dy.导数的记号为:
是关于△x的高阶无穷小量,我们把dy称作△y的线性主部。于是我们又得出:当△x→0时,△y≈dy.导数的记号为: 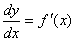 ,现在我们可以发现,它不仅表示导数的记号,而且还可以表示两个微分的比值(把△x看成dx,即:定义自变量的增量等于自变量的微分),还可表示为:
,现在我们可以发现,它不仅表示导数的记号,而且还可以表示两个微分的比值(把△x看成dx,即:定义自变量的增量等于自变量的微分),还可表示为:
由此我们得出:若函数在某区间上可导,则它在此区间上一定可微,反之亦成立。
微分形式不变性
什么是微分形式不边形呢?
设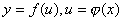 ,则复合函数 ,则复合函数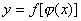 的微分为: 的微分为:
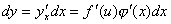 ,
由于 ,
由于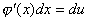 ,故我们可以把复合函数的微分写成 ,故我们可以把复合函数的微分写成
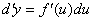 由此可见,不论u是自变量还是中间变量,
由此可见,不论u是自变量还是中间变量,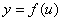 的微分dy总可以用 的微分dy总可以用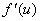 与du的乘积来表示,
我们把这一性质称为微分形式不变性。
例题:已知 与du的乘积来表示,
我们把这一性质称为微分形式不变性。
例题:已知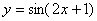 ,求dy
解答:把2x+1看成中间变量u,根据微分形式不变性,则 ,求dy
解答:把2x+1看成中间变量u,根据微分形式不变性,则
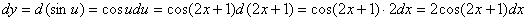 |
||||||||||||||
|
通过上面的学习,我们知道微分与导数有着不可分割的联系,前面我们知道基本初等函数的导数公式和导数
的运算法则,那么基本初等函数的微分公式和微分运算法则是怎样的呢?
下面我们来学习---基本初等函数的微分公式与微分的运算法则 |
||||||||||||||
|
基本初等函数的微分公式与微分的运算法则 |
||||||||||||||
基本初等函数的微分公式
由于函数微分的表达式为: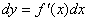 ,于是我们通过基本初等函数导数的公式可得出基本初等函数微分的公式,下面我们用表格来把基本初等函数的导数公式与微分公式对比一下:(部分公式) ,于是我们通过基本初等函数导数的公式可得出基本初等函数微分的公式,下面我们用表格来把基本初等函数的导数公式与微分公式对比一下:(部分公式)
|
||||||||||||||
微分运算法则
由函数和、差、积、商的求导法则,可推出相应的微分法则.为了便于理解,下面我们用表格来把微分的运算法则与导数的运算法则对照一下:
|
||||||||||||||
|
复合函数的微分法则就是前面我们学到的微分形式不变性,在此不再详述。 |
||||||||||||||
例题:设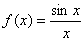 ,求 ,求 对x3的导数
解答:根据微分形式的不变性 对x3的导数
解答:根据微分形式的不变性
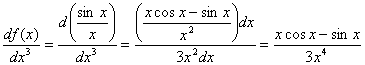 |
||||||||||||||
微分的应用
微分是表示函数增量的线性主部.计算函数的增量,有时比较困难,但计算微分则比较简单,为此我们用函数的微分来近似的代替函数的增量,这就是微分在近似计算中的应用.
例题:求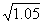 的近似值。
解答:我们发现用计算的方法特别麻烦,为此把转化为求微分的问题 的近似值。
解答:我们发现用计算的方法特别麻烦,为此把转化为求微分的问题
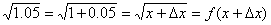
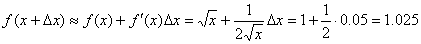 故其近似值为1.025(精确值为1.024695)
故其近似值为1.025(精确值为1.024695) |
10、函数极限的运算规则
前面已经学习了数列极限的运算规则,我们知道数列可作为一类特殊的函数,故函数极限的运算规则与数列极限的运算规则相似。
⑴、函数极限的运算规则
若已知x→x0(或x→∞)时,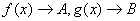 .
.
则: 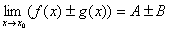
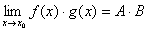
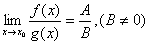
推论: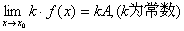
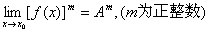
在求函数的极限时,利用上述规则就可把一个复杂的函数化为若干个简单的函数来求极限。
例题:求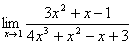
解答: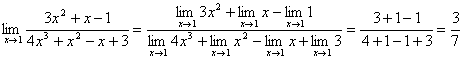
例题:求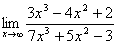
此题如果像上题那样求解,则会发现此函数的极限不存在.我们通过观察可以发现此分式的分子和分母都没有极限,像这种情况怎么办呢?下面我们把它解出来。
解答: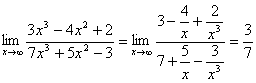
注:通过此例题我们可以发现:当分式的分子和分母都没有极限时就不能运用商的极限的运算规则了,应先把分式的分子分母转化为存在极限的情形,然后运用规则求之。
函数极限的存在准则
学习函数极限的存在准则之前,我们先来学习一下左、右的概念。
我们先来看一个例子:
例:符号函数为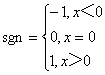
对于这个分段函数,x从左趋于0和从右趋于0时函数极限是不相同的.为此我们定义了左、右极限的概念。
定义:如果x仅从左侧(x<x0)趋近x0时,函数 与常量A无限接近,则称A为函数
与常量A无限接近,则称A为函数 当
当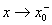 时的左极限.记:
时的左极限.记: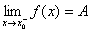
如果x仅从右侧(x>x0)趋近x0时,函数 与常量A无限接近,则称A为函数
与常量A无限接近,则称A为函数 当
当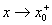 时的右极限.记:
时的右极限.记: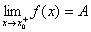
注:只有当x→x0时,函数 的左、右极限存在且相等,方称
的左、右极限存在且相等,方称 在x→x0时有极限
在x→x0时有极限
函数极限的存在准则
准则一:对于点x0的某一邻域内的一切x,x0点本身可以除外(或绝对值大于某一正数的一切x)有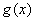 ≤
≤ ≤
≤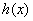 ,且
,且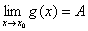 ,
,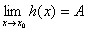
那末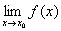 存在,且等于A
存在,且等于A
注:此准则也就是夹逼准则.
准则二:单调有界的函数必有极限.
注:有极限的函数不一定单调有界
两个重要的极限
一: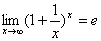
注:其中e为无理数,它的值为:e=2.718281828459045...
二: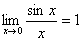
注:在此我们对这两个重要极限不加以证明.
注:我们要牢记这两个重要极限,在今后的解题中会经常用到它们.
例题:求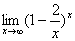
解答:令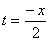 ,则x=-2t,因为x→∞,故t→∞,
,则x=-2t,因为x→∞,故t→∞,
则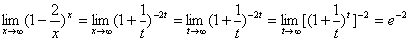
注:解此类型的题时,一定要注意代换后的变量的趋向情况,象x→∞时,若用t代换1/x,则t→0.
无穷大量和无穷小量
无穷大量
我们先来看一个例子:
已知函数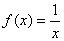 ,当x→0时,可知
,当x→0时,可知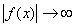 ,我们把这种情况称为
,我们把这种情况称为 趋向无穷大。为此我们可定义如下:设有函数y=
趋向无穷大。为此我们可定义如下:设有函数y= ,在x=x0的去心邻域内有定义,对于任意给定的正数N(一个任意大的数),总可找到正数δ,当
,在x=x0的去心邻域内有定义,对于任意给定的正数N(一个任意大的数),总可找到正数δ,当
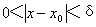 时,
时,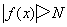 成立,则称函数当
成立,则称函数当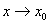 时为无穷大量。
时为无穷大量。
记为: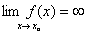 (表示为无穷大量,实际它是没有极限的)
(表示为无穷大量,实际它是没有极限的)
同样我们可以给出当x→∞时, 无限趋大的定义:设有函数y=
无限趋大的定义:设有函数y= ,当x充分大时有定义,对于任意给定的正数N(一个任意大的数),总可以找到正数M,当
,当x充分大时有定义,对于任意给定的正数N(一个任意大的数),总可以找到正数M,当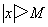 时,
时,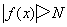 成立,则称函数当x→∞时是无穷大量,记为:
成立,则称函数当x→∞时是无穷大量,记为: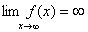
无穷小量
以零为极限的变量称为无穷小量。
定义:设有函数 ,对于任意给定的正数ε(不论它多么小),总存在正数δ(或正数M),使得对于适合不等式
,对于任意给定的正数ε(不论它多么小),总存在正数δ(或正数M),使得对于适合不等式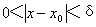 (或
(或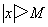 )的一切x,所对应的函数值满足不等式
)的一切x,所对应的函数值满足不等式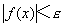 ,则称函数
,则称函数 当
当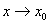 (或x→∞)时 为无穷小量.
(或x→∞)时 为无穷小量.
记作: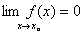 (或
(或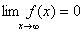 )
)
注意:无穷大量与无穷小量都是一个变化不定的量,不是常量,只有0可作为无穷小量的唯一常量。无穷大量与无穷小量的区别是:前者无界,后者有界,前者发散,后者收敛于0.无穷大量与无穷小量是互为倒数关系的.
关于无穷小量的两个定理
定理一:如果函数 在
在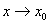 (或x→∞)时有极限A,则差
(或x→∞)时有极限A,则差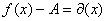 是当
是当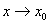 (或x→∞)时的无穷小量,反之亦成立。
(或x→∞)时的无穷小量,反之亦成立。
定理二:无穷小量的有利运算定理
a):有限个无穷小量的代数和仍是无穷小量; b):有限个无穷小量的积仍是无穷小量;c):常数与无穷小量的积也是无穷小量.
无穷小量的比较
通过前面的学习我们已经知道,两个无穷小量的和、差及乘积仍旧是无穷小.那么两个无穷小量的商会是怎样的呢?好!接下来我们就来解决这个问题,这就是我们要学的两个无穷小量的比较。
定义:设α,β都是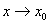 时的无穷小量,且β在x0的去心领域内不为零,
时的无穷小量,且β在x0的去心领域内不为零,
a):如果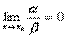 ,则称α是β的高阶无穷小或β是α的低阶无穷小;
,则称α是β的高阶无穷小或β是α的低阶无穷小;
b):如果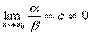 ,则称α和β是同阶无穷小;
,则称α和β是同阶无穷小;
c):如果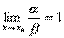 ,则称α和β是等价无穷小,记作:α∽β(α与β等价)
,则称α和β是等价无穷小,记作:α∽β(α与β等价)
例:因为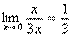 ,所以当x→0时,x与3x是同阶无穷小;
,所以当x→0时,x与3x是同阶无穷小;
因为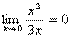 ,所以当x→0时,x2是3x的高阶无穷小;
,所以当x→0时,x2是3x的高阶无穷小;
因为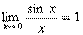 ,所以当x→0时,sinx与x是等价无穷小。
,所以当x→0时,sinx与x是等价无穷小。
等价无穷小的性质
设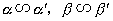 ,且
,且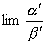 存在,则
存在,则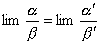 .
.
注:这个性质表明:求两个无穷小之比的极限时,分子及分母都可用等价无穷小来代替,因此我们可以利用这个性质来简化求极限问题。
例题:1.求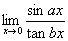 解答:当x→0时,sinax∽ax,tanbx∽bx,故:
解答:当x→0时,sinax∽ax,tanbx∽bx,故: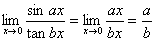
例题: 2.求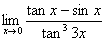
解答: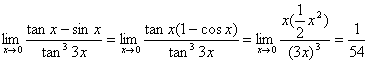
注: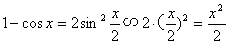
注:从这个例题中我们可以发现,作无穷小变换时,要代换式中的某一项,不能只代换某个因子。
函数的一重要性质--连续性
在自然界中有许多现象,如气温的变化,植物的生长等都是连续地变化着的.这种现象在函数关系上的反映,就是函数的连续性
在定义函数的连续性之前我们先来学习一个概念--增量
设变量x从它的一个初值x1变到终值x2,终值与初值的差x2-x1就叫做变量x的增量,记为:△x即:△x=x2-x1 增量△x可正可负.
我们再来看一个例子:函数 在点x0的邻域内有定义,当自变量x在领域内从x0变到x0+△x时,函数y相应地从
在点x0的邻域内有定义,当自变量x在领域内从x0变到x0+△x时,函数y相应地从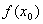 变到
变到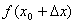 ,其对应的增量为:
,其对应的增量为:
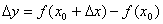
这个关系式的几何解释如下图: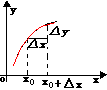
现在我们可对连续性的概念这样描述:如果当△x趋向于零时,函数y对应的增量△y也趋向于零,即: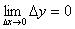 ,那末就称函数
,那末就称函数 在点x0处连续。
在点x0处连续。
函数连续性的定义:
设函数 在点x0的某个邻域内有定义,如果有
在点x0的某个邻域内有定义,如果有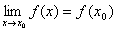 称函数
称函数 在点x0处连续,且称x0为函数的
在点x0处连续,且称x0为函数的 的连续点.
的连续点.
下面我们结合着函数左、右极限的概念再来学习一下函数左、右连续的概念:设函数 在区间(a,b]内有定义,如果左极限
在区间(a,b]内有定义,如果左极限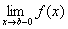 存在且等于
存在且等于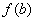 ,即:
,即: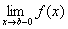 =
=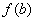 ,那末我们就称函数
,那末我们就称函数 在点b左连续.设函数
在点b左连续.设函数 在区间[a,b)内有定义,如果右极限
在区间[a,b)内有定义,如果右极限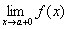 存在且等于
存在且等于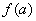 ,即:
,即: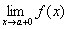 =
=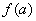 ,那末我们就称函数
,那末我们就称函数 在点a右连续.
在点a右连续.
一个函数在开区间(a,b)内每点连续,则为在(a,b)连续,若又在a点右连续,b点左连续,则在闭区间[a,b]连续,如果在整个定义域内连续,则称为连续函数。
注:一个函数若在定义域内某一点左、右都连续,则称函数在此点连续,否则在此点不连续.
注:连续函数图形是一条连续而不间断的曲线。
通过上面的学习我们已经知道函数的连续性了,同时我们可以想到若函数在某一点要是不连续会出现什么情形呢?接着我们就来学习这个问题:函数的间断点
函数的间断点
定义:我们把不满足函数连续性的点称之为间断点.
|
它包括三种情形: |
a): 在x0无定义; 在x0无定义; |
|
|
b): 在x→x0时无极限; 在x→x0时无极限; |
|
|
c): 在x→x0时有极限但不等于 在x→x0时有极限但不等于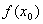 ; ; |
下面我们通过例题来学习一下间断点的类型:
例1: 正切函数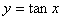 在
在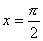 处没有定义,所以点
处没有定义,所以点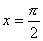 是函数
是函数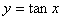 的间断点,因
的间断点,因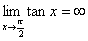 ,我们就称
,我们就称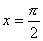 为函数
为函数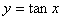 的无穷间断点;
的无穷间断点;
例2:函数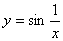 在点x=0处没有定义;故当x→0时,函数值在-1与+1之间变动无限多次,我们就称点x=0叫做函数
在点x=0处没有定义;故当x→0时,函数值在-1与+1之间变动无限多次,我们就称点x=0叫做函数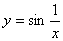 的振荡间断点;
例3:函数
的振荡间断点;
例3:函数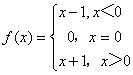 当x→0时,左极限
当x→0时,左极限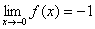 ,右极限
,右极限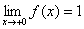 ,从这我们可以看出函数左、右极限虽然都存在,但不相等,故函数在点x=0是不存在极限。我们还可以发现在点x=0时,函数值产生跳跃现象,为此我们把这种间断点称为跳跃间断点;我们把上述三种间断点用几何图形表示出来如下:
,从这我们可以看出函数左、右极限虽然都存在,但不相等,故函数在点x=0是不存在极限。我们还可以发现在点x=0时,函数值产生跳跃现象,为此我们把这种间断点称为跳跃间断点;我们把上述三种间断点用几何图形表示出来如下:
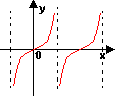
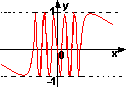
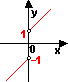
间断点的分类
我们通常把间断点分成两类:如果x0是函数 的间断点,且其左、右极限都存在,我们把x0称为函数
的间断点,且其左、右极限都存在,我们把x0称为函数 的第一类间断点;不是第一类间断点的任何间断点,称为第二类间断点.
的第一类间断点;不是第一类间断点的任何间断点,称为第二类间断点.
可去间断点
若x0是函数 的间断点,但极限
的间断点,但极限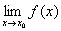 存在,那末x0是函数
存在,那末x0是函数 的第一类间断点。此时函数不连续原因是:
的第一类间断点。此时函数不连续原因是: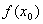 不存在或者是存在但
不存在或者是存在但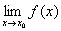 ≠
≠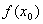 。我们令
。我们令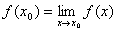 ,则可使函数
,则可使函数 在点x0处连续,故这种间断点x0称为可去间断点。
在点x0处连续,故这种间断点x0称为可去间断点。
连续函数的性质及初等函数的连续性
连续函数的性质
函数的和、积、商的连续性
我们通过函数在某点连续的定义和极限的四则运算法则,可得出以下结论:
a):有限个在某点连续的函数的和是一个在该点连续的函数;
b):有限个在某点连续的函数的乘积是一个在该点连续的函数;
c):两个在某点连续的函数的商是一个在该点连续的函数(分母在该点不为零);
反函数的连续性
若函数 在某区间上单调增(或单调减)且连续,那末它的反函数
在某区间上单调增(或单调减)且连续,那末它的反函数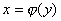 也在对应的区间上单调增(单调减)且连续
也在对应的区间上单调增(单调减)且连续
例:函数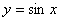 在闭区间
在闭区间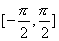 上单调增且连续,故它的反函数
上单调增且连续,故它的反函数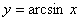 在闭区间[-1,1]上也是单调增且连续的。
在闭区间[-1,1]上也是单调增且连续的。
复合函数的连续性
设函数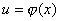 当x→x0时的极限存在且等于a,即:
当x→x0时的极限存在且等于a,即: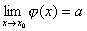 .而函数
.而函数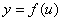 在点u=a连续,那末复合函数
在点u=a连续,那末复合函数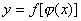 当x→x0时的极限也存在且等于
当x→x0时的极限也存在且等于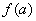 .即:
.即: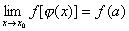
例题:求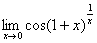
解答: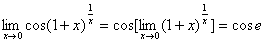
注:函数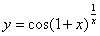 可看作
可看作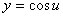 与
与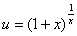 复合而成,且函数
复合而成,且函数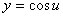 在点u=e连续,因此可得出上述结论。
在点u=e连续,因此可得出上述结论。
设函数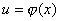 在点x=x0连续,且
在点x=x0连续,且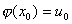 ,而函数
,而函数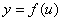 在点u=u0连续,那末复合函数
在点u=u0连续,那末复合函数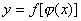 在点x=x0也是连续的
在点x=x0也是连续的
初等函数的连续性
通过前面我们所学的概念和性质,我们可得出以下结论:基本初等函数在它们的定义域内都是连续的;一切初等函数在其定义域内也都是连续的.
闭区间上连续函数的性质
闭区间上的连续函数则是在其连续区间的左端点右连续,右端点左连续.对于闭区间上的连续函数有几条重要的性质,下面我们来学习一下: 最大值最小值定理:在闭区间上连续的函数一定有最大值和最小值。(在此不作证明) 例:函数y=sinx在闭区间[0,2π]上连续,则在点x=π/2处,它的函数值为1,且大于闭区间[0,2π]上其它各点出的函数值;则在点x=3π/2处,它的函数值为-1,且小于闭区间[0,2π]上其它各点出的函数值。
介值定理 在闭区间上连续的函数一定取得介于区间两端点的函数值间的任何值。即: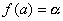
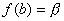 ,μ在α、β之间,则在[a,b]间一定有一个ξ,使
,μ在α、β之间,则在[a,b]间一定有一个ξ,使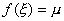 推论: 在闭区间连续的函数必取得介于最大值最小值之间的任何值。
推论: 在闭区间连续的函数必取得介于最大值最小值之间的任何值。
9、函数的极限
前面我们学习了数列的极限,已经知道数列可看作一类特殊的函数,即自变量取 1→∞内的正整数,若自变量不再限于正整数的顺序,而是连续变化的,就成了函数。下面我们来学习函数的极限.
函数的极值有两种情况:a):自变量无限增大;b):自变量无限接近某一定点x0,如果在这时,函数值无限接近于某一常数A,就叫做函数存在极值。我们已知道函数的极值的情况,那么函数的极限如何呢 ?
下面我们结合着数列的极限来学习一下函数极限的概念!
⑴、函数的极限(分两种情况)
a):自变量趋向无穷大时函数的极限
定义:设函数 ,若对于任意给定的正数ε(不论其多么小),总存在着正数X,使得对于适合不等式
,若对于任意给定的正数ε(不论其多么小),总存在着正数X,使得对于适合不等式 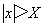 的一切x,所对应的函数值
的一切x,所对应的函数值 都满足不等式
都满足不等式
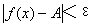
那末常数A就叫做函数 当x→∞时的极限,记作:
当x→∞时的极限,记作: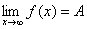
下面我们用表格把函数的极限与数列的极限对比一下:
|
数列的极限的定义 |
函数的极限的定义 |
存在数列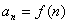 与常数A,任给一正数ε>0,总可找到一正整数N,对于n>N的所有 与常数A,任给一正数ε>0,总可找到一正整数N,对于n>N的所有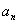 都满足 都满足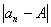 <ε则称数列 <ε则称数列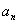 ,当x→∞时收敛于A记: ,当x→∞时收敛于A记: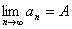 。 。 |
存在函数 与常数A,任给一正数ε>0,总可找到一正数X,对于适合 与常数A,任给一正数ε>0,总可找到一正数X,对于适合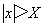 的一切x,都满足 的一切x,都满足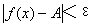 ,函数 ,函数 当x→∞时的极限为A,记: 当x→∞时的极限为A,记: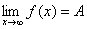 。 。 |
 |
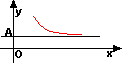 |
从上表我们发现了什么 ??试思考之
b):自变量趋向有限值时函数的极限。我们先来看一个例子.
例:函数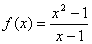 ,当x→1时函数值的变化趋势如何?函数在x=1处无定义.我们知道对实数来讲,在数轴上任何一个有限的范围内,都有无穷多个点,为此我们把x→1时函数值的变化趋势用表列出,如下图:
,当x→1时函数值的变化趋势如何?函数在x=1处无定义.我们知道对实数来讲,在数轴上任何一个有限的范围内,都有无穷多个点,为此我们把x→1时函数值的变化趋势用表列出,如下图:
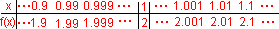
从中我们可以看出x→1时, →2.而且只要x与1有多接近,
→2.而且只要x与1有多接近, 就与2有多接近.或说:只要
就与2有多接近.或说:只要 与2只差一个微量ε,就一定可以找到一个δ,当
与2只差一个微量ε,就一定可以找到一个δ,当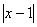 <δ时满足
<δ时满足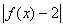 <δ定义:设函数
<δ定义:设函数 在某点x0的某个去心邻域内有定义,且存在数A,如果对任意给定的ε(不论其多么小),总存在正数δ,当0<
在某点x0的某个去心邻域内有定义,且存在数A,如果对任意给定的ε(不论其多么小),总存在正数δ,当0<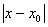 <δ时,
<δ时,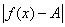 <ε则称函数
<ε则称函数 当x→x0时存在极限,且极限为A,记:
当x→x0时存在极限,且极限为A,记: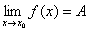 。
。
注:在定义中为什么是在去心邻域内呢?这是因为我们只讨论x→x0的过程,与x=x0出的情况无关。此定义的核心问题是:对给出的ε,是否存在正数δ,使其在去心邻域内的x均满足不等式。
有些时候,我们要用此极限的定义来证明函数的极限为 A,其证明方法是怎样的呢?
a):先任取ε>0;
b):写出不等式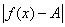 <ε;
c):解不等式能否得出去心邻域0<
<ε;
c):解不等式能否得出去心邻域0<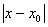 <δ,若能;
d):则对于任给的ε>0,总能找出δ,当0<
<δ,若能;
d):则对于任给的ε>0,总能找出δ,当0<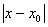 <δ时,
<δ时,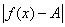 <ε成立,因此
<ε成立,因此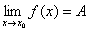
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com