
3.(本小题满分14分)
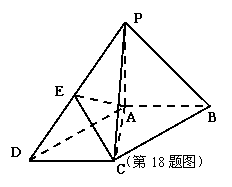 如图,在底面为平行四边形的四棱锥
如图,在底面为平行四边形的四棱锥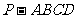 中,
中,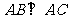 ,
,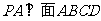 ,点
,点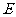 是
是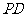 的中点。
的中点。
(1)求证: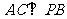 ;
;
(2)求证: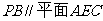
2.(本小题满分12分)某高校在2009年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如下左图所示.
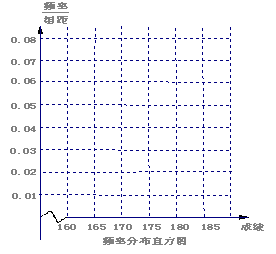
(1)请先求出频率分布表中①、②位置相应数据,再在答题纸上完成下列频率分布直方图;
(2)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试?
(3)在(2)的前提下,学校决定在6名学生中随机抽取2名学生接受A考官进行面试,求:第4组至少有一名学生被考官A面试的概率?
|
组号 |
分组 |
频数 |
频率 |
|
第1组 |
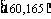 |
5 |
0.050 |
|
第2组 |
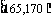 |
① |
0.350 |
|
第3组 |
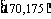 |
30 |
② |
|
第4组 |
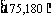 |
20 |
0.200 |
|
第5组 |
 |
10 |
0.100 |
|
合计 |
100 |
1.00 |
3.(本题满分14分)
已知关于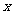 的一元二次函数
的一元二次函数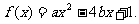
(Ⅰ)设集合P={1,2, 3}和Q={-1,1,2,3,4},分别从集合P和Q中随机取一个数作
为 和
和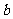 ,求函数
,求函数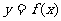 在区间[
在区间[ 上是增函数的概率;
上是增函数的概率;
(Ⅱ)设点( ,
,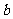 )是区域
)是区域 内的随机点,求函数
内的随机点,求函数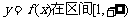 上是增函数的概率.
1.(本题满分14分,第1小题5分,第2小题9分)
上是增函数的概率.
1.(本题满分14分,第1小题5分,第2小题9分)
已知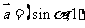 ,
,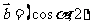 ,
,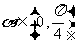 .
.
⑴若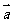 ∥
∥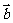 ,求
,求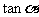 的值;
的值;
⑵若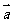
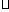
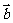
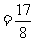 ,求
,求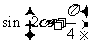 的值.
的值.
2. (本小题12分)
(本小题12分)
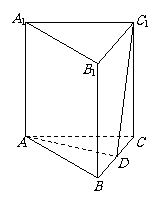
如图,在正三棱柱ABC-A1B1C1中,点D在边BC上,AD⊥C1D.
(1)求证:AD⊥平面BC C1 B1;
(2)设E是B1C1上的一点,当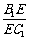 的值为多少时,
的值为多少时,
A1E∥平面ADC1?请给出证明.
1.(本小题12分)
在△ 中,角, ,
中,角, ,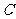 的对边分别为,
的对边分别为,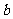 ,.已知
,.已知
向量 ,
,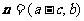 ,且
,且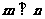 .
.
(1)求角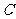 的大小;
的大小;
(2)若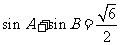 ,求角的值。
,求角的值。
3.(本小题满分14分)
如图,在直三棱柱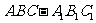 中,
中,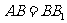 ,
,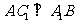 ,
,
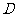 为
为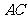 的中点.
的中点.
(Ⅰ)求证: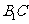 ∥平面
∥平面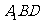 ;
;
(Ⅱ)求证:平面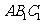 ⊥平面
⊥平面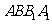 .
.
2.(本小题满分12分)
已知函数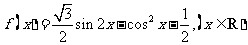 .
.
(I)求函数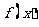 的最小值和最小正周期;
的最小值和最小正周期;
(II)设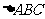 的内角
的内角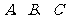 的对边分别为
的对边分别为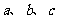 ,且
,且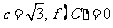 ,若向量
,若向量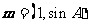 与向量
与向量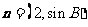 共线,求
共线,求 的值.
的值.
1.(本小题满分12分)
甲、乙两人共同抛掷一枚硬币,规定硬币正面朝上甲得1分,否则乙得1分,先积得3分者获胜,并结束游戏。
(I)求在前3次抛掷中甲得2分,乙得1分的概率;
(II)若甲已经积得2分,乙已经积得1分,求甲最终获胜的概率。
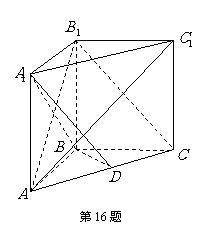
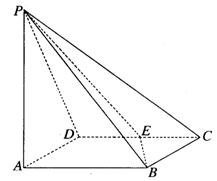
4.(本题满分12分)如图,四棱锥P-ABCD的底面ABCD是边长为1的菱形,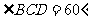 ,E是CD的中点,
,E是CD的中点,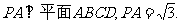
(Ⅰ)证明:平面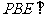 平面PAB;
平面PAB;
(Ⅱ)求二面角A-BE-P的大小。
3.已知集合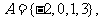 在平面直角坐标系中,点M(x,y)的坐标
在平面直角坐标系中,点M(x,y)的坐标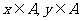 。
。
(Ⅰ)请列出点M的所有坐标;
(Ⅱ)求点M不在y轴上的概率;
 (Ⅲ)求点M正好落在区域
(Ⅲ)求点M正好落在区域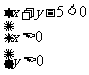 上的概率。
上的概率。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com