请考生在第22、23、24题中任选一题做答，如果多做，则按所做的第一题记分．

做答时，用2B铅笔在答题卡上把所选题目对应的题号涂黑．

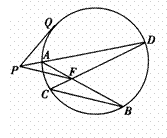
22．选修4－1：几何证明选讲

圆的两条弦AB、CD交于点F，从F点引BC的平行线和直线

DA的延长线交于点P，再从点P引这个圆的切线，切点是Q.

求证：PF=PQ.

21．(本小题满分12分)

已知函数f(x)是定义在[-e,0)∪(0,e]上的奇函数，当x∈(0,e],f(x)=ax+lnx(其中e是自然对数的底，a∈R)

(1)求f(x)的解析式；

(2)设g(x)=,x∈[-e,0),求证：当a=-1时，f(x)>g(x)+;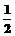

(3)是否存在实数a，使得当x∈[-e,0)时f(x)的最小值是3？如果存在，求出实数a的值；如果不存在，请说明理由。

20．(本小题满分12分)

在平面直角坐标系xoy中，已知以O为圆心的圆与直线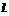：y=mx+(3-4m)(m∈R)恒有公共点，且要求使圆O的面积最小。

(1)证明直线过定点M，求出此点的坐标及圆O的方程；

(2)已知定点Q(-4,3)，直线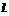与圆O交于M、N两点，试判断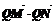×tan∠MQN是否有最大值，若存在求出最大值，并求出此时直线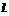的方程，若不存在，给出理由。

(3)圆O与x轴相交于A、B两点，圆内动点P使|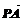|、||、||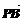成等比数列，求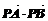的范围。

19．(本小题满分12分)

有一种舞台灯，外形是正六棱柱，在其每一个侧面(编号为①②③④⑤⑥)上安装5只颜色各异的灯，假若每只灯正常发光的概率为0.5，若一个侧面上至少有3只灯发光，则不需要更换这个面，否则需要更换这个面，假定更换一个面需要100元，用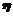表示更换的面数，用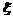表示更换费用。

(1)求①号面需要更换的概率；

(2)求6个面中恰好有2个面需要更换的概率；

(3)写出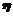的分布列，求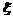的数学期望。

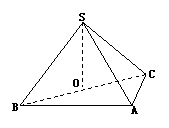
18．(理)(本小题满分12分)

如图，在三棱锥S-ABC中，侧面SAB与侧面SAC

均为等边三角形，∠BAC=90°，O为BC的中点。

(1)证明：SO⊥平面ABC；

(2)求二面角A-SC-B的余弦值.

17．(本小题满分12分)

已知向量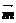=(sin2x,cosx),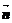=(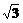,2cosx)(x∈R),f(x)=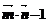

(1)求f(x)的单调递增区间；

(2)在△ABC中，角A、B、C的对边分别为a,b,c，f(A)=2,a=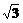,B=,求b的值。

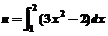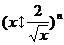16．设，则展开式中含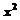项的系数是_________。

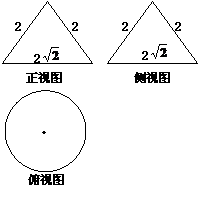
15．一个几何体的三视图如下图所示，

则该几何体外接球的表面积为_______。

14．将全体正整数排成一个三角形数阵

1

2　　　 3

4　　　 5　　　 6

7　　 8　　　 9　　　 10

11　 12　　 13　　 14　　　 15

…　…　…　…　…　…　…　…　…

根据以上排列规律，数阵中第n(n≥3)行的

从左至右的第3个数是_______。

13．已知向量=(sin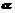,2)与向量=(cos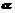,1)互相平行，则tan2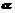的值为_______。