
4.解:点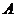 和点
和点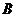 分别在直线
分别在直线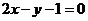 和直线
和直线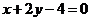 上,
上,
可设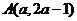 ,
,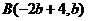 ,而
,而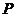 为线段
为线段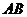 的中点,
的中点,
则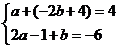 ,得
,得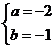 ,即
,即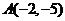 ,
,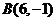 ,
,
得直线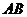 的方程为
的方程为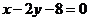 .
.
4.已知一条直线过点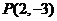 ,与直线
,与直线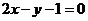 和直线
和直线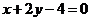 分别相交于
分别相交于
点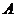 和点
和点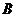 ,且
,且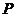 为线段
为线段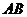 的中点,求这条直线的方程.
的中点,求这条直线的方程.
3.解:因为直线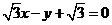 的斜率为
的斜率为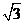 ,
,
所以直线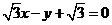 的倾斜角为
的倾斜角为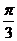 ,得所求直线的倾斜角为
,得所求直线的倾斜角为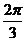 ,
,
即所求直线的斜率为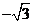 ,则
,则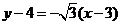 ,
,
即直线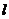 的方程为
的方程为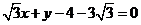 .
.
3.直线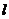 经过点
经过点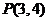 ,它的倾斜角是直线
,它的倾斜角是直线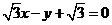 的倾斜角
的倾斜角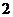 倍,
倍,
求直线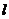 的方程.
的方程.
2.填空题
(1)直线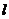 过点
过点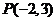 ,且与
,且与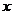 轴、
轴、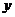 轴分别交于
轴分别交于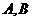 两点,若
两点,若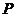 分线段
分线段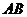 所成的
所成的
比为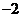 ,则直线
,则直线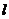 的方程为
.
的方程为
.
(1)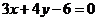 设
设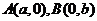 ,则
,则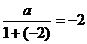 ,则
,则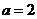 ;
;
且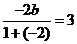 ,则
,则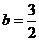 ,所以直线
,所以直线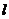 的方程为
的方程为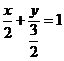 ,即
,即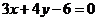 .
.
(2)已知点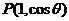 到直线
到直线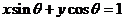 的距离等于
的距离等于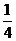 ,且
,且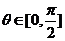 ,
,
则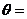 .
.
(2)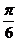
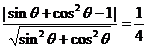 ,即
,即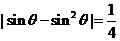 ,而
,而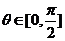 ,即
,即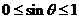 ,
,
得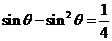 ,即
,即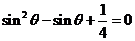 ,得
,得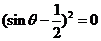 ,
,
即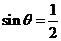 ,而
,而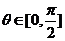 ,得
,得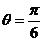 .
.
(3)如果直线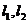 的斜率分别为方程
的斜率分别为方程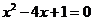 的两个根,则
的两个根,则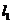 与
与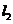 的夹角为 .
的夹角为 .
(3)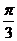 设斜率为
设斜率为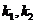 ,则
,则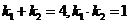 ,由夹角公式得
,由夹角公式得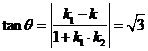 ,
,
又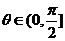 ,故
,故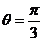 .
.
(4)已知两点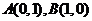 ,若直线
,若直线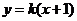 与线段
与线段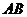 总有公共点,则
总有公共点,则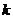 的取值
的取值
范围是 .
(4)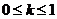
把直线化为一般式,即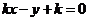 ,而两点
,而两点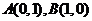 在直线上或在直线的
在直线上或在直线的
两侧,即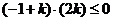 ,整理得
,整理得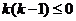 ,得
,得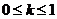 .
.
另外可以画图观察,直线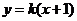 恒过定点
恒过定点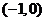 ,动直线满足与线段
,动直线满足与线段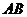
总有公共点,则最大的斜率为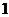 ,最小的斜率为
,最小的斜率为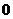 .
.
(5)已知直线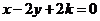 与两个坐标轴围成的三角形的面积不大于
与两个坐标轴围成的三角形的面积不大于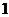 ,则
,则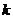 的取值
的取值
范围是 .
(5)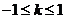 且
且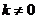 令
令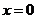 ,则
,则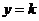 ;令
;令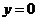 ,则
,则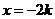 ,
,
故面积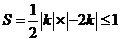 ,且
,且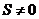 ,故
,故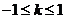 且
且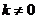 .
.
1.填空题
(1)经过点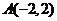 并且和两个坐标轴围成的三角形的面积是
并且和两个坐标轴围成的三角形的面积是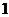 的直线方程
的直线方程
是( ).
A.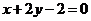 或
或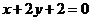 B.
B.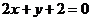 或
或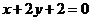
C.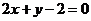 或
或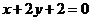 D.
D.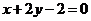 或
或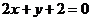
(1)D 该直线的斜率显然存在,设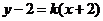 ,则该直线与
,则该直线与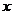 轴,
轴,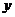 轴分别交于
轴分别交于
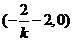 ,
,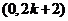 ,则三角形的面积是
,则三角形的面积是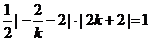 ,
,
得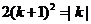 ,当
,当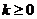 时,得
时,得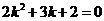 ,无解;
,无解;
当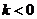 时,得
时,得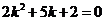 ,即
,即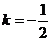 ,或
,或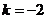 ,
,
得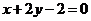 或
或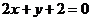 为所求.
为所求.
(2)过点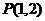 引直线,使
引直线,使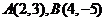 到它的距离相等,则这条直线的方程式
到它的距离相等,则这条直线的方程式
是( ).
A.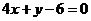 B.
B.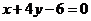
C.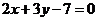 或
或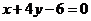 D.
D.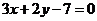 或
或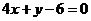
(2)D 该直线的斜率显然存在,设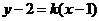 ,即
,即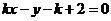 ,
,
则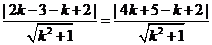 ,得
,得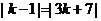 ,
,
即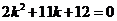 ,得
,得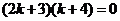 ,即
,即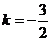 ,或
,或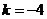 ,
,
得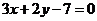 或
或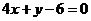 为所求.
为所求.
(3)当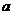 为任意实数时,直线
为任意实数时,直线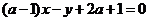 恒过的定点是( ).
恒过的定点是( ).
A.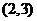 B.
B.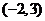 C.
C.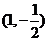 D.
D.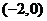
(3)B 由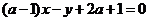 ,得
,得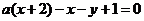 ,
,
由题意知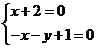 ,得
,得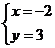 ,即过定点
,即过定点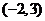 .
.
(4)若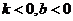 ,则直线
,则直线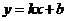 必不通过( ).
必不通过( ).
A.第Ⅰ象限 B.第Ⅱ象限 C.第Ⅲ象限 D.第Ⅳ象限
(4)A 若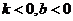 ,则直线
,则直线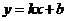 必通过第二、三、四象限,即不过第一象限.
必通过第二、三、四象限,即不过第一象限.
(5)过两点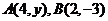 的直线的倾斜角是
的直线的倾斜角是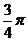 ,则
,则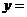 (
).
(
).
A.1 B.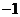 C.5 D.
C.5 D.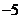
(5)D 直线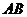 的斜率
的斜率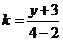 ,而该直线的倾斜角是
,而该直线的倾斜角是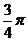 ,则
,则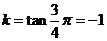 ,
,
得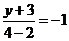 ,即
,即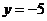 .
.
(6)已知两点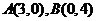 ,动点
,动点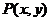 在线段
在线段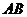 上运动,则
上运动,则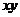 的最大值是( ).
的最大值是( ).
A.2 B.3 C.4 D.5
(6)B 表示线段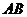 的方程为
的方程为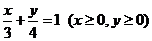 ,
,
而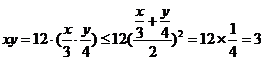 .
.
(7)若直线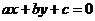 过第一、二、三象限,则( ).
过第一、二、三象限,则( ).
A.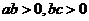 B.
B.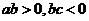 C.
C.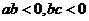 D.
D.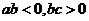
(7)C 由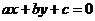 ,得
,得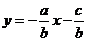 过第一、二、三象限,则
过第一、二、三象限,则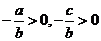 ,
,
得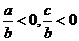 ,即
,即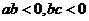 .
.
(8)若点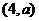 到直线
到直线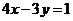 的距离不大于3,则
的距离不大于3,则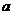 的取值范围是( ).
的取值范围是( ).
A.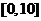 B.
B.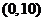 C.
C.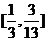 D.
D.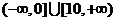
(8)A 由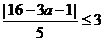 ,得
,得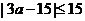 ,即
,即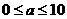 .
.
22.(本题满分12分)
已知点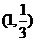 是函数
是函数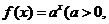 且
且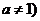 的图象上一点,等比数列
的图象上一点,等比数列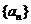 的前
的前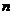 项和为
项和为
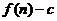 .数列
.数列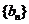
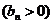 的首项为
的首项为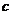 ,且前
,且前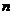 项和
项和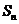 满足
满足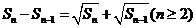 (Ⅰ)求数列
(Ⅰ)求数列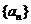 和
和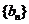 的通项公式 ;
的通项公式 ;
(Ⅱ)若数列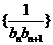 的前
的前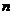 项和为
项和为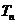 ,问满足
,问满足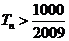 的最小正整数
的最小正整数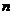 是多少?
是多少?
21.(本题满分12分)
已知函数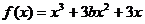 有极值点.
有极值点.
(Ⅰ)求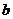 的取值范围;
的取值范围;
(Ⅱ)若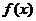 有两个极值点
有两个极值点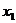 、
、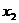 ,且
,且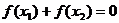 ,求
,求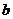 的值。
的值。
20. (本小题满分12分)
如图,四棱锥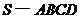 的底面
的底面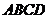 是正方形,侧面
是正方形,侧面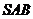 是等腰三角形且垂直于底面,
是等腰三角形且垂直于底面,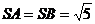 ,
,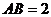 ,
,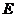 、
、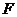 分别是
分别是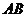 、
、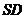 的中点.
的中点.
(Ⅰ)求证: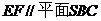 ;
;
(Ⅱ)求二面角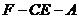 的大小.
的大小.
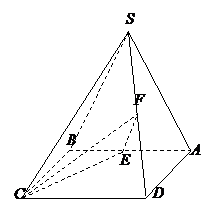
.
19.(本小题满分12分)
商家对某种商品进行促销活动,顾客每购买一件该商品就即刻抽奖.设每次抽奖中奖概率相同,且中奖比例及奖励额度如下:
|
奖励等级 |
一等奖 |
二等奖 |
|
所占比例 |
10% |
30% |
|
奖金数(元) |
100 |
20 |
一顾客购买该商品2件,求:
(Ⅰ)该顾客中奖的概率;
(Ⅱ)设该顾客获得的奖金数不小于100元的概率.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com